Sommaire
Déterminer graphiquement l’équation réduite d’une droite si c’est possible.
Méthode
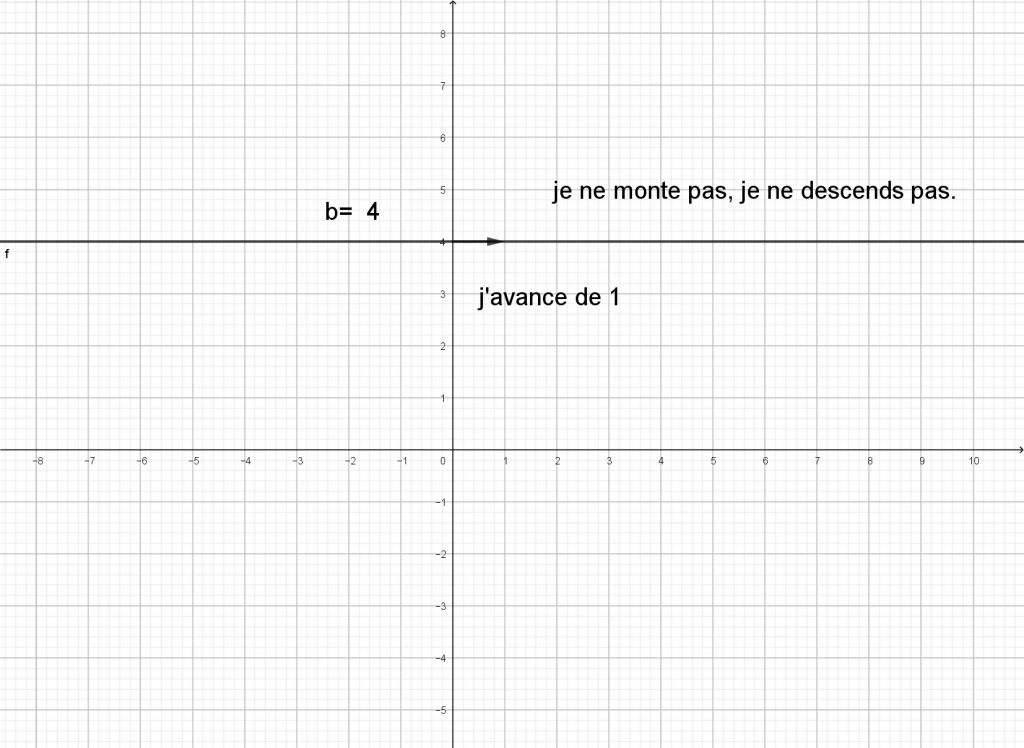
Je lis graphiquement l’ordonnée à l’origine sur l’axe des ordonnées. A partir de ce point, j’avance toujours horizontalement d’une graduation et verticalement je me déplace pour retomber sur la droite : si je monte ,le coefficient directeur est positif et si je descends le coefficient directeur est négatif.
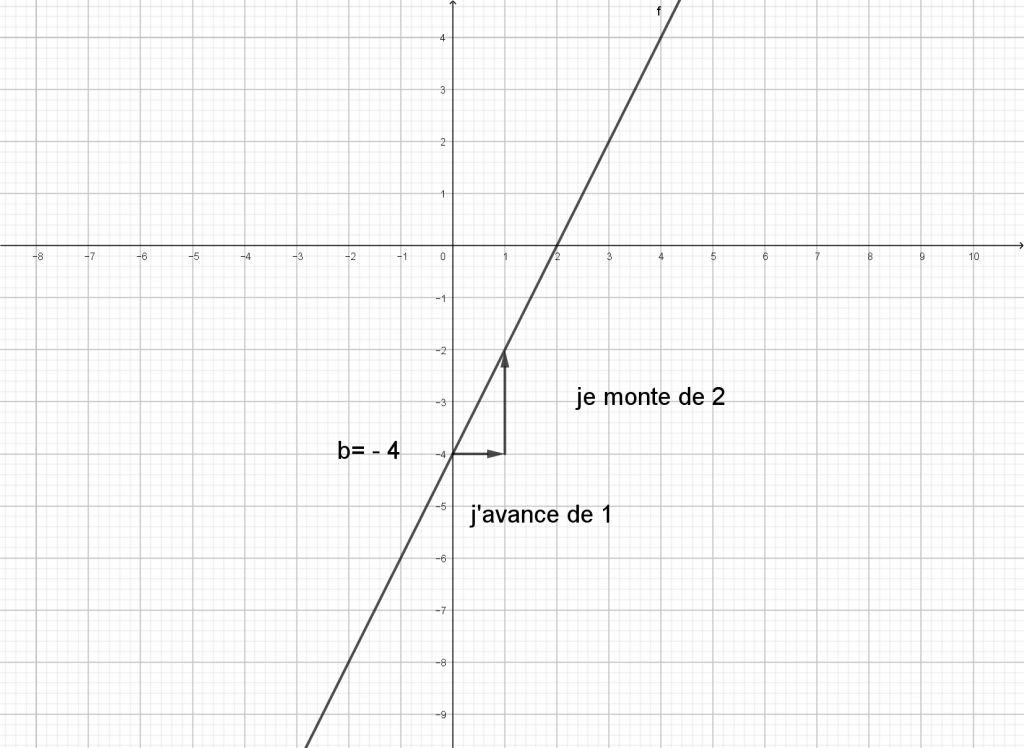
Exemple 1
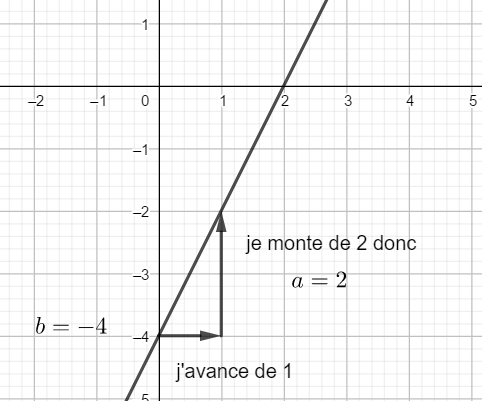
L’équation cherchée est donc y=2x-4
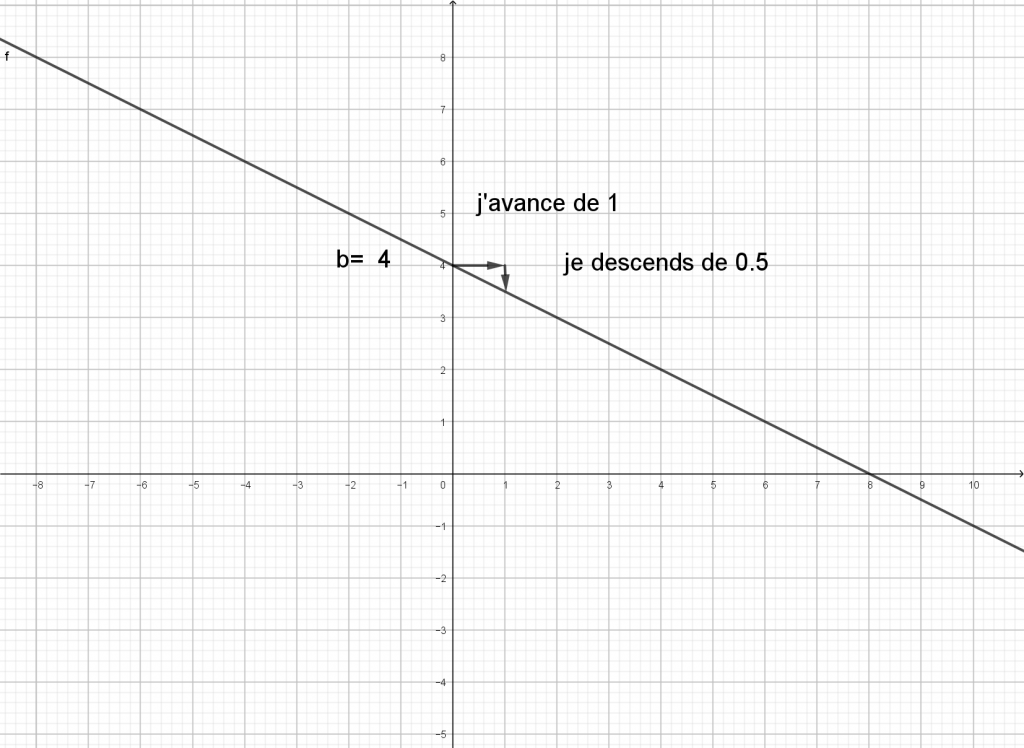
Exemple 2
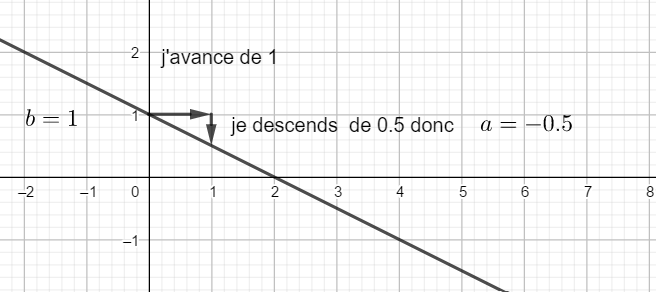
L’équation cherchée est donc y=-0.5x+1
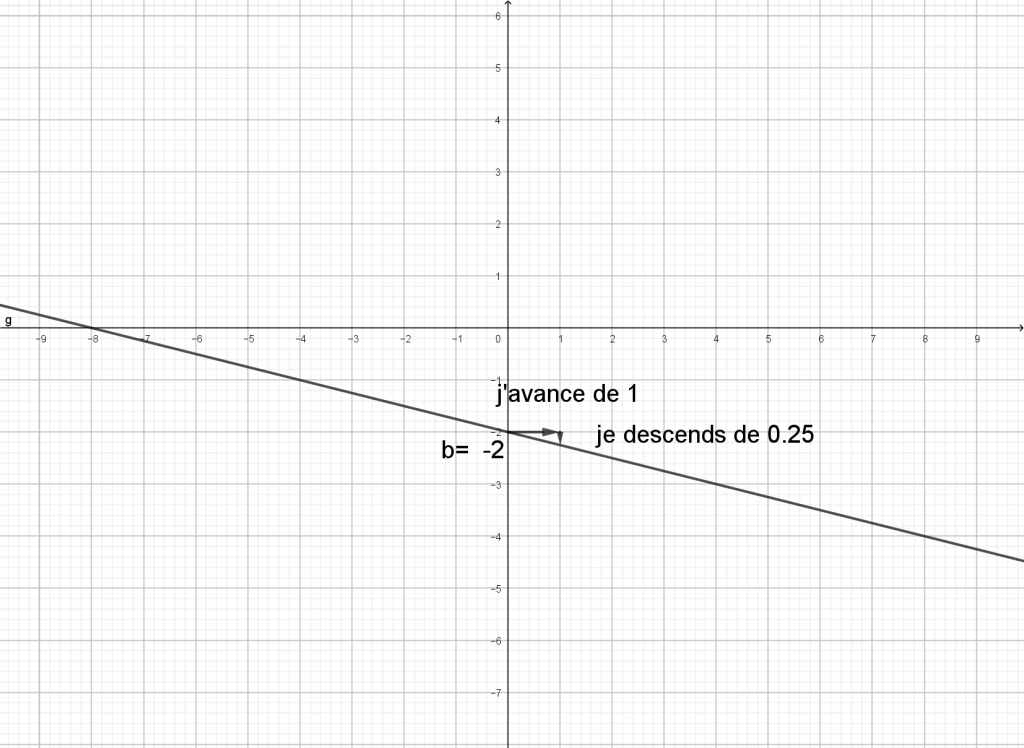
Exercice 1
Déterminer les équations réduites des droites ci-dessous, quand c’est possible.
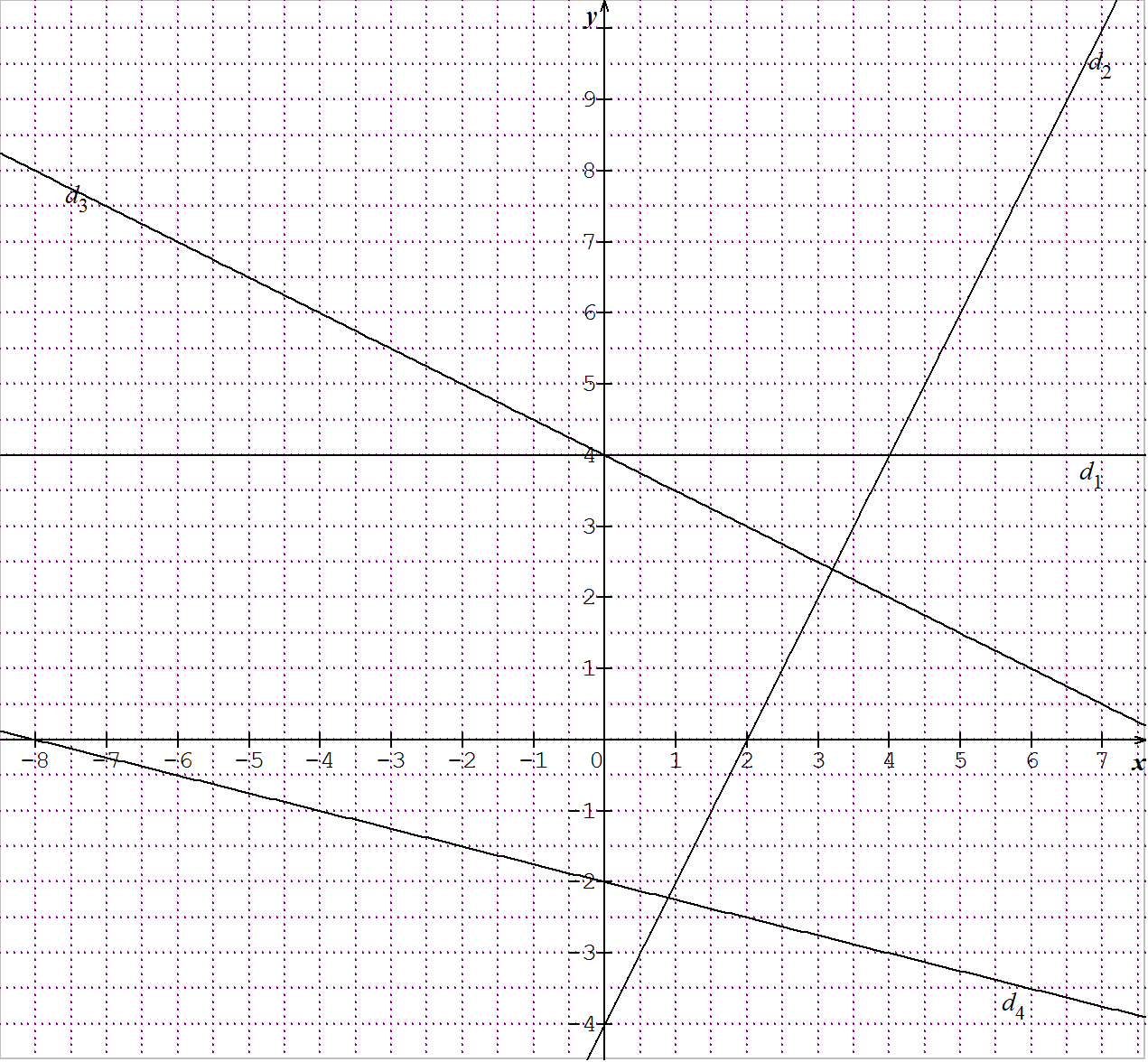
Déterminer par le calcul l’équation réduite d’une droite, si c’est possible.
Méthode
On note x_{A} et y_{A} les coordonnées du point A
On note x_{B} et y_{B} les coordonnées du point B
Si x_{A}= x_{B} alors la droite (AB) n’admet pas d’équation réduite.Tous les points de la droite ont des coordonnées qui vérifient x=x_{A}
Si x_{A}\neq x_{B} alors on calcule le coefficient directeur a=\frac{y_{B}-y_{A}}{x_{B}-x_{A}} et l’ordonnée à l’origine b=y_{A}-ax_{A}
Puis on remplace a et b par les résultats obtenus dans l’équation réduite y=ax+b
Remarque
Deux droites parallèles ont des coefficients directeurs égaux.
Exercice résolu
Déterminer l’équation réduite, si c’est possible, de la droite passant par les points A(2;4) et B(-1;0)
On n’hésite pas à repérer les coordonnées des points A et B ainsi
\hspace{0.4cm} x_{A} y_{A} \hspace{0.7cm} x_{B} y_{B}
\hspace{0.2cm} A(2;4) \hspace{0.4cm} B(-1;0)
Je compare x_{A} et x_{B}
\hspace{0.4cm} x_{A} \neq x_{B} car \hspace{0.4cm} 2 \neq -1
Je peux donc calculer le coefficient directeur , en utilisant la formule suivante:
\hspace{2cm} a=\frac{y_{B}-y_{A}} {x_{B}-x_{A}}On prend soin ensuite de remplacer les lettres par les bons nombres. Si le nombre est négatif, je prends l’habitude de l’écrire entre parenthèses.
\hspace{2cm} a=\frac{0-4} {(-1)-2} \\ \hspace{2cm} a=\frac{-4} {-3} \\ \hspace{2cm} a=\frac{4} {3}Je calcule ensuite l’ordonnée à l’origine, en utilisant la formule suivante:
\hspace{2cm} b= y_{A} – ax_{A}On prend soin ensuite de remplacer les lettres par les bons nombres. Si le nombre est négatif, je prends l’habitude de l’écrire entre parenthèses.
\hspace{2cm} b= y_{A} – ax_{A} \\ \hspace{2cm} b=4-(\frac{4}{3})\times2Pour effectuer ce calcul, on respecte la priorité des opérations. On commence par effectuer la multiplication : \hspace{2cm} b=4- \frac{4\times2}{3} \\ \hspace{2cm} b=4-\frac{8}{3}
Puis on effectue la somme 4- \frac{8}{3} . Pour cela on choisit un dénominateur commun , ici 3 . On multiplie ensuite le premier terme de la somme 4 par \frac {3}{3} :
\hspace{2cm} b=4 \times \frac{3}{3}- \frac{8}{3} \\ \hspace{2cm} b=\frac{12-8}{3} \\ \hspace{2cm} b=\frac{4}{3}Pour finir je remplace a et b par \frac{4} {3} et \frac{4} {3} dans l’équation réduite y=ax+b
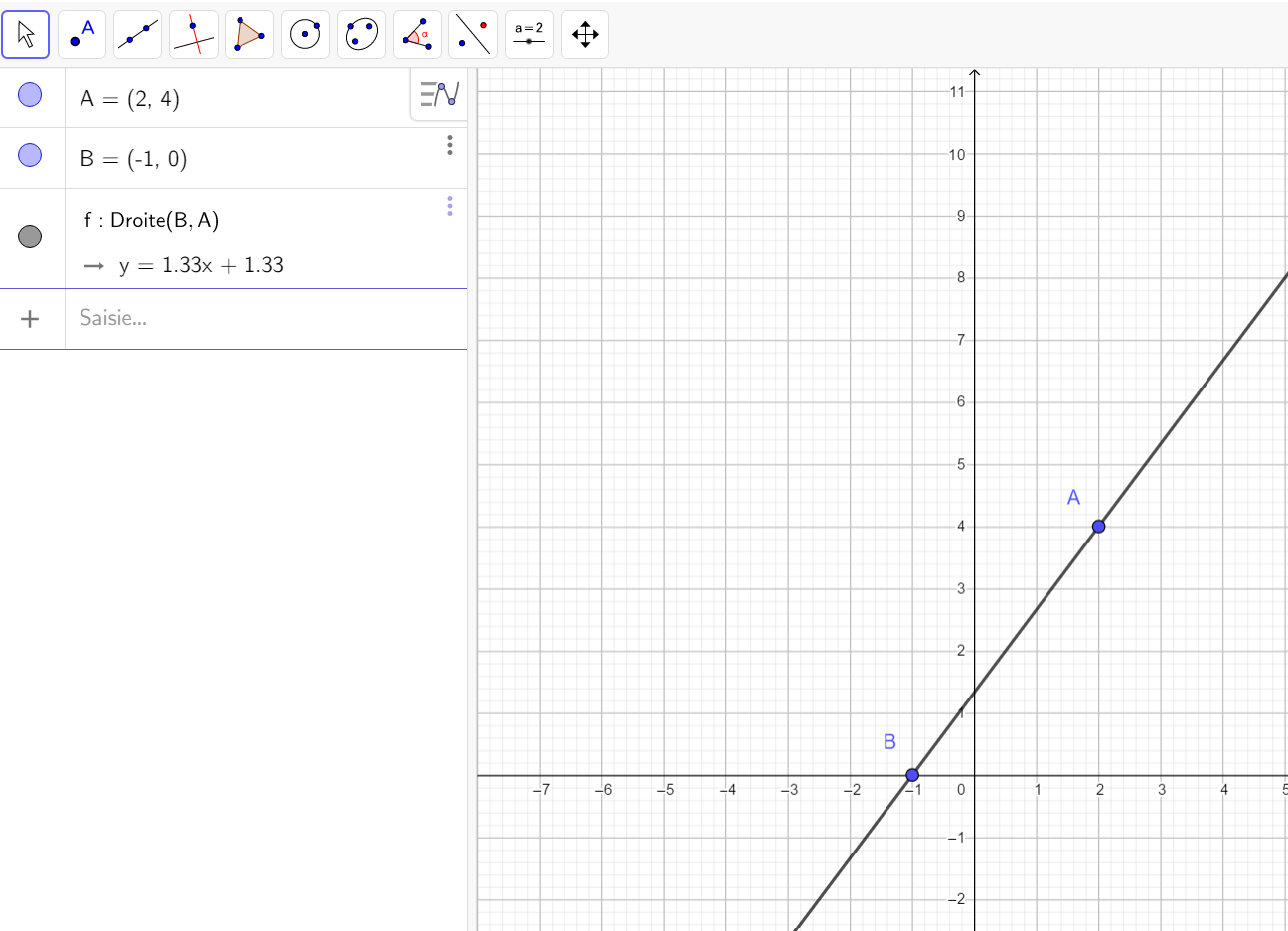
L’équation de la droite d est y= \frac{4} {3} x+ \frac{4} {3}
On valide la réponse à l’aide de Géogébra.
Exercice n°2
Déterminer l’équation réduite de d quand c’est possible.
On pourra utiliser Géogébra pour conjecturer l’équation réduite. Pour cela on crée deux points A et B dans le repère, on trace la droite qui passe par ces deux points et on lit son équation réduite dans la colonne algèbre. Dans la fenêtre ci-dessous tout est déjà configuré. Il ne reste qu’à cliquer sur le premier onglet en haut à gauche (le flèche) et sélectionner Déplacer dans le menu déroulant. Puis on déplace les points A et B pour obtenir ceux de l’énoncé . Par exemple dans la question 1 on a A(0;3) et B(5;-3). Ne pas hésiter à utiliser le 11ème onglet et sélectionner Déplacer graphique si nécessaire.
- d passe par A(0;3) et B(5;-3)
2. d passe par A(1;1) et B(-5;-2)
3. d passe par A(-3;5) et B(6;5)
4. d passe par A(1;-2) et B(1;3)
5. d passe par C(3;5) et a pour coefficient directeur 1
6. d passe par E(-2;0) et a pour coefficient directeur -2
7. d passe par E(-2;0) et est parallèle à la droite d’équation y=3x+8
Exercice n°3
Déterminer l’équation réduite de d quand c’est possible
1.d passe par A(5;2) et par B(5;3)
2. d passe par A(2;-2) et par B(6;-2)
3. d passe par A(0;-2) et B(5;-1).
4. d passe par les points A(10;-2) et par B(0;-3)
5. d passe par C(2;5) et a pour coefficient directeur -8
6. dpasse par E(-2;-4) et a pour coefficient directeur 1.
7. d passe par E(-2;7) et est parallèle à la droite d’équation y=x+8
8. d passe par E(1;0) et a pour ordonnée à l’origine 2