Sommaire
Exemples de résolution d’équations du second degré
La résolution d’équations du second degré en utilisant le discriminant est hors-programme. Seules certaines équations où une factorisation en produit de facteurs du premier degré est possible seront traitées.
Exemple n°1
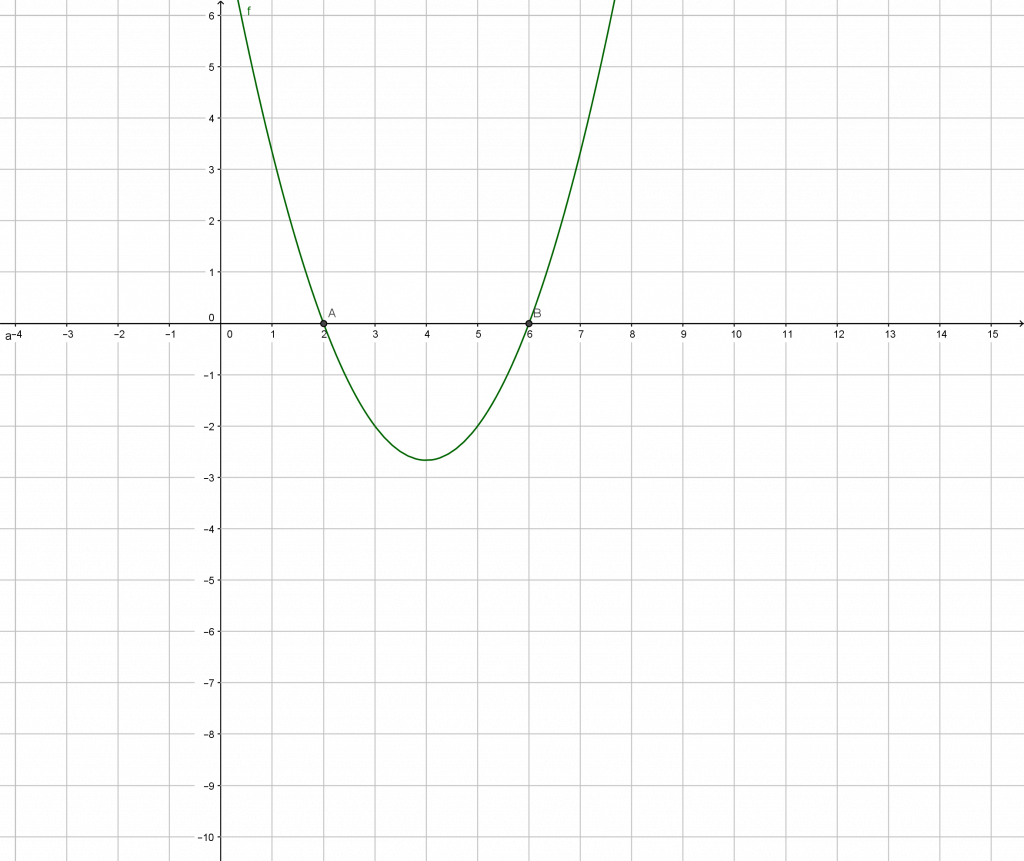
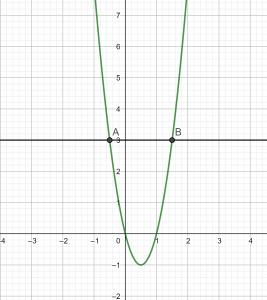
résoudre (2x-4)(\frac{1}{3}x-2)=0
Résoudre (2x-4)(\frac{1}{3}x-2)=0
C’est une équation du second degré car si on développait le produit nous obtiendrions un terme en x^{2}
Il n’est pas nécessaire de faire apparaître le zéro à droite, il y est déjà.
Il n’est pas nécessaire de factoriser le membre de gauche, c’est déjà un produit de facteurs du premier degré.
J’applique la règle du produit nul. Un produit est nul si le premier facteur est nul ou si le second facteur est nul.
2x-4=0 ou \frac{1}{3}x-2=0
Ce sont des équations du premier degré, il faut mettre à leur place les membres qui ne sont pas à leur place.
Dans la première équation -4 n’est pas à sa place, j’ajoute 4 de chaque côté.
Dans la seconde équation -2 n’est pas à sa place, j’ajoute 2 de chaque côté.
2x=4 ou \frac{1}{3}x=2
Dans la première équation le facteur 2 n’est pas à sa place, je divise par 2 de chaque côté
Dans la seconde équation le dénominateur 3 n’est pas à sa place, je multiplie par 3 de chaque côté.
x=\frac{4}{2} ou x={2}\times{3}\\x=2 ou x=6\\S=\{2;6\}
Remarque : pour vérifier que mes résultats sont justes, je peux montrer que si je remplace x par 2 l’égalité est vérifiée et pareil pour 6.
J’effectue d’abord ce qu’il y a entre parenthèses
({2}\times{2}-4)({\frac{1}{3}}\times{2}-2)=(4-4)(\frac{2}{3}-2)\\\hspace{3.5cm}=0l’égalité est vérifiée.
J’effectue d’abord ce qu’il y a entre parenthèses
({2}\times{6}-4)({\frac{1}{3}}\times{6}-2)=(12-4)(\frac{6}{3}-2)\\\hspace{3.5cm}={8}\times{(2-2)}\\\hspace{3.5cm}=0l’égalité est vérifiée.
Autre vérification avec Géogébra et son application Calcul Formel :
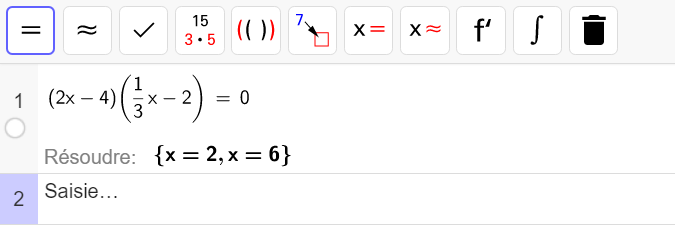
Exemple n°2
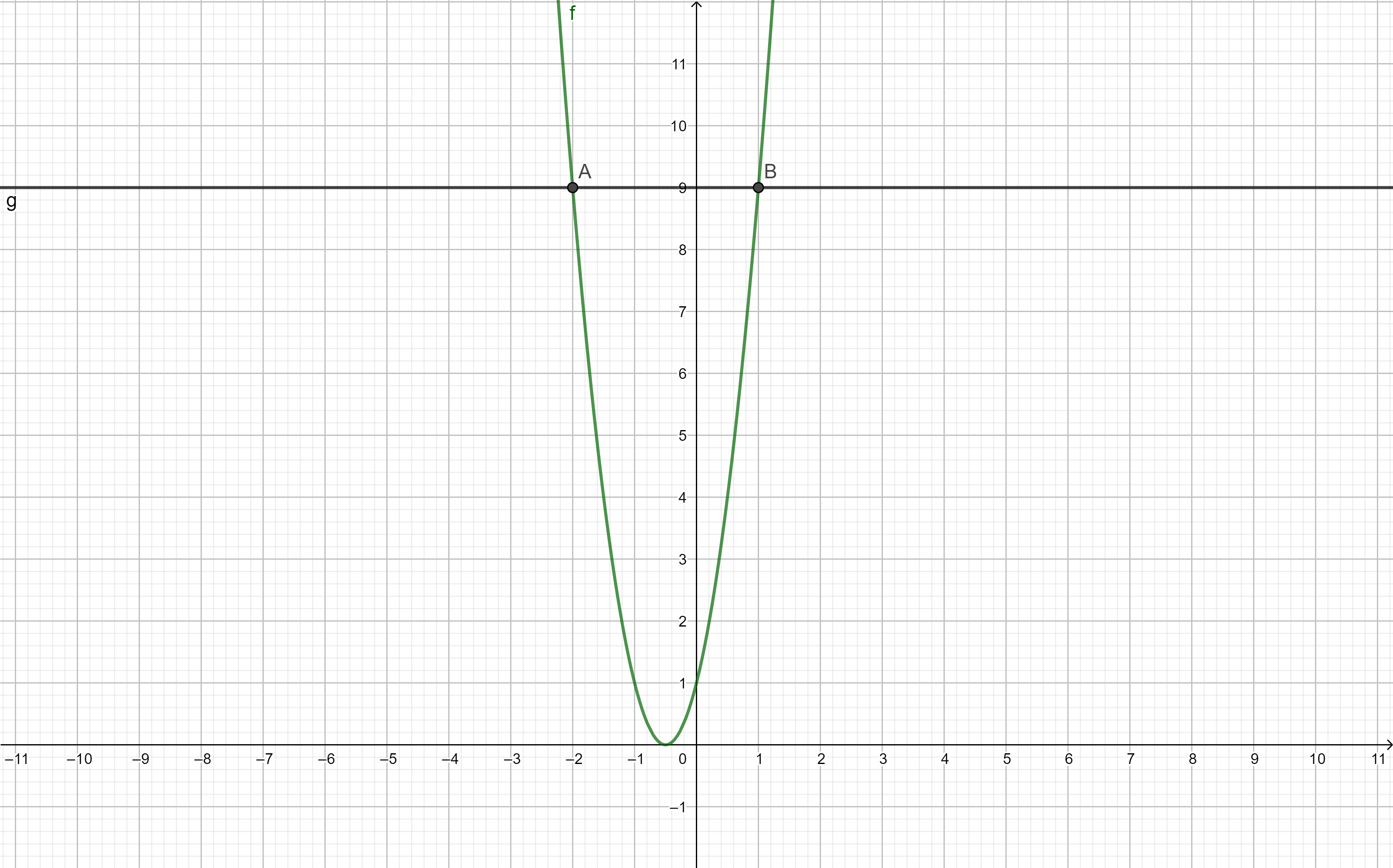
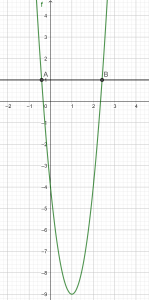
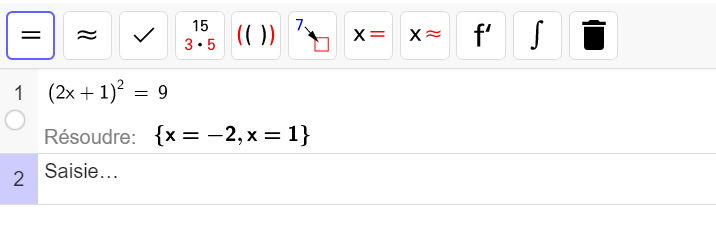
résoudre l’équation (2x+1)^{2}=9
L’équation à résoudre (2x+1)^{2}=9 est du 2nd degré car en développant (2x+1)^{2} le plus grand exposant de x est 2.
La méthode proposée concerne les équations du second degré.
(2x+1)^{2}=91.Je fais tout passer à gauche, zéro apparaît à droite.
le 9 à droite du signe égal n’est pas à sa place, j’enlève 9 de chaque côté.
(2x+1)^{2}-9=02. Je factorise le membre de gauche.
a. Il n’y a pas de facteur commun.
b. J’utilise l’identité remarquable a^{2}-b^{2}=(a-b)(a+b) pour factoriser (2x+1)^{2}-9\\a^{2}=(2x+1)^{2} \hspace{2cm}a=(2x+1)\\b^{2}=9\hspace{3.2cm}b=3
Je remplace a et b par (2x+1) et 3 dans a^{2}-b^{2}=(a-b)(a+b)\\(2x+1)^{2}-9=((2x+1)-3)((2x+1)+3)\\\hspace{2.1cm}=(2x-2)(2x+4)\\(2x-2)(2x+4)=0
3. J’applique la règle du produit nul : un produit de facteurs est nul si l’un de ses facteurs est nul.
Ici il y a deux facteurs (2x-2) ; (2x+4). Le premier facteur est nul ou le second facteur est nul.
(2x-2)=0 ou (2x+4)=0
Dans l’équation (2x-2)=0 le -2n’est pas à sa place, j’ajoute 2de chaque côté.
Dans l’équation (2x+4)=0 le 4 n’est pas à sa place, j’enlève 4 de chaque côté.
2x=2 ou 2x=-4
Dans l’équation 2x=2 le 2n’est pas à sa place, je divise par 2de chaque côté.
Dans l’équation 2x=-4 le 2 n’est pas à sa place, je divise par 2 de chaque côté.
x=\frac{2}{2} ou x=-\frac{4}{2}\\x=1 ou x=-2\\S=\{1;-2\}
Remarque : pour vérifier que mes résultats sont justes, je peux montrer que si je remplace x par 1 l’égalité est vérifiée et pareil pour -2.
J’effectue d’abord ce qu’il y a entre parenthèses.
Dans la parenthèse, je commence par le produit.
({2}\times{1}+1)^{2}=(2+1)^{2}Je fais la somme
\hspace{2cm}=3^{2}J’effectue la puissance
\hspace{2cm}=9L’égalité est vérifiée.
J’effectue d’abord ce qu’il y a entre parenthèses.
Dans la parenthèse, je commence par le produit.
({2}\times{(-2)}+1)^{2}=(-4+1)^{2}Je fais la somme
\hspace{2cm}=(-3)^{2}J’effectue la puissance
\hspace{2cm}=9L’égalité est vérifiée.
Autre vérification avec Géogébra et son application Calcul Formel :
Exemple n°3
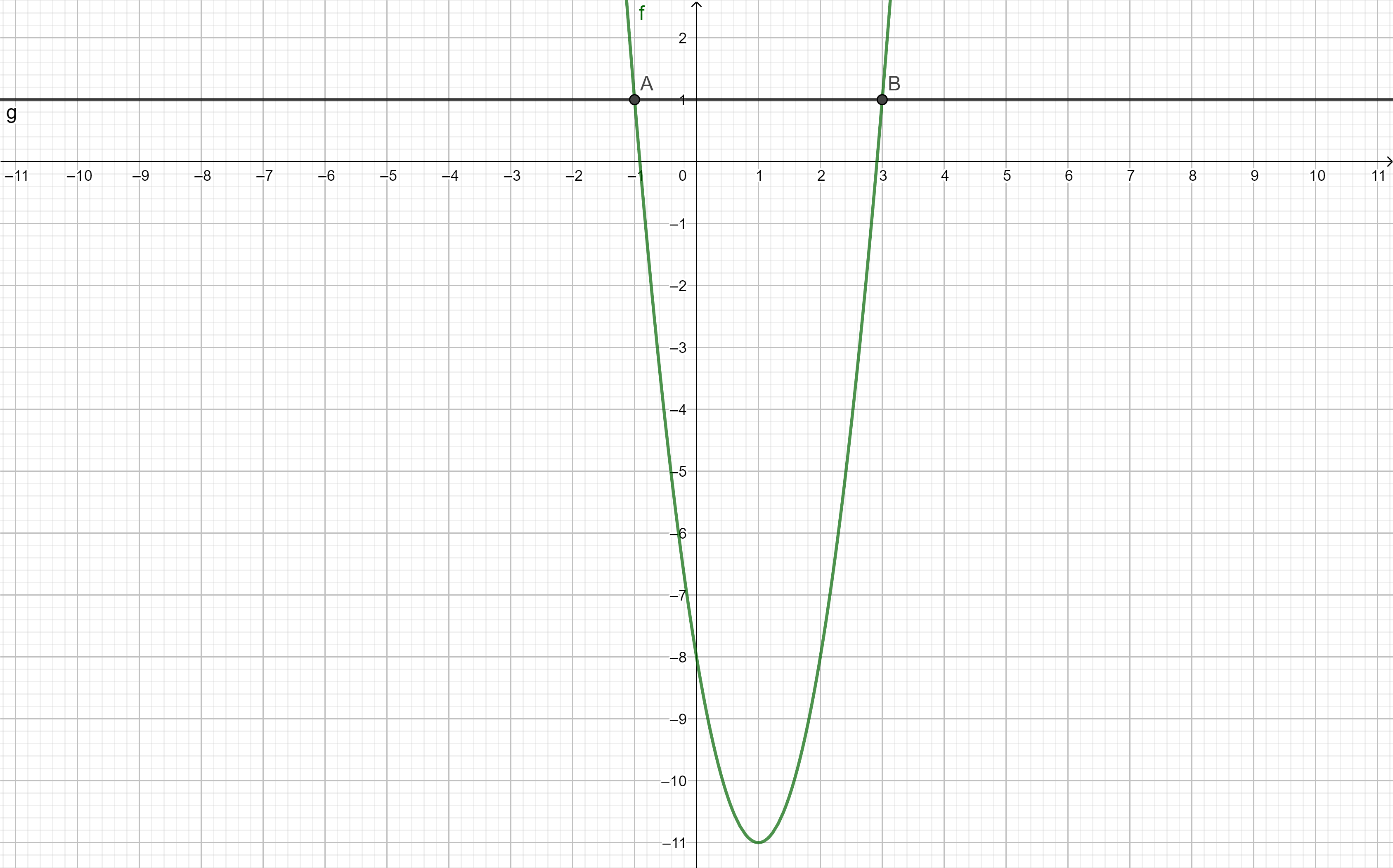
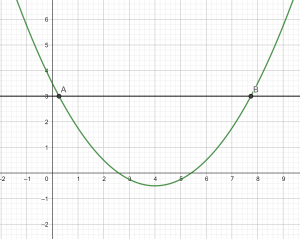
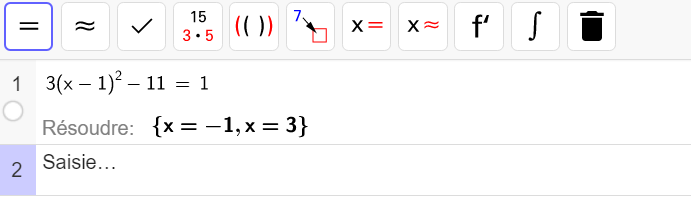
résoudre l’équation3(x-1)^{2}-11=1
L’équation à résoudre 3(x-1)^{2}-11=1 est du second degré car si on développe (x-1)^{2} le plus grand exposant de x est 2.
La méthode proposée concerne les équations du second degré.
3(x-1)^{2}-11=11.Je fais tout passer à gauche, zéro apparaît à droite.
1 n’est pas à sa place, j’enlève 1 de chaque côté.
3(x-1)^{2} -11-1=0\\3(x-1)^{2}-12=02. Je factorise le membre de gauche.
a. Il y a un facteur commun.
J’écris 3(x-1)^{2}={3}\times{(x-1)^{2}}\\\hspace{1.8cm}12={3}\times{4}
Je mets 3 en facteur.
3[(x-1)^{2}-4]=0b. J’utilise l’identité remarquable a^{2}-b^{2}=(a-b)(a+b) pour factoriser (x-1)^{2}-4\\a^{2}=(x-1)^{2} \hspace{2cm}a=(x-1)\\b^{2}=4\hspace{3.2cm}b=2
Je remplace a et b par (x-1) et 2 dans a^{2}-b^{2}=(a-b)(a+b)\\(x-1)^{2}-4=((x-1)-2)((x-1)+2)\\\hspace{2.1cm}=(x-3)(x+1)\\3(x-3)(x+1)=0
3. J’applique la règle du produit nul : un produit de facteurs est nul si l’un de ses facteurs est nul.
Ici il y a trois facteurs 3 ; (x-3) ; (x+1). Le premier n’est pas nul, seuls le second et le troisième peuvent l’être.
(x-3)=0 ou (x+1)=0\\x=3 ou x=-1\\S=\{-1;3\}
Remarque : pour vérifier que mes résultats sont justes, je peux montrer que si je remplace x par -1 l’égalité est vérifiée et pareil pour 3.
J’effectue d’abord ce qu’il y a entre parenthèses
3((-1)-1)^{2}-11={3}\times{(-2)^{2}}-11J’effectue les puissances ( ici les carrés)
\hspace{2.8cm}={3}\times{4}-11J’effectue le produit :
\hspace{2.8cm}=12-11Je fais la différence
\hspace{2.8cm}=1l’égalité est vérifiée.
J’effectue d’abord ce qu’il y a entre parenthèses
3(3-1)^{2}-11={3}\times{(2)^{2}}-11J’effectue les puissances ( ici les carrés)
\hspace{2.8cm}={3}\times{4}-11J’effectue le produit :
\hspace{2.8cm}=12-11Je fais la différence
\hspace{2.8cm}=1l’égalité est vérifiée.
Autre vérification avec Géogébra et son application Calcul Formel :
Exercice
résoudre les équations suivantes dans R
a) (3x-9)(-5x+1)=0
b)(x-3)(-3x+5)=0
c)(\frac{2}{3}x-4)(x-2)=0
d) (x-2)^{2}-6=3
e) (2x-1)^{2}-1=3
f) (\frac{x}{2}-2)^{2}-\frac{1}{2}=-\frac{1}{4}
g) 5(x-1)^{2}-9=1
Utiliser la fenêtre de Calcul Formel ci-dessous pour valider vos réponses.