logo

2.Coordonnées d’un point. Milieu. Distance. Cours.

Sommaire

Coordonnées d’un point dans un repère.

Rappels

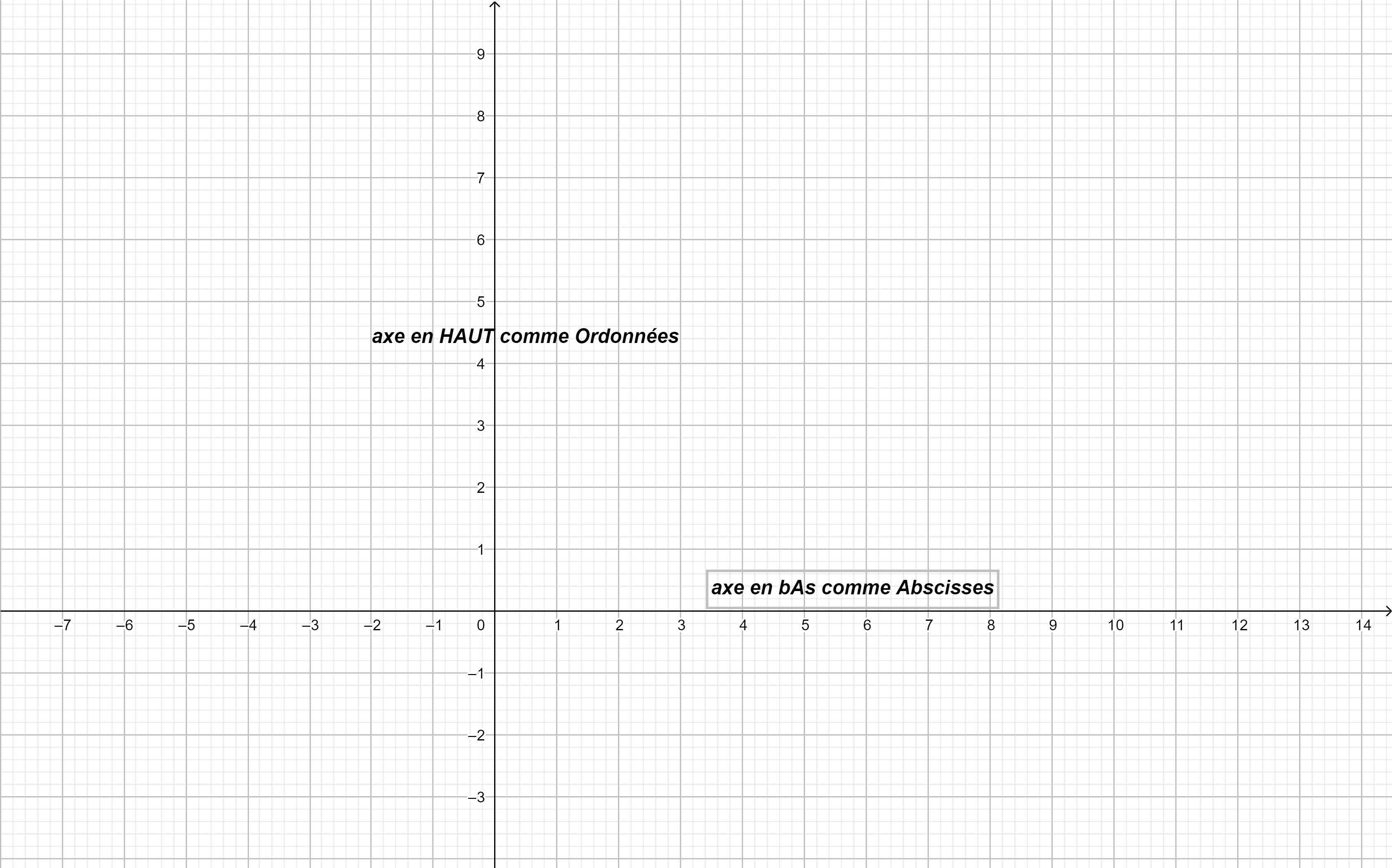
Pour représenter le plan en géométrie analytique, on a besoin de définir deux axes: l’axe des abscisses et l’axe des ordonnées, et dont le point d’intersection s’appelle l’origine et se note généralement O.

Ces deux axes peuvent être perpendiculaires (on parle alors de repère orthogonal) ou pas.

Sur chacun de ces axes, on définit une unité, qui peut avoir la même longueur (repère normé) ou non.

La plupart du temps, on utilise un repère orthonormé (ou orthonormal), c’est à dire un repère à axes

perpendiculaires (orthogonaux) et portant la même longueur comme unité (« normés »)

Question n°1 

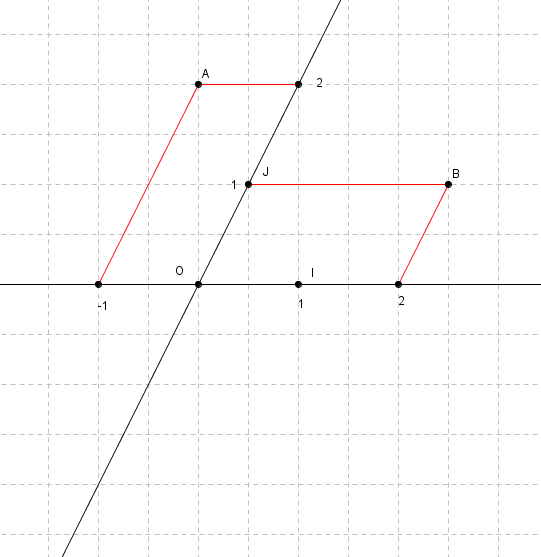
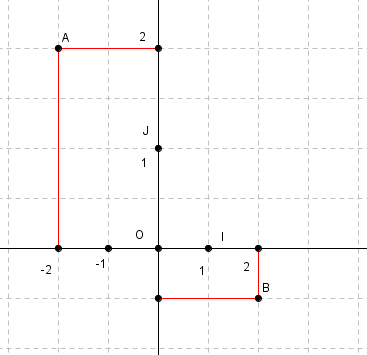
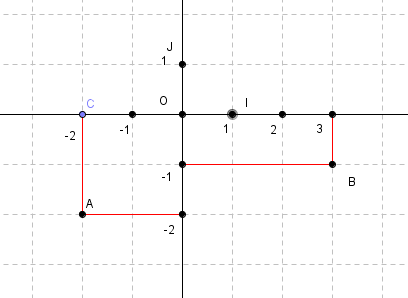
 Dans chaque cas, déterminer les coordonnées des points A et B dans le repère proposé.

cas n°1:

cas n°2:

cas n°3:

aide
correction

Exercice n°1 

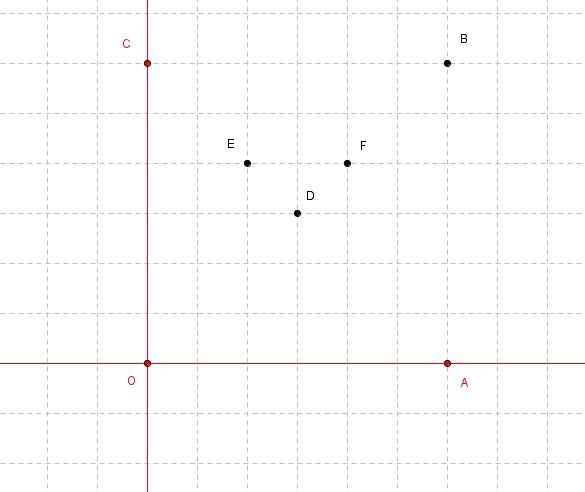
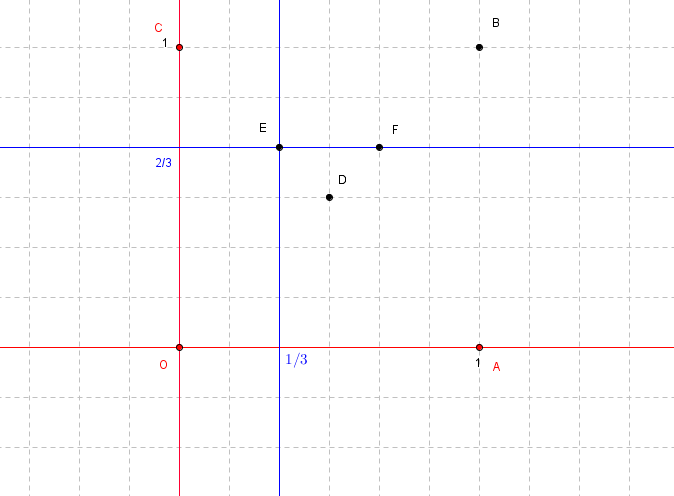
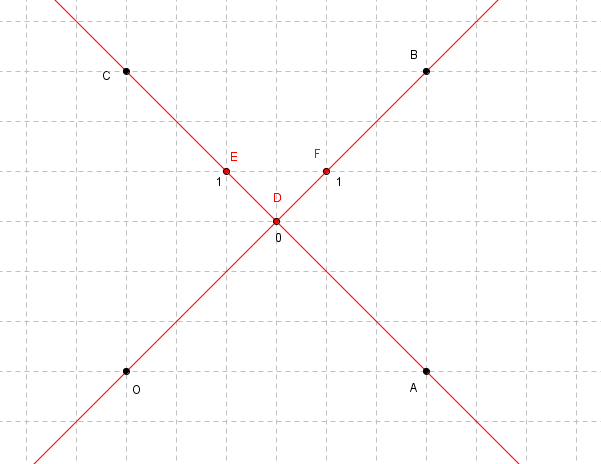
On a placé les points suivants dans le quadrillage ci-dessous.

1) Déterminer les coordonnées des points dans le repère (O,A,C)

correction

2) Déterminer les coordonnées des points dans le repère (D,F,E)

correction

 Coordonnées du milieu de deux points.

Propriété

A(x_A;y_A) B(x_B;y_B)  

Si I est le milieu de [AB] alors x_I=\frac{x_A+x_B}{2} et y_I=\frac{y_A+y_B}{2} 

Exercice n°2

 Déterminer par le calcul, les coordonnées du point I le milieu de [AB] .

On peut conjecturer les coordonnées du milieu I en utilisant la fenêtre géogébra ci-dessous. Pour cela on déplacera les points A et B jusqu’à obtenir les points donnés dans les questions en cliquant sur le premier onglet ( la flèche) et en sélectionnant Déplacer dans le menu déroulant. On n’hésitera pas à bouger le repère en cliquant sur le 11ème onglet et en sélectionnant Déplacer graphique dans le menu déroulant.

  1. A(1;1) et B(3;-1) 
correction

2. A(5;3) et B(-1;6) 

correction

3. A(1;\frac{2}{3}) et B(\frac{1}{5};-1) 

correction

Exercice n°3

Soient les points B(-1;3) et C(-2;0) 

 Déterminer par le calcul, les coordonnées de I , le centre du cercle de diamètre [BC] .

Avant de commencer les calculs, on peut placer les points dans la fenêtre Géogébra ci-dessous.

Pour placer les points, on clique sur le deuxième onglet en haut en partant de la gauche et on sélectionne Point dans le menu déroulant. Puis dans le repère on clique gauche pour placer les deux points. On n’hésite pas à renommer les points, pour cela on clique droit sur chaque point, on sélectionne Renommer dans le menu déroulant et on tape B puis C.

On peut aussi saisir dans la colonne de gauche B=(-1,3) et C=(-2,0).Attention il faut séparer les nombres par une virgule.

Pour déterminer le milieu, on clique gauche sur le deuxième onglet en haut en partant de la gauche et on sélectionne Milieu ou centre dans le menu déroulant.Puis dans le repère, on clique sur A et B. On n’hésite pas à renommer le milieu, pour cela on clique droit sur le milieu, on sélectionne Renommer dans le menu déroulant et on tape I.

correction

Exercice n°4 

Soient les points B(2;-1) et I(3;7) 

 Déterminer par le calcul, les coordonnées de C, tel que I  soit le milieu de [BC]  .

Vous pouvez vous inspirer de la vidéo ci-dessous.

correction

Exercice n°5

A(1;1) ,B(5;3) et C(\frac{7}{2};0) 

On note I le milieu [AC] .

1) Déterminer par le calcul les coordonnées du point I milieu de [AC].

correction

2) Déterminer par le calcul les coordonnées du point D tel que I soit le milieu de [BD].

correction

3) Quelle est la nature du quadrilatère  ABCD ? Justifier votre réponse.

correction

 Distance entre deux points.

propriété

\hspace{1cm}A(x_A;y_A) B(x_B;y_B)  

AB=\sqrt {{(x_B-x_A) }^{2}+{(y_B-y_A) }^{2}}

Exercice n°6 : 

Déterminer par le calcul la distance AB  dans chaque cas.

On peut conjecturer la distance AB en utilisant la fenêtre géogébra ci-dessous. Pour cela on déplacera les points A et B en cliquant sur le premier onglet ( la flèche) et en sélectionnant Déplacer dans le menu déroulant. On n’hésitera pas à bouger le repère en cliquant sur le 11ème onglet et en sélectionnant Déplacer graphique dans le menu déroulant.

Remarque: s’il est difficile de bien placer un point, on peut sélectionner l’une ou les deux coordonnées , taper les coordonnées et valider avec enter au clavier de l’ordinateur.

  1. A(1;1) et B(-3;-1) 
correction

2. A(-1;2) et B(-3;-4) . 

correction

3. A(1;\frac{2}{3}) et B(\frac{1}{5};-1) 

correction

Exercice n°7 

1) Déterminer par lecture graphique les coordonnées des points  A, B, C et D dans le repère orthonormé ci-dessus.

correction

2) Calculer les distances AB, BC, DC et DA. 

Pour pouvoir conjecturer ces distances, il faut cliquer sur les trois barres à droite, sélectionner Affichage dans le menu déroulant et enfin cocher la case Algèbre.

Pour déterminer la distance AB, on clique gauche sur le huitième onglet en haut en partant de la gauche et on sélectionne Distance ou longueur dans le menu déroulant.Puis dans le repère, on clique gauche sur A et B

correction AB
correction BC
correction DC
correction DA

3) En déduire la nature du quadrilatère ABCD.

correction

Exercice n°8 

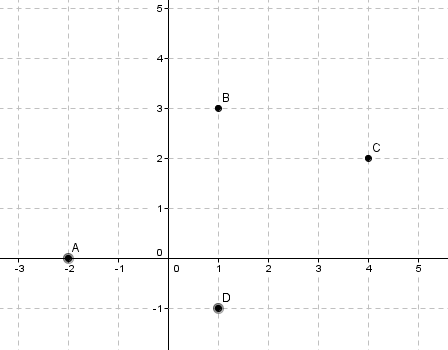
Soient quatre points du plan A(-2;0) , B(1;3)  , C(4;2) et D(1;-1)  

1) Placer les points dans le repère orthonormé ci-dessous.

  1. Placer les points A, B, C, D dans le repère.
correction

2) Calculer les distances AB, BC, CD et DA

Avant de commencer les calculs, on peut utiliser la  fenêtre Géogébra ci-dessus pour conjecturer les résultats.

Pour déterminer la distance AB, on clique gauche sur le huitième onglet en haut en partant de la gauche et on sélectionne Distance ou longueur dans le menu déroulant.Puis dans le repère, on clique gauche sur A et B

correction AB
correction BC
correction CD
correction DA

3) En déduire la nature du quadrilatère ABCD.

correction

Exercice n°9

 Déterminer les coordonnées du centre du cercle de diamètreAB et son rayon pour A(-2;5) , B(1;3)

Avant de commencer les calculs, placer A et B dans la fenêtre Géogébra ci-dessous pour conjecturer les résultats.

correction du centre
correction du rayon

©2020 – Math’O karé SAS

Certains élèves ont du mal à différencier abscisse et ordonnée.

L’initiale de abscisse est a, l’initiale de ordonnée est o. Dans l’alphabet le a est placé avant le o. Ainsi l’abscisse est la première coordonnée et l’ordonnée est la seconde.

Si on a A(-8;1) , la première coordonnée -8 est l’abscisse de A et la seconde coordonnée 1 est l’ordonnée de A. Pour les axes, il suffit de regarder la figure ci-dessous.

coordsaide
A(-1;2) B(2;1)
A(-2;2) B(2;-0.5)
A(-2;-2) B(3;-1)
2.coordonnées1correction
2.coordonnées2correction
2.coordonnées3correction

1) Lire graphiquement les coordonnées des points de la figure dans le repère

2.coordonnéesexo1correction1

Dans le repère   (O,A,C), par définition, les points du repère ont pour coordonnées : O(0,0), A(1;0) et C(0;0)

Je détermine graphiquement les coordonnées du point E.

Je trace la parallèle à l’axe des ordonnées (OC) passant par E, cette droite coupe l’axe des abscisses (OA)  et  x_{E}=\frac{1}{3}. Je trace la parallèle à l’axe des abscisses (OA)  passant par E, cette droite coupe l’axe des ordonnées (OC)   et  y_{E}=\frac{2}{3}.

Donc, dans le repère  (O,A,C), E(\frac{1}{3};\frac{2}{3})

2.coordonnéesexo1correction1bis

De façon analogue, on montre que  dans le repère  (O,A,C), D(\frac{1}{2};\frac{1}{2}) , F(\frac{2}{3};\frac{2}{3}) et B (1;1) 

 Lire graphiquement les coordonnées des points de la figure dans le repère (D,F,E)

Dans le repère (D,F,E), par les points du repère ont , par définition, les coordonnées suivantes:

D(0;0) , F(1;0) et E(0;1) 

2.coordonnéesexo1.2png

De façon analogue à la question 1) on détermine graphiquement les coordonnées des autres points.

A(0;-3) , B(3;0) , C(0;3) et  O(-3;0) 

On n’hésite pas à repérer les coordonnées des points A et B ainsi

\hspace{0.6cm} x_{A} y_{A} \hspace{0.6cm} x_{B} y_{B}

\hspace{0.2cm} A(1;1) \hspace{0.4cm} B(-3;-1)

On écrit la formule du cours :

x_I=\frac {x_A+x_B}{2}\hspace {2cm}y_I=\frac {y_A+y_B}{2}

Et on prend soin de bien remplacer les lettres par les bons nombres. Dans le cas d’un nombre négatif, on le met entre parenthèses.

x_I=\frac {1+3}{2}\hspace {2cm}y_I=\frac {1+(-1)}{2}

On calcule. Si vous utilisez la calculatrice , tapez cette séquence de calcul (1+3)/2 en utilisant les parenthèses « invisibles  » qui entourent le numérateur. Si vous tapez 1+3/2, vous obtiendrez 2.5 car la machine calculera 3/2 en priorité ce qui est faux

x_I=\frac {4}{2}\hspace {2cm}y_I=\frac {0}{2}

x_I=2\hspace {2cm}y_I=0

Donc I(2;0)

On n’hésite pas à repérer les coordonnées des points A et B ainsi

\hspace{0.6cm} x_{A} y_{A} \hspace{0.6cm} x_{B} y_{B}

\hspace{0.2cm} A(5;3) \hspace{0.4cm} B(-1;6)

On écrit la formule du cours :

x_I=\frac {x_A+x_B}{2}\hspace {2cm}y_I=\frac {y_A+y_B}{2}

Et on prend soin de bien remplacer les lettres par les bons nombres. Dans le cas d’un nombre négatif, on le met entre parenthèses.

x_I=\frac {5+(-1)}{2}\hspace {2cm}y_I=\frac {3+6}{2}

On calcule. Si vous utilisez la calculatrice , tapez cette séquence de calcul (5+(-1))/2 en utilisant les parenthèses « invisibles  » qui entourent le numérateur. Si vous tapez 5+(-1)/2, vous obtiendrez 4.5 car la machine calculera (-1)/2 en priorité ce qui est faux

x_I=\frac {4}{2}\hspace {2cm}y_I=\frac {9}{2}

x_I=2\hspace {2cm}y_I=\frac {9}{2}

Donc I(2;\frac {9}{2})

On n’hésite pas à repérer les coordonnées des points A et B ainsi

\hspace{0.6cm} x_{A} y_{A} \hspace{0.6cm} x_{B} y_{B}

\hspace{0.2cm} A(1;\frac{2}{3}) \hspace{0.4cm} B(\frac{1}{5};-1)

On écrit la formule du cours :

x_I=\frac {x_A+x_B}{2}\hspace {2cm}y_I=\frac {y_A+y_B}{2}

Et on prend soin de bien remplacer les lettres par les bons nombres. Dans le cas d’un nombre négatif, on le met entre parenthèses.

x_I=\frac {1+\frac{1}{5}}{2}\hspace {2cm}y_I=\frac {\frac{2}{3}+(-1)}{2}

On calcule 1+\frac{1}{5}.Il faut mettre les deux fractions au même dénominateur, ici 5. Pour cela, on multiplie le premier membre 1 par 5, en haut et en bas.

On calcule \frac{2}{3}-1. Il faut mettre les deux fractions au même dénominateur, ici 3. Pour cela, on multiplie le second membre 1 par 3, en haut et en bas.

x_I=\frac {\frac{5}{5}+\frac{1}{5}}{2}\hspace {2cm}y_I=\frac {\frac{2}{3}-\frac{3}{3}}{2}

x_I=\frac {\frac{6}{5}}{2}\hspace {2cm}y_I=-\frac{\frac {1}{3}}{2}

Pour calculer \frac{\frac{6}{5}}{2}, j’applique la règle suivante : diviser par une fraction revient à multiplier par son inverse

x_I= {\frac{6}{5}}\times{\frac{1}{2}}\hspace {2cm}y_I=-{\frac {1}{3}}\times{\frac{1}{2}}

Avant de calculer {\frac{6}{5}}\times{\frac{1}{2}} mieux vaut simplifier en haut et en bas par 2, en effet 6 et 2 sont divisibles par 2.

x_I=\frac{3}{5}\hspace {2cm}y_I=-\frac{1}{6}

Donc I(\frac{3}{5};-\frac{1}{6})

On n’hésite pas à repérer les coordonnées des points B et C ainsi

\hspace{0.6cm} x_{B} y_{B} \hspace{0.6cm} x_{C} y_{C}

\hspace{0.2cm} B(-1;3) \hspace{0.4cm} C(-2;0)

On écrit la formule du cours :

x_I=\frac {x_B+x_C}{2}\hspace {2cm}y_I=\frac {y_B+y_C}{2}

Et on prend soin de bien remplacer les lettres par les bons nombres. Dans le cas d’un nombre négatif, on le met entre parenthèses.

x_I=\frac {(-1)+{-2}}{2}\hspace {2cm}y_I=\frac {3+0}{2}

On calcule. Si vous utilisez la calculatrice , tapez cette séquence de calcul (3+0)/2 en utilisant les parenthèses « invisibles  » qui entourent le numérateur. Si vous tapez 3+0/2, vous obtiendrez 3 car la machine calculera 0/2 en priorité ce qui est faux

x_I=-\frac {3}{2}\hspace {2cm}y_I=\frac {3}{2}

 

Donc I(-\frac {3}{2};\frac {3}{2})

Tout d’abord, on ne cherche pas les coordonnées du milieu mais celles d’un des points. Ici le point C. Comme on ne connaît pas ses coordonnées, on les remplace par les lettres x et y.

On pose C(x;y)

On n’hésite pas à repérer les coordonnées des points B ,  C et I ainsi

\hspace{0.6cm} x_{B} y_{B} \hspace{0.6cm} x_{C} y_{C} \hspace{0.6cm} x_{I} y_{I}

\hspace{0.2cm} B(2;-1) \hspace{0.4cm} C(x;y) \hspace{0.4cm} I(3;7)  

On écrit la formule du cours :

x_I=\frac {x_B+x_C}{2}\hspace {2cm}y_I=\frac {y_B+y_C}{2}

Et on prend soin de bien remplacer les lettres par les bons nombres. Dans le cas d’un nombre négatif, on le met entre parenthèses.

3=\frac {2+x}{2}\hspace {2cm}7=\frac {(-1)+y}{2}

Nous avons deux équations du premier degré à résoudre. La première 3=\frac {2+x}{2} qu’on peut aussi écrire \frac {2+x}{2}=3.

Le 2 au dénominateur n’est pas à sa place, je multiplie par 2 de chaque côté de l’égalité.

2+x={3}\times{2}

2+x=6

Le 2 à gauche n’est pas à sa place, c’est un terme dans une somme. Le contraire d’ajouter 2 est enlever 2.

J’enlève 2 de chaque côté 

x=6-2

x=4

 

La seconde 7=\frac {(-1)+y}{2} qu’on peut aussi écrire \frac {(-1)+y}{2}=7.

Le 2 au dénominateur n’est pas à sa place. Le contraire de diviser par 2 est multiplier par 2.Je multiplie par 2 de chaque côté de l’égalité.

(-1)+y={7}\times{2}

-1+y=14

Le -1 à gauche n’est pas à sa place, c’est un terme dans une somme. Le contraire d’enlever 1  est ajouter 1.

J’ajoute 1 de chaque côté 

y=14+1

y=15

2+x=6\hspace {2cm} -1+y=14

x=6-2\hspace {3cm}y=14+1

x=4\hspace {3.5cm}y=15

 

Donc C(4;15)

On n’hésite pas à repérer les coordonnées des points A et C ainsi

\hspace{0.6cm} x_{A} y_{A} \hspace{0.6cm} x_{C} y_{C}

\hspace{0.2cm} A(1;1) \hspace{0.4cm} C(\frac{7}{2};0)

On écrit la formule du cours :

x_I=\frac {x_A+x_C}{2}\hspace {2cm}y_I=\frac {y_A+y_C}{2}

Et on prend soin de bien remplacer les lettres par les bons nombres. Dans le cas d’un nombre négatif, on le met entre parenthèses.

x_I=\frac {1+\frac{7}{2}}{2}\hspace {2cm}y_I=\frac {1+0}{2}

Pour calculer 1+\frac{7}{2} , il faut mettre au même dénominateur, ici 2.

x_I=\frac {{1}\times{\frac{2}{2}}+\frac{7}{2}}{2}\hspace {2cm}y_I=\frac {1}{2}

x_I=\frac {\frac{9}{2}}{2}\hspace {2cm}y_I=\frac {1}{2}

Pour calculer \frac {\frac{9}{2}}{2} , on utilise la propriété : diviser par 2 revient à multiplier par son inverse \frac {1}{2}.

x_I={\frac{9}{2}}\times{\frac{1}{2}}\hspace {2cm}y_I=\frac {1}{2}

x_I={\frac{9}{4}}\hspace {2cm}y_I=\frac {1}{2}

Donc I(\frac{9}{4};\frac {1}{2})

Tout d’abord, on ne cherche pas les coordonnées du milieu mais celles d’un des points. Ici le point D. Comme on ne connaît pas ses coordonnées, on les remplace par les lettres x et y.

On pose D(x;y)

On n’hésite pas à repérer les coordonnées des points D ,  I et B ainsi

\hspace{0.6cm} x_{D} y_{D} \hspace{0.6cm} x_{I} y_{I} \hspace{0.6cm} x_{B} y_{B}

\hspace{0.2cm} D(x;y) \hspace{0.4cm} I(\frac{9}{4};\frac{1}{2}) \hspace{0.4cm} B(5;3)  

On écrit la formule du cours :

x_I=\frac {x_D+x_B}{2}\hspace {2cm}y_I=\frac {y_D+y_B}{2}

Et on prend soin de bien remplacer les lettres par les bons nombres. Dans le cas d’un nombre négatif, on le met entre parenthèses.

\frac{9}{4}=\frac {x+5}{2}\hspace {2cm}\frac{1}{2}=\frac {y+3}{2}

Nous avons deux équations du premier degré à résoudre. La première \frac{9}{4}=\frac {x+5}{2} qu’on peut aussi écrire \frac {x+5}{2}=\frac{9}{4}.

Le 2 au dénominateur n’est pas à sa place, je multiplie par 2 de chaque côté de l’égalité.

x+5={\frac{9}{4}}\times{2}

Pour calculer {\frac{9}{4}}\times{2} plutôt que de multiplier entre les numérateurs et les dénominateurs, il vaut mieux d’abord simplifier d’abord par 2 en haut et en bas puis on multiplie ente numérateurs et dénominateurs.

x+5=\frac{9}{2}

Le 5 à gauche n’est pas à sa place, c’est un terme dans une somme. Le contraire d’ajouter 5 est enlever 5.

J’enlève 5 de chaque côté 

x=\frac{9}{2}-5

Pour calculer \frac{9}{2}-5 il faut mettre au même dénominateur, ici 2. On multiplie donc 5 en haut et en bas par 2.

x=\frac{9}{2}-{5}\times{\frac{2}{2}}

x=\frac{9-10}{2}

x=-\frac{1}{2}

La seconde \frac{1}{2}=\frac {y+3}{2} qu’on peut aussi écrire \frac {y+3}{2}=\frac{1}{2}.

Le 2 au dénominateur n’est pas à sa place. Le contraire de diviser par 2 est multiplier par 2.Je multiplie par 2 de chaque côté de l’égalité.

y+3={\frac{1}{2}}\times{2}

y+3=1

Le 3 à gauche n’est pas à sa place, c’est un terme dans une somme. Le contraire d’ajouter 3  est enlever 3.

J’enlève 3 de chaque côté 

y=1-3

y=-2

x+5=\frac{9}{2}\hspace {3cm} y+3=1

x=\frac{9}{2}-5 \hspace {3cm}y=1-3

x=\frac{9-10}{2}\hspace {3.5cm}y=-2

x=-\frac{1}{2}\hspace {3.5cm}y=-2

 

Donc C(-\frac{1}{2};-2)

Le quadrilatère ABCD est un parallélogramme car les diagonales ont le même milieu I.

On n’hésite pas à repérer les coordonnées des points A et B ainsi

\hspace{0.6cm} x_{A} y_{A} \hspace{0.6cm} x_{B} y_{B}

\hspace{0.2cm} A(1;1) \hspace{0.4cm} B(-3;-1)

On écrit la formule du cours :

AB=\sqrt {{(x_B-x_A) }^{2}+{(y_B-y_A) }^{2}} 

Et on prend soin de bien remplacer les lettres par les bons nombres. Dans le cas d’un nombre négatif, on le met entre parenthèses.

AB=\sqrt {{((-3)-1)}^{2}+{((-1)-1)}^{2}}

On calcule. On effectue d’abord ce qu’il y a entre parenthèses

AB=\sqrt {{(-4)}^{2}+{(-2)}^{2}} 

On effectue ensuite les puissances, ici les carrés. 

AB=\sqrt {16+4}

On effectue ensuite la somme

AB=\sqrt {20}

Pour finir, on regarde si on peut écrire 20 comme le produit d’un nombre de du carré d’un nombre. Ici 20={5}\times{{2}^{2}}

AB=\sqrt {{5}\times{{2}^{2}}}

On applique ensuite la règle suivante : \sqrt{a\times b}=\sqrt{a}\times\sqrt{b}

AB={\sqrt{5}}\times{\sqrt{{2}^{2}}}

Il ne reste plus qu’à appliquer la règle suivante : si a est positif ou nul alors \sqrt {{a}^{2}}=a

AB=2\sqrt {5}

On n’hésite pas à repérer les coordonnées des points A et B ainsi

\hspace{0.6cm} x_{A} y_{A} \hspace{0.6cm} x_{B} y_{B}

\hspace{0.2cm} A(-1;2) \hspace{0.4cm} B(-3;-4)

On écrit la formule du cours :

AB=\sqrt {{(x_B-x_A) }^{2}+{(y_B-y_A) }^{2}} 

Et on prend soin de bien remplacer les lettres par les bons nombres. Dans le cas d’un nombre négatif, on le met entre parenthèses.

AB=\sqrt {{((-3)-(-1))}^{2}+{((-4)-2)}^{2}}

On calcule. On effectue d’abord ce qu’il y a entre parenthèses

AB=\sqrt {{(-3+1)}^{2}+{(-4-2)}^{2}} 

AB=\sqrt {{(-2)}^{2}+{(-6)}^{2}} 

On effectue ensuite les puissances, ici les carrés. 

AB=\sqrt {4+36}

On effectue ensuite la somme

AB=\sqrt {40}

Pour finir, on regarde si on peut écrire 40 comme le produit d’un nombre de du carré d’un nombre. Ici 40={10}\times{{2}^{2}}

AB=\sqrt {{10}\times{{2}^{2}}}

On applique ensuite la règle suivante : \sqrt{a\times b}=\sqrt{a}\times\sqrt{b}

AB={\sqrt{10}}\times{\sqrt{{2}^{2}}}

Il ne reste plus qu’à appliquer la règle suivante : si a est positif ou nul alors \sqrt {{a}^{2}}=a

AB=2\sqrt {10}

On n’hésite pas à repérer les coordonnées des points A et B ainsi

\hspace{0.6cm} x_{A} y_{A} \hspace{0.6cm} x_{B} y_{B}

\hspace{0.2cm} A(1;\frac{2}{3}) \hspace{0.4cm} B(\frac{1}{5};-1)

On écrit la formule du cours :

AB=\sqrt {{(x_B-x_A) }^{2}+{(y_B-y_A) }^{2}} 

Et on prend soin de bien remplacer les lettres par les bons nombres. Dans le cas d’un nombre négatif, on le met entre parenthèses.

AB=\sqrt {{(\frac{1}{5}-1)}^{2}+{((-1)-\frac{2}{3})}^{2}} 

On calcule. On effectue d’abord ce qu’il y a entre parenthèses. Pour cela il faut mettre au même dénominateur.

AB=\sqrt {{(\frac{1}{5}-{1}\times\frac{5}{5})}^{2}+{({(-1)}\times\frac{3}{3}-\frac{2}{3})}^{2}}

AB=\sqrt {{(-\frac{4}{5})}^{2}+{(-\frac{5}{3})}^{2}}

On effectue ensuite les puissances, ici les carrés. 

AB=\sqrt {\frac{16}{25}+\frac{25}{9}}

On effectue ensuite la somme. Attention, il faut mettre au même dénominateur, ici 225.

AB=\sqrt {{\frac{16}{25}}\times{\frac{9}{9}}+{\frac{25}{9}}\times{\frac{25}{25}}}

AB=\sqrt {\frac{144+625}{225}} 

AB=\sqrt {\frac{769}{225}} 

On ne peut pas simplifier \frac{769}{225} 

AB=\frac{\sqrt {769}}{\sqrt{225}}

On ne peut pas écrire 769 comme le produit d’un nombre et du carré d’un nombre. En revanche 225 est le carré de 15.

AB=\frac{\sqrt {769}}{15}

 

Les coordonnées des points sont : A(0;3), B(4;0), C(0;-3) et D(-4;0)

On n’hésite pas à repérer les coordonnées des points A et B ainsi

\hspace{0.6cm} x_{A} y_{A} \hspace{0.6cm} x_{B} y_{B}

\hspace{0.2cm} A(0;3) \hspace{0.4cm} B(4;0)

On écrit la formule du cours :

AB=\sqrt {{(x_B-x_A) }^{2}+{(y_B-y_A) }^{2}} 

Et on prend soin de bien remplacer les lettres par les bons nombres. Dans le cas d’un nombre négatif, on le met entre parenthèses.

AB=\sqrt {{(4-0)}^{2}+{(0-3)}^{2}}

On calcule. On effectue d’abord ce qu’il y a entre parenthèses

AB=\sqrt {{(4)}^{2}+{(-3)}^{2}} 

On effectue ensuite les puissances, ici les carrés. 

AB=\sqrt {16+9}

On effectue ensuite la somme

AB=\sqrt {25}

AB=5

 

On n’hésite pas à repérer les coordonnées des points B et C ainsi

\hspace{0.6cm} x_{B} y_{B} \hspace{0.6cm} x_{C} y_{C}

\hspace{0.2cm}B(4;0) \hspace{0.4cm} C(0;-3)

On écrit la formule du cours :

BC=\sqrt {{(x_C-x_B) }^{2}+{(y_C-y_B) }^{2}} 

Et on prend soin de bien remplacer les lettres par les bons nombres. Dans le cas d’un nombre négatif, on le met entre parenthèses.

BC=\sqrt {{(0-4)}^{2}+{((-3)-0)}^{2}}

On calcule. On effectue d’abord ce qu’il y a entre parenthèses

BC=\sqrt {{(-4)}^{2}+{(-3)}^{2}} 

On effectue ensuite les puissances, ici les carrés. 

BC=\sqrt {16+9}

On effectue ensuite la somme

BC=\sqrt {25}

BC=5

 

On n’hésite pas à repérer les coordonnées des points C et D ainsi

\hspace{0.6cm} x_{C} y_{C} \hspace{0.6cm} x_{D} y_{D}

\hspace{0.2cm} C(0;-3) \hspace{0.4cm} D(-4;0)

On écrit la formule du cours :

DC=\sqrt {{(x_C-x_D) }^{2}+{(y_C-y_D) }^{2}} 

Et on prend soin de bien remplacer les lettres par les bons nombres. Dans le cas d’un nombre négatif, on le met entre parenthèses.

DC=\sqrt {{(0-(-4))}^{2}+{((-3)-0)}^{2}}

On calcule. On effectue d’abord ce qu’il y a entre parenthèses

DC=\sqrt {{(4)}^{2}+{(-3)}^{2}} 

On effectue ensuite les puissances, ici les carrés. 

CD=\sqrt {16+9}

On effectue ensuite la somme

CD=\sqrt {25}

 

CD=5

 

 

On n’hésite pas à repérer les coordonnées des points A et D ainsi

\hspace{0.6cm} x_{A} y_{A} \hspace{0.6cm} x_{D} y_{D}

\hspace{0.2cm} A(0;3) \hspace{0.4cm} D(-4;0)

On écrit la formule du cours :

DA=\sqrt {{(x_A-x_D) }^{2}+{(y_A-y_D) }^{2}} 

Et on prend soin de bien remplacer les lettres par les bons nombres. Dans le cas d’un nombre négatif, on le met entre parenthèses.

DA=\sqrt {{(0-(-4))}^{2}+{(3-0)}^{2}}

On calcule. On effectue d’abord ce qu’il y a entre parenthèses

AB=\sqrt {{(4)}^{2}+{(3)}^{2}} 

On effectue ensuite les puissances, ici les carrés. 

AB=\sqrt {16+9}

On effectue ensuite la somme

AB=\sqrt {25}

AB=5

 

ABCD est losange car il possède quatre côtés de même longueur.

2.coordonnéescoursfin

On n’hésite pas à repérer les coordonnées des points A et B ainsi

\hspace{0.6cm} x_{A} y_{A} \hspace{0.6cm} x_{B} y_{B}

\hspace{0.2cm} A(-2;0) \hspace{0.4cm} B(1;3)

On écrit la formule du cours :

AB=\sqrt {{(x_B-x_A) }^{2}+{(y_B-y_A) }^{2}} 

Et on prend soin de bien remplacer les lettres par les bons nombres. Dans le cas d’un nombre négatif, on le met entre parenthèses.

AB=\sqrt {{(1-(-2))}^{2}+{(3-0)}^{2}}

On calcule. On effectue d’abord ce qu’il y a entre parenthèses

AB=\sqrt {{3}^{2}+{3}^{2}} 

On effectue ensuite les puissances, ici les carrés. 

AB=\sqrt {9+9}

On effectue ensuite la somme

AB=\sqrt {18}

Pour finir, on regarde si on peut écrire 18 comme le produit d’un nombre de du carré d’un nombre. Ici 18={2}\times{{3}^{2}}

AB=\sqrt {{2}\times{{3}^{2}}}

On applique ensuite la règle suivante : \sqrt{a\times b}=\sqrt{a}\times\sqrt{b}

AB={\sqrt{2}}\times{\sqrt{{3}^{2}}}

Il ne reste plus qu’à appliquer la règle suivante : si a est positif ou nul alors \sqrt {{a}^{2}}=a

AB=3\sqrt {2}

On n’hésite pas à repérer les coordonnées des points B et C ainsi

\hspace{0.6cm} x_{B} y_{B} \hspace{0.6cm} x_{C} y_{C}

\hspace{0.2cm} B(1;3) \hspace{0.4cm} C(4;2)

On écrit la formule du cours :

BC=\sqrt {{(x_C-x_B) }^{2}+{(y_C-y_B) }^{2}} 

Et on prend soin de bien remplacer les lettres par les bons nombres. Dans le cas d’un nombre négatif, on le met entre parenthèses.

BC=\sqrt {{(4-1)}^{2}+{(2-3)}^{2}}

On calcule. On effectue d’abord ce qu’il y a entre parenthèses

BC=\sqrt {{3}^{2}+{(-1)}^{2}} 

On effectue ensuite les puissances, ici les carrés. 

BC=\sqrt {9+1}

On effectue ensuite la somme

BC=\sqrt {10}

 

On n’hésite pas à repérer les coordonnées des points C et D ainsi

\hspace{0.6cm} x_{C} y_{C} \hspace{0.6cm} x_{D} y_{D}

\hspace{0.2cm} C(4;2) \hspace{0.4cm} D(1;-1)

On écrit la formule du cours :

CD=\sqrt {{(x_D-x_C) }^{2}+{(y_D-y_C) }^{2}} 

Et on prend soin de bien remplacer les lettres par les bons nombres. Dans le cas d’un nombre négatif, on le met entre parenthèses.

CD=\sqrt {{(1-4)}^{2}+{((-1)-2)}^{2}}

On calcule. On effectue d’abord ce qu’il y a entre parenthèses

CD=\sqrt {{(-3)}^{2}+{(-3)}^{2}} 

On effectue ensuite les puissances, ici les carrés. 

CD=\sqrt {9+9}

On effectue ensuite la somme

CD=\sqrt {18}

Pour finir, on regarde si on peut écrire 18 comme le produit d’un nombre du carré d’un nombre. Ici 18={2}\times{{3}^{2}}

CD=\sqrt {{2}\times{{3}^{2}}}

On applique ensuite la règle suivante : \sqrt{a\times b}=\sqrt{a}\times\sqrt{b}

CD={\sqrt{2}}\times{\sqrt{{3}^{2}}}

Il ne reste plus qu’à appliquer la règle suivante : si a est positif ou nul alors \sqrt {{a}^{2}}=a

CD=2\sqrt {3}

On n’hésite pas à repérer les coordonnées des points D et A ainsi

\hspace{0.6cm} x_{D} y_{D} \hspace{0.6cm} x_{A} y_{A}

\hspace{0.2cm} D(1;-1) \hspace{0.4cm} A(-2;0)

On écrit la formule du cours :

DA=\sqrt {{(x_A-x_D) }^{2}+{(y_A-y_D) }^{2}} 

Et on prend soin de bien remplacer les lettres par les bons nombres. Dans le cas d’un nombre négatif, on le met entre parenthèses.

DA=\sqrt {{((-2)-1)}^{2}+{(0-(-1))}^{2}}

On calcule. On effectue d’abord ce qu’il y a entre parenthèses

DA=\sqrt {{(-3)}^{2}+{1}^{2}} 

On effectue ensuite les puissances, ici les carrés. 

DA=\sqrt {9+1}

On effectue ensuite la somme

AB=\sqrt {10}

 

 

Le quadrilatère ABCD est un parallélogramme car ses côtés opposés ont même longueur.

On n’hésite pas à repérer les coordonnées des points A et B ainsi

\hspace{0.6cm} x_{A} y_{A} \hspace{0.6cm} x_{B} y_{B}

\hspace{0.2cm} A(-2;5) \hspace{0.4cm} B(1;3)

On écrit la formule du cours :

x_I=\frac {x_A+x_B}{2}\hspace {2cm}y_I=\frac {y_A+y_B}{2}

Et on prend soin de bien remplacer les lettres par les bons nombres. Dans le cas d’un nombre négatif, on le met entre parenthèses.

x_I=\frac {(-2)+1}{2}\hspace {2cm}y_I=\frac {5+3}{2}

On calcule. Si vous utilisez la calculatrice , tapez cette séquence de calcul (-2+1))/2 en utilisant les parenthèses « invisibles  » qui entourent le numérateur. Si vous tapez -2+1/2, vous obtiendrez -1.5 car la machine calculera 1/2 en priorité ce qui est faux

x_I=-\frac {1}{2}\hspace {2cm}y_I=\frac {8}{2}

x_I=-\frac {1}{2}\hspace {2cm}y_I=4

Donc I(-\frac {1}{2};4)

On calcule d’abord la longueur du diamètre [AB ]

On n’hésite pas à repérer les coordonnées des points A et B ainsi

\hspace{0.6cm} x_{A} y_{A} \hspace{0.6cm} x_{B} y_{B}

\hspace{0.2cm} A(-2;5) \hspace{0.4cm} B(1;3)

On écrit la formule du cours :

AB=\sqrt {{(x_B-x_A) }^{2}+{(y_B-y_A) }^{2}} 

Et on prend soin de bien remplacer les lettres par les bons nombres. Dans le cas d’un nombre négatif, on le met entre parenthèses.

AB=\sqrt {{(1-(-2))}^{2}+{(3-5)}^{2}}

On calcule. On effectue d’abord ce qu’il y a entre parenthèses

AB=\sqrt {{3}^{2}+{(-2)}^{2}} 

On effectue ensuite les puissances, ici les carrés. 

AB=\sqrt {9+4}

On effectue ensuite la somme

AB=\sqrt {13}

Pour déterminer le rayon, on divise la longueur du diamètre par 2, donc

R= \frac{\sqrt {13}}{2}

 

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.