SOMMAIRE
Déterminer graphiquement l’image d’un nombre a.
METHODE
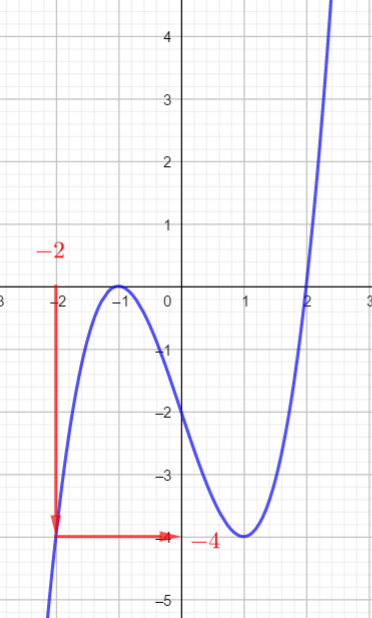
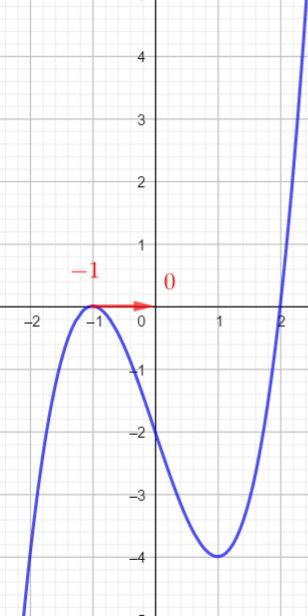
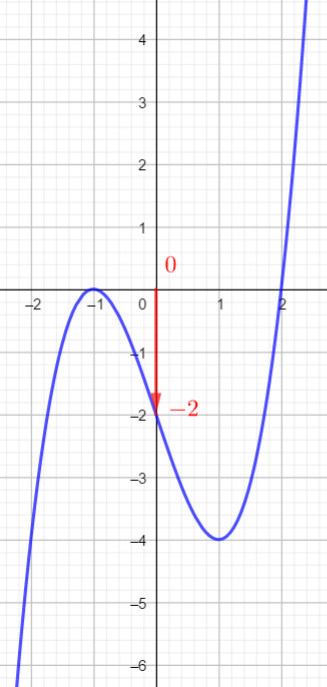
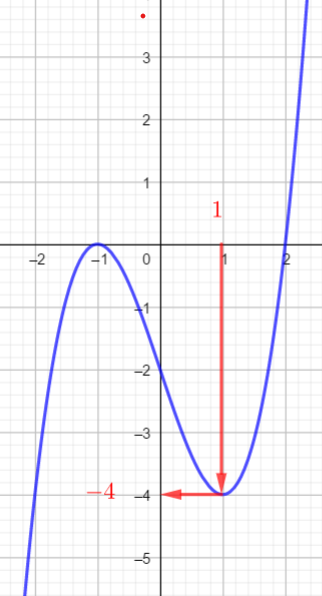
- Je place a sur l’axe des abscisses.
- Je trace la droite parallèle à l’axe des ordonnées passant par a jusqu’à la courbe
- A partir du point de la courbe trouvé, je trace la droite parallèle à l’axe des abscisses jusqu’à l’axe des ordonnées et je lis alors l’image de a.
- Pour valider ma réponse, je peux vérifier que le point qui a pour coordonnées : a et l’image de a est situé sur la courbe.
EXERCICE N°1
En utilisant la courbe ci-dessous, déterminer les images de -2; -1; 0; 1 ;2
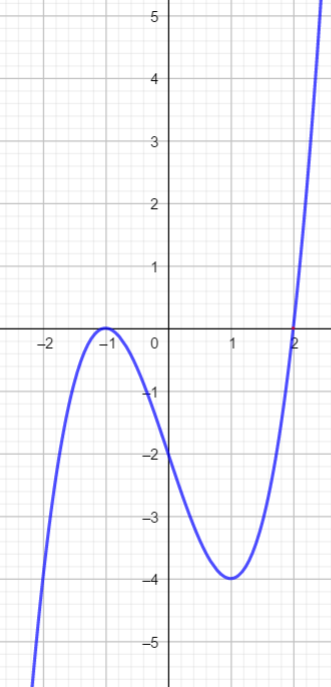
Déterminer graphiquement le ou les antécédents s’il(s) existe(nt) d’un nombre réel b ou résoudre graphiquement f(x) = b .
METHODE
- Je place b sur l’axe des ordonnées
- Je trace la parallèle à l’axe des abscisses passant par b toute entière , d’un bord à l’autre du repère
- Je repère les points d’intersection éventuels de la droite et de la courbe
- Je lis les abscisses de ces points d’intersections qui sont les antécédents de b
EXERCICE N°2
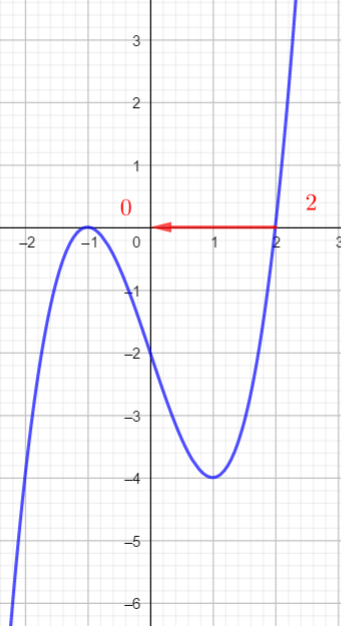
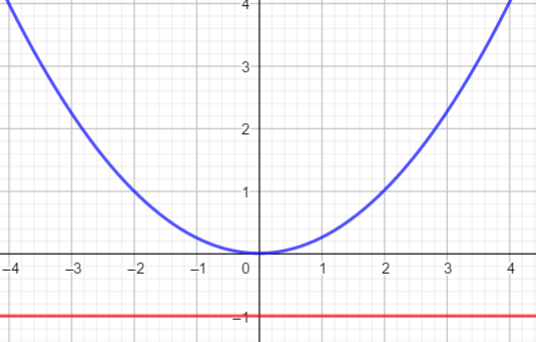
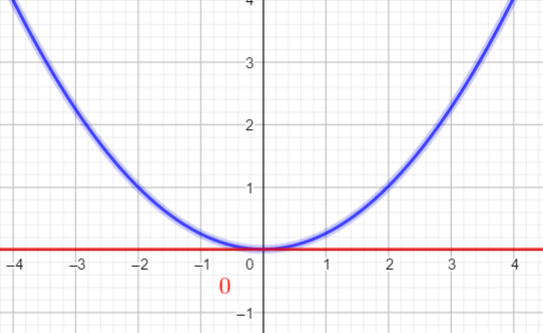
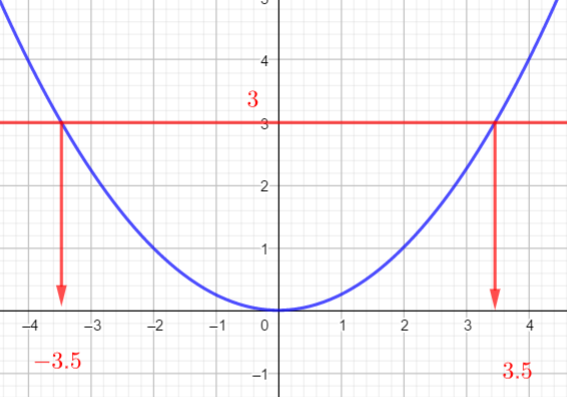
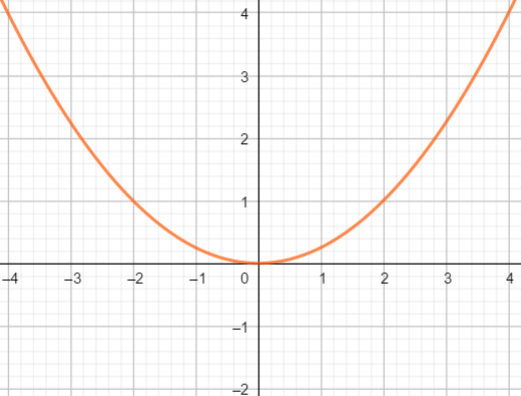
En utilisant la courbe ci-dessous
- déterminer les antécédents éventuels de -1; 0 ; 3
- Résoudre graphiquement f(x)=1
Pour faire le tableau de variations par lecture graphique .
METHODE
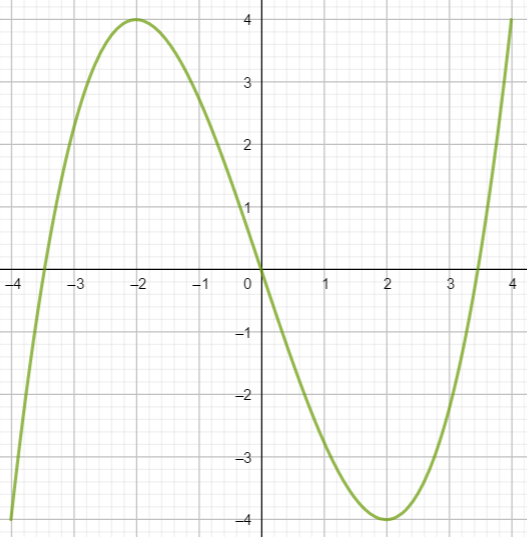
Les abscisses des points de la courbe varient entre -4 et 4
Si je mets mon index sur l’extrémité gauche de la courbe et que je parcours la courbe de gauche à droite, mon index monte puis descend puis monte comme la courbe.
Mon doigt arrête de monter pour redescendre pour la valeur -2 sur l’axe des abscisses ; puis mon doigt arrête de descendre pour remonter pour la valeur 2 sur l’axe des abscisses. .
L’image de -4 est à peu près -4, l’image de -2est 4 , l’image de 2 est -4 et l’image de 4 est 4
Voici donc le tableau de variation :
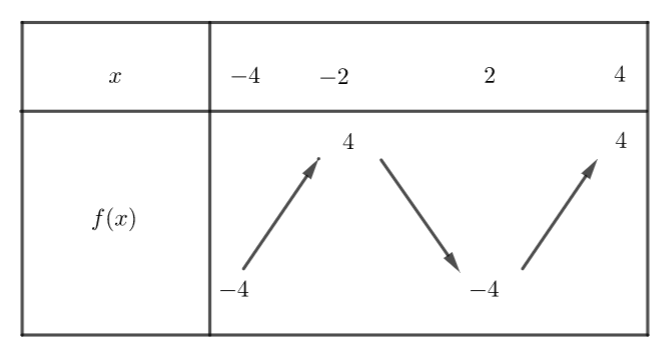
EXERCICE N°3
En utilisant la courbe ci-dessous, dresser le tableau de variation.
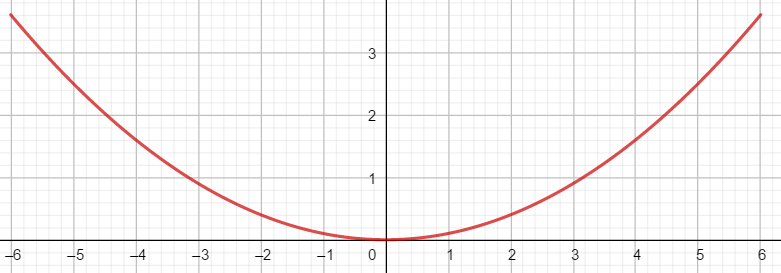
Pour déterminer s’il existe un minimum ou un maximum.
METHODE
Lorsqu’il y a sur la courbe un point de coordonnées (a;b) situé plus bas que tous les autres, on dit qu’il y a un minimum, sa valeur est b et ce minimum est atteint pour x=a
Lorsqu’il y a sur la courbe un point de coordonnées (a;b) situé plus haut que tous les autres, on dit qu’il y a un maximum, sa valeur est b et ce maximum est atteint pour x=a
EXERCICE N°4
Déterminer graphiquement les minimum et maximum à l’aide de la courbe ci-dessous.
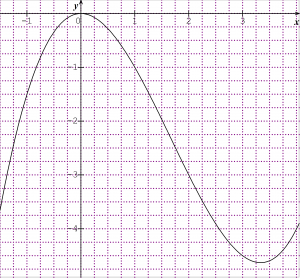
Pour tracer une droite d’équation y=ax+b
METHODE
Je place b l’ordonnée à l’origine sur l’axe des ordonnées.
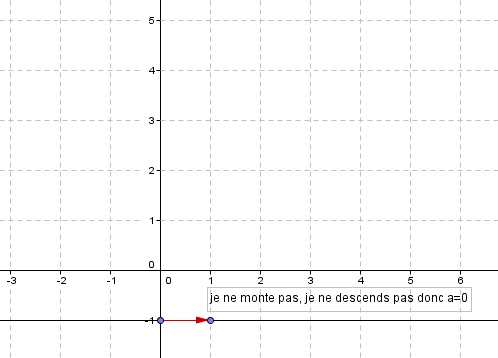
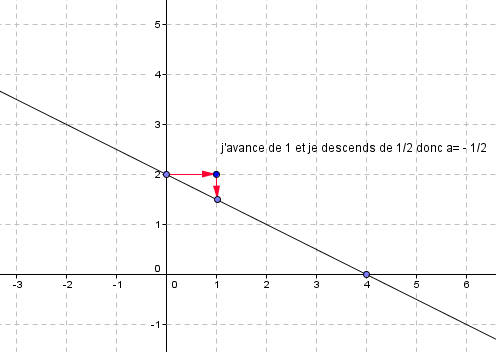
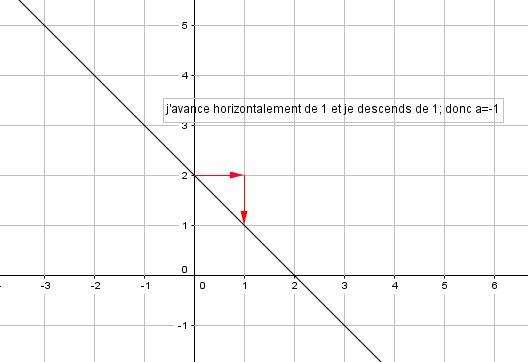
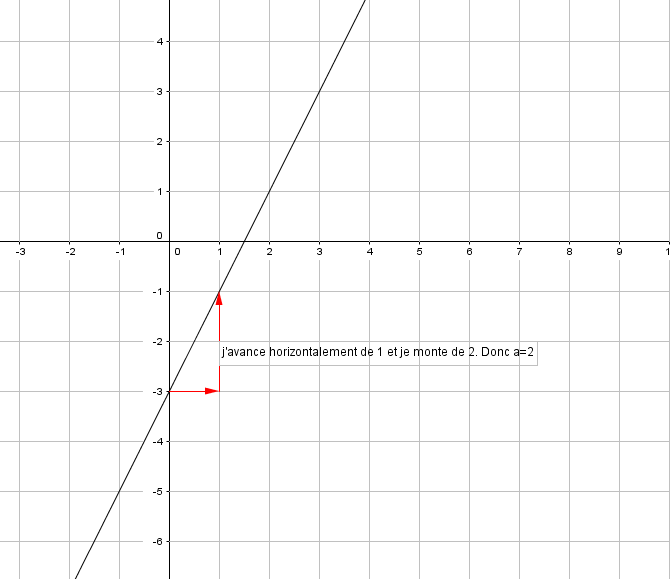
A partir de ce point, j’avance toujours d’une graduation et je me déplace verticalement pour retomber sur la droite : je monte de a si le coefficient directeur est positif et je descends de a si le coefficient directeur est négatif.
EXERCICE N°5
Déterminer, si c’est possible, les équations réduites des quatre droites ci-dessous.
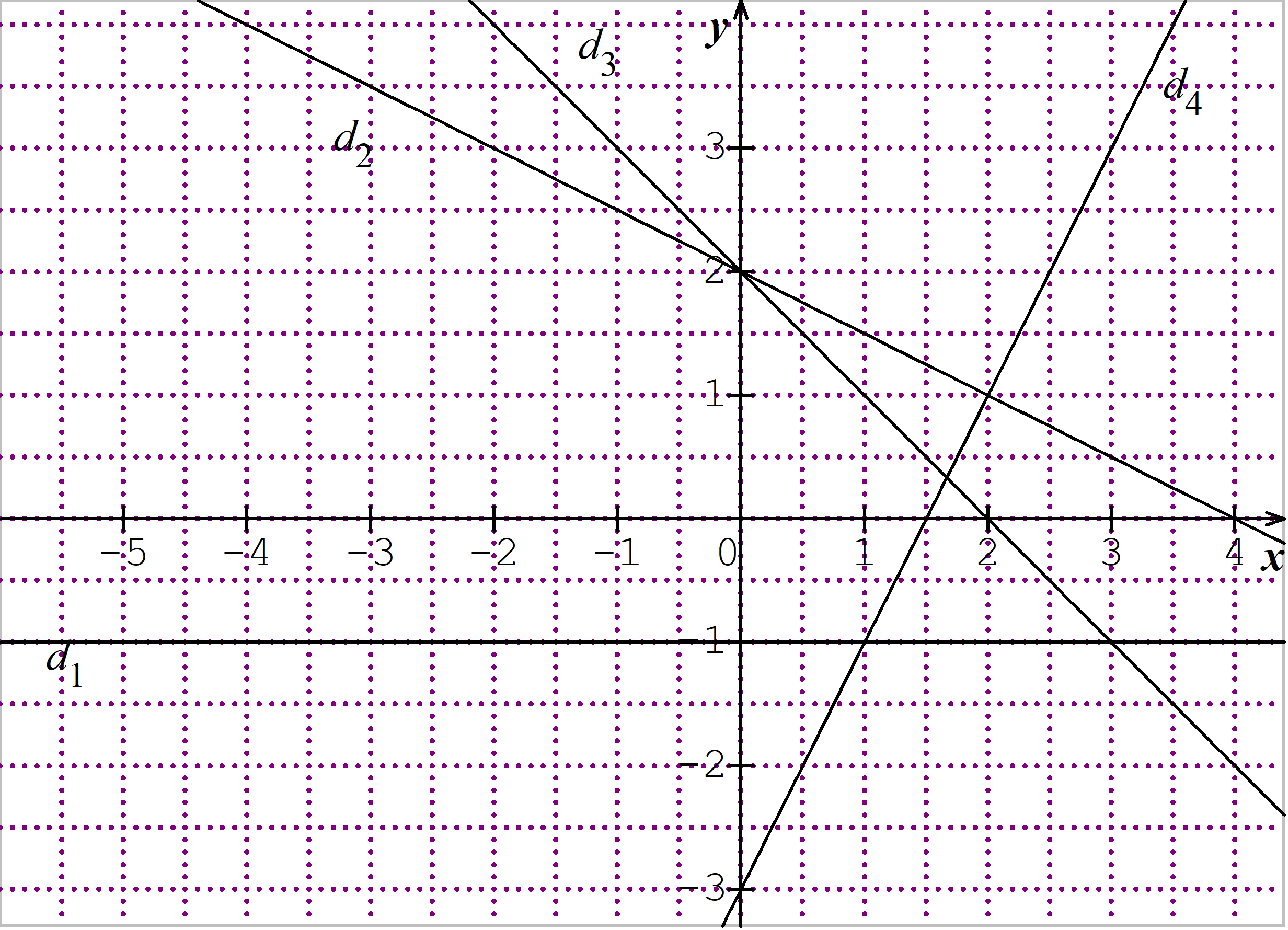
Résoudre graphiquement des inéquations du type f(x) inférieur à a
METHODE :
1) je place a sur l’axe des ordonnées et je trace la droite d’équation y=a
2) je traduis l’inégalité en langue française. Je remplace f(x) par « la courbe », < par « en-dessous et pas sur », > par au-dessus et pas sur », \leq par « en-dessous ou sur » et \geq par « au-dessus ou sur » et a par « la droite d’équation y=a ».
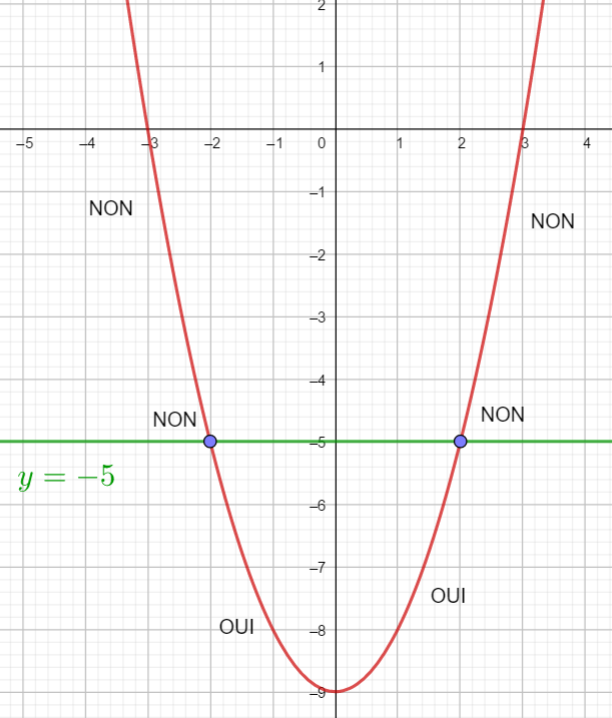
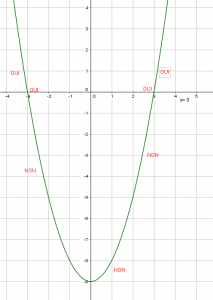
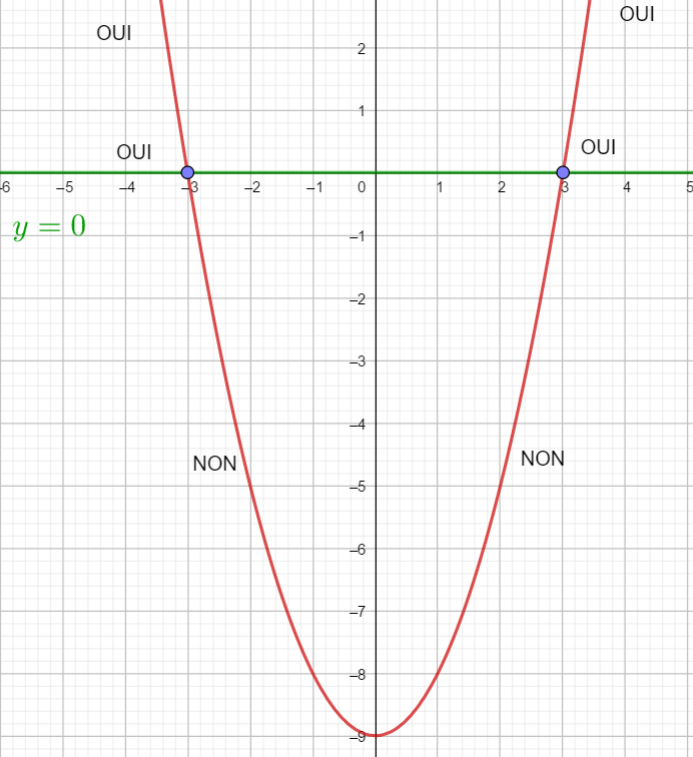
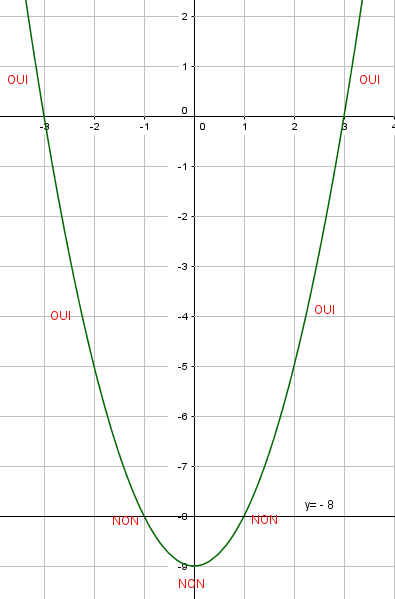
3) Je place mon index sur l’extrémité gauche de la courbe et je parcours la courbe de la gauche vers la droite en disant oui quand la courbe est bien placée par rapport à la droite (voir la phrase en français du paragraphe 2) et en disant non dans le cas contraire.
4) J’identifie sur l’axe des abscisses les valeurs de x pour lesquelles j’ai dit oui et j’écris cet ensemble sous forme d’intervalles ou de réunion d’intervalles.
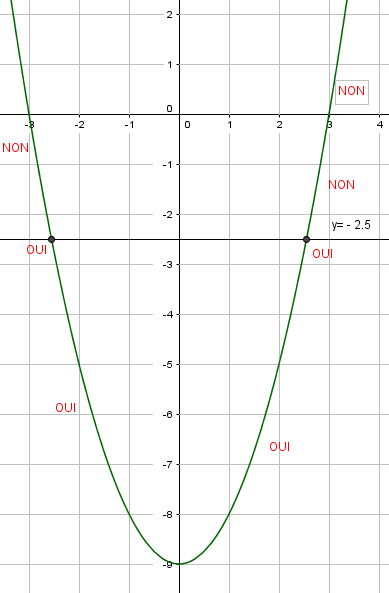
EXERCICE N°6
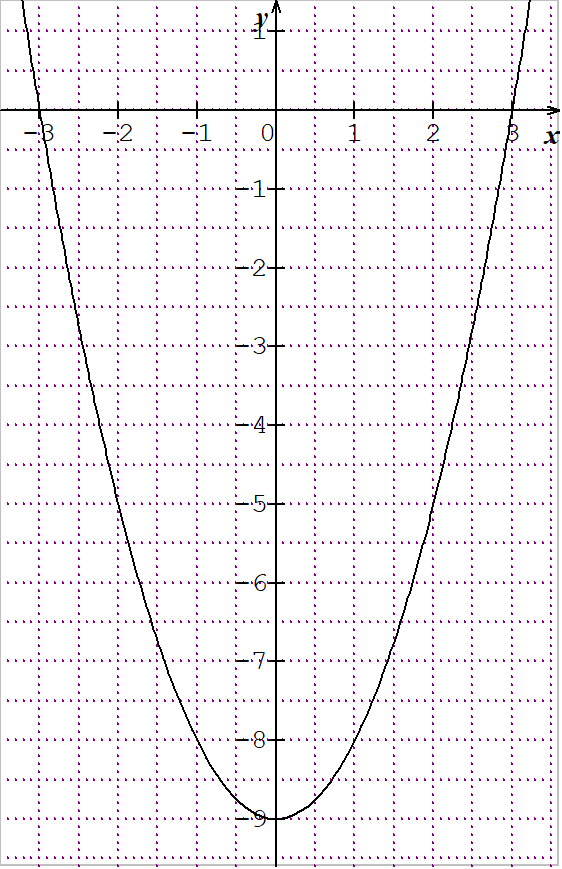
Résoudre les inéquations suivantes : f(x)<-5 ; f(x)\geq 0;f(x)>-8 et f(x)\leq-2.5 .
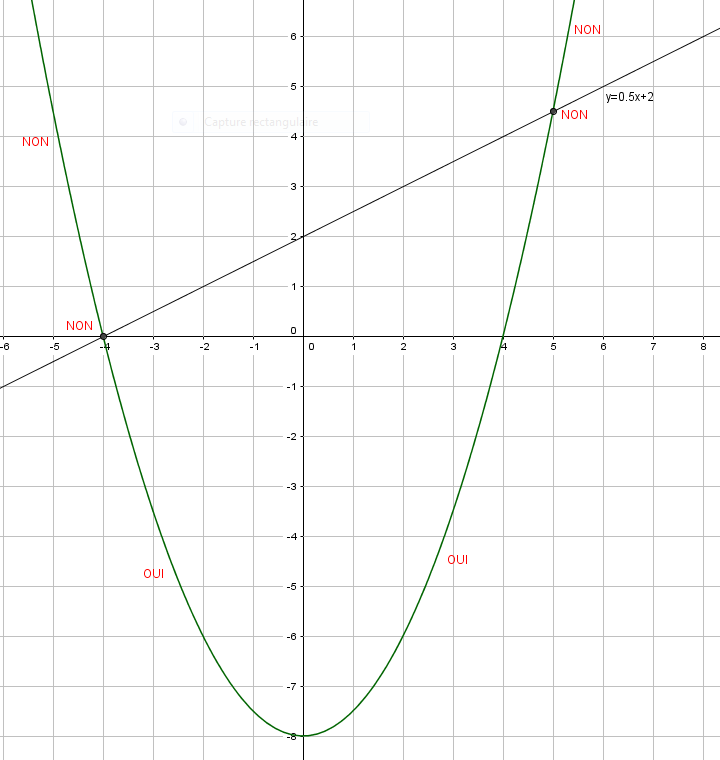
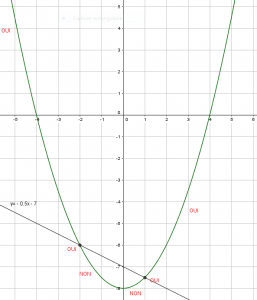
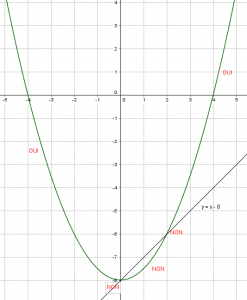
EXERCICE N°7
Résoudre graphiquement f(x)<0.5x+2 ; f(x)\geq-0.5x-7 ; f(x)>x-8
Vous pouvez utiliser la fenêtre Géogébra au-dessus pour tracer les droites. Il suffit de saisir, par exemple, y=0.5x+2 dans la colonne Algèbre située à gauche.