2.Résoudre une inéquation du premier degré

Niveau seconde, Nombres et calculs, Résoudre une inéquation du premier degré

Exemples de résolution d’inéquations du premier degré à une inconnue

exemple n°1

résoudre dans $R$ , l’inéquation $5x-2<3$

Pour résoudre l’inéquation du premier degré à une inconnue suivante

5x-2<3

Il faut remettre à leur place les membres qui ne sont pas à leur place en sachant que la résolution sera finie lorsqu’il ne restera que $x$ à gauche.

$-2$ n’est pas à sa place, j’ajoute $2$ de chaque côté. Le sens de l’inégalité ne change pas.

5x<3+2\\5x<5

$5$ n’est pas à sa place, je divise par $5$ de chaque côté. Le sens de l’inégalité ne change pas car on divise par un nombre positif.

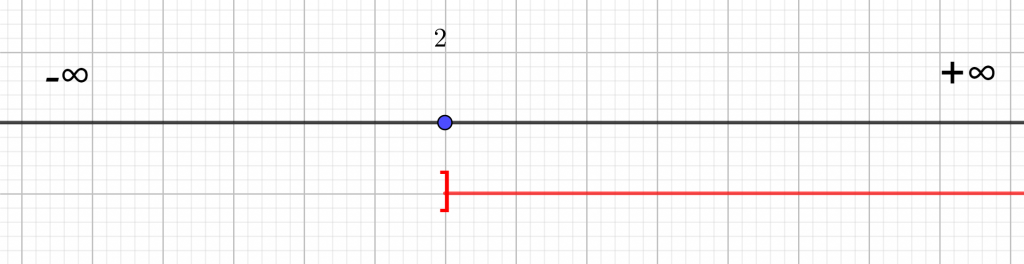
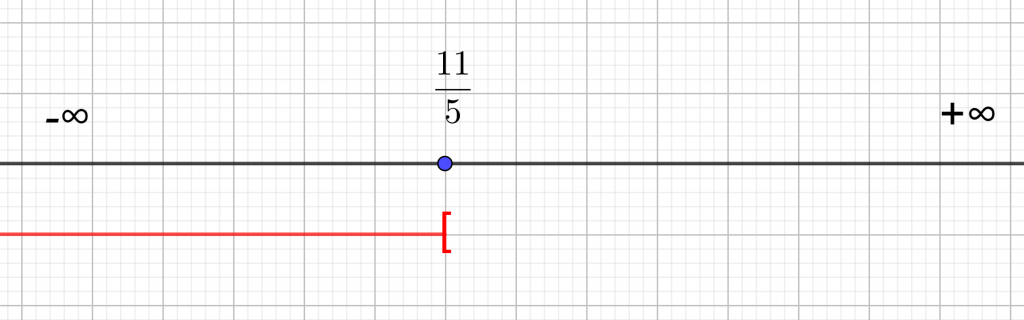
x<\frac{5}{5}\\x<1

Je matérialise l’ensemble-solution à l’aide de la droite réelle. Comme les solutions sont plus petites que $1$ je trace la demi-droite rouge située à gauche de $1$ . Comme $x<1$ , cela signifie que $x$ ne peut pas être égal à $1$ . Pour exclure la valeur $1$ de l’ensemble – solution, il faut que le crochet de l’intervalle soit ouvert c’est-à-dire que le crochet soit tourné vers l’extérieur. Du côté de l’infini, le crochet est toujours ouvert, c’est-à-dire tourné vers l’extérieur.

$S=]-\infty:1[$

exemple n°2

résoudre dans $R$ , l’inéquation $-3x+1\leq6$

Pour résoudre l’inéquation du premier degré à une inconnue suivante

-3x+1\leq6

Il faut remettre à leur place les membres qui ne sont pas à leur place en sachant que la résolution sera finie lorsqu’il ne restera que $x$ à gauche.

$1$ n’est pas à sa place, j’enlève 1 de chaque côté. Le sens de l’inégalité ne change pas.

-3x\leq6-1\\-3x\leq5

$-3$ n’est pas à sa place, je divise par $-3$ de chaque côté. Le sens de l’inégalité change car on divise par un nombre négatif.

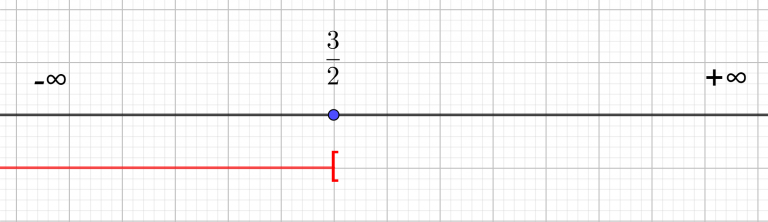
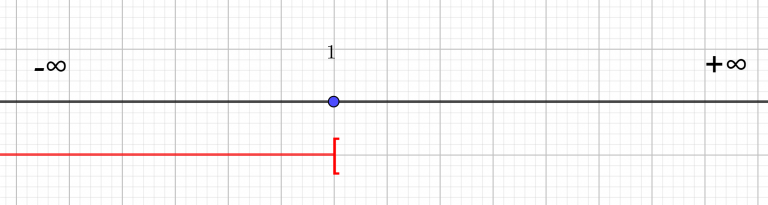
x\geq-\frac{5}{3}

Je matérialise l’ensemble-solution à l’aide de la droite réelle. Comme les solutions sont plus grandes que $-\frac{5}{3}$ je trace la demi-droite rouge située à droite de $-\frac{5}{3}$ . Comme $x\geq-\frac{5}{3}$ , cela signifie que $x$ peut être égal à $-\frac{5}{3}$ . Pour enfermer la valeur $-\frac{5}{3}$ dans l’ensemble – solution, il faut que le crochet de l’intervalle soit fermé c’est-à-dire que le crochet soit tourné vers l’intérieur de l’intervalle. Du côté de l’infini, le crochet est toujours ouvert, c’est-à-dire tourné vers l’extérieur de l’intervalle.

$S=[-\frac{5}{3};+\infty[$

exemple n°3

résoudre dans

R

, l’inéquation

2x+1\geq4x+4

Pour résoudre l’inéquation du premier degré à une inconnue suivante

2x+1\geq4x+4

Il faut remettre à leur place les membres qui ne sont pas à leur place en sachant que la résolution sera finie lorsqu’il ne restera que $x$ à gauche.

$1$ n’est pas à sa place, j’enlève 1 de chaque côté. Le sens de l’inégalité ne change pas.

2x\geq4x+4-1\\2x\geq4x+3

$4x$ n’est pas à sa place, j’enlève $4x$ de chaque côté. Le sens de l’inégalité ne change pas.

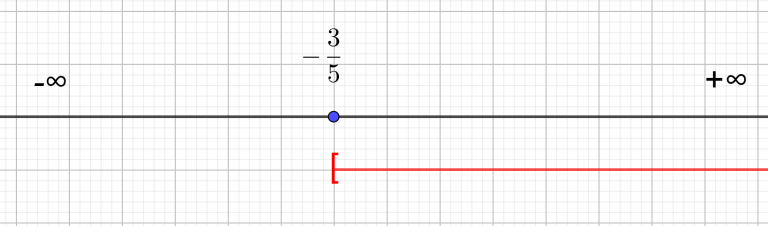
2x-4x\geq3\\-2x\geq3

$-2$ n’est pas à sa place, je divise par $-2$ de chaque côté. Le sens de l’inégalité change car on divise par un nombre négatif.

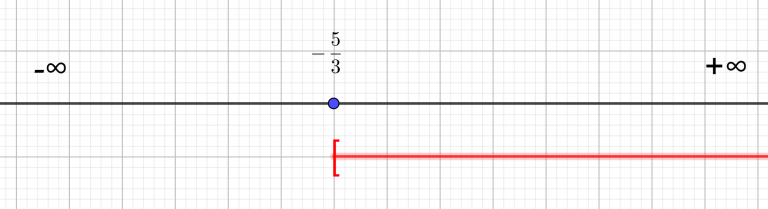
x\leq-\frac{3}{2}

Je matérialise l’ensemble-solution à l’aide de la droite réelle. Comme les solutions sont plus petites que $-\frac{3}{2}$ je trace la demi-droite rouge située à gauche de $-\frac{3}{2}$ . Comme $x\leq-\frac{3}{2}$ , cela signifie que $x$ peut-être égal à $-\frac{3}{2}$ . Pour enfermer la valeur $-\frac{3}{2}$ dans l’ensemble -solution, j’utilise un crochet fermé ( il est tourné vers l’intérieur de l’intervalle.)

S=]-\infty;-\frac{3}{2}]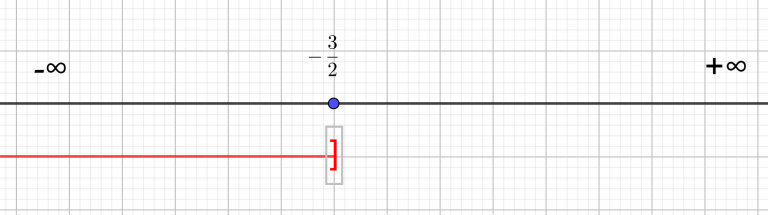

exemple n°4

résoudre dans $R$ , l’inéquation $4(2x-1)>2$

Pour résoudre l’inéquation du premier degré à une inconnue suivante

4(2x-1)>2

Ici, il faut d’abord développer $4(2x-1)$ avant tout.

8x-4>2

Il faut remettre à leur place les membres qui ne sont pas à leur place en sachant que la résolution sera finie lorsqu’il ne restera que $x$ à gauche.

$-4$ n’est pas à sa place, j’ajoute $4$ de chaque côté. Le sens de l’inégalité ne change pas.

$8x>2+4$

$8x>6$

$8$ n’est pas à sa place, je divise par $8$ de chaque côté. Le sens de l’inégalité ne change pas car on divise par un nombre positif.

x>\frac{6}{8}

Je peux mettre la fraction $\frac{6}{8}$ sous forme irréductible en simplifiant en haut et en bas par $2$

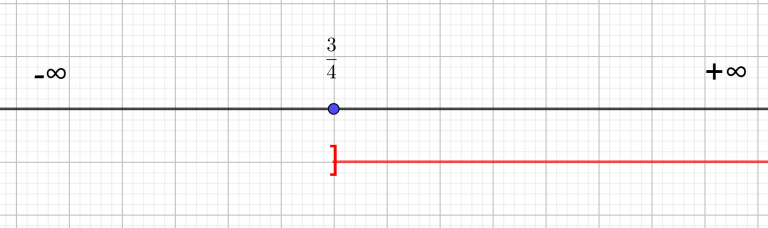
x>\frac{3}{4}

Je matérialise l’ensemble-solution à l’aide de la droite réelle. Comme les solutions sont plus grandes que $\frac{3}{4}$ je trace la demi-droite rouge située à droite de $\frac{3}{4}$ . Comme $x>\frac{3}{4}$ , cela signifie que $x$ ne peut pas être égal à $\frac{3}{4}$ . Pour exclure $\frac{3}{4}$ de l’ensemble – solution, il faut que le crochet de l’intervalle soit ouvert c’est-à-dire que le crochet soit tourné vers l’extérieur. Du côté de l’infini, le crochet est toujours ouvert, c’est-à-dire tourné vers l’extérieur.

$S=]\frac{3}{4};+\infty[$

Exercice

dans chaque cas, résoudre dans $R$ , les inéquations suivantes.

a) résoudre dans $R$ , l’inéquation $3x-4>2$

b) résoudre dans $R$ , l’inéquation $-4x+2\leq 6$

c) résoudre dans $R$ , l’inéquation $5x-5\geq -8$

d) résoudre dans $R$ , l’inéquation $-6x+1>-2-4x$

e) résoudre dans $R$ , l’inéquation $7(x-3)<2(x-5)$

Après avoir répondu aux différentes questions, valider les réponses avec la fenêtre Géogébra ci-dessous. Pour ce faire saisir par exemple $3x-4>2$ sur la ligne 1 puis cliquer sur le septième onglet en haut en partant de la gauche. Sur la ligne suivante apparaît Résoudre $\{x>2\}$ .

Pour saisir $\geq$ taper sur > puis sur =