logo

2.Variations des fonctions de référence.

Sommaire

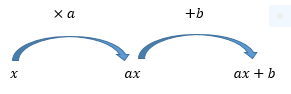
Fonctions affines

Variations

Exemple n°1 : \textbf{a>0}

  f(x)=0.5x+2

représentation graphique

2. variations affine+ courbe

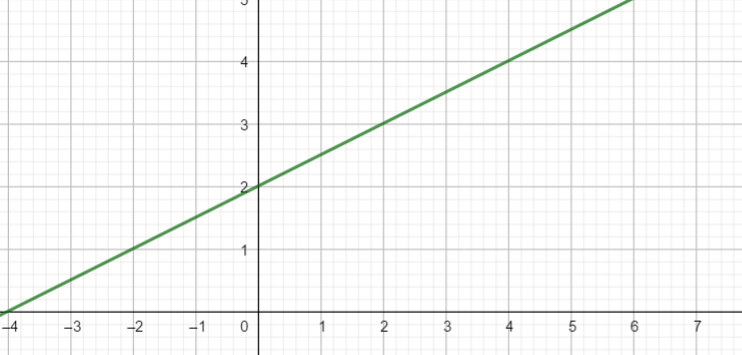
Sur l’intervalle  [-4;6], la courbe monte.

représentation tableur

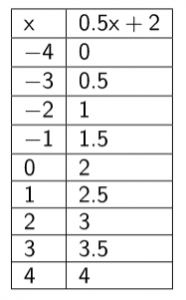
Il semble que les nombres et leurs images varient dans le même sens.

représentation algébrique

f(x)=0.5x+2 définie sur  \mathbb{R}  

Lorsque a est positif, la fonction affine définie sur \mathbb{R}  par  f(x)=ax+b  est croissante. 

si x_{1}< x_{2}

alors ax_{1}+b<ax_{2}+b

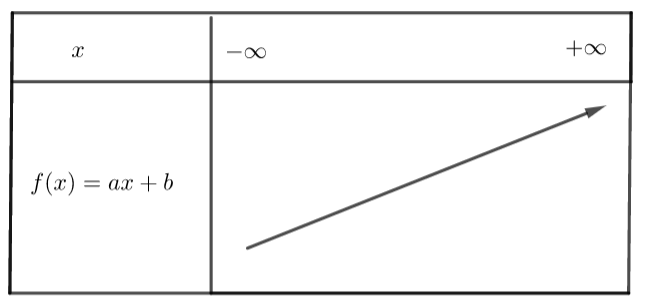
Voici le tableau de variation de la fonction affine définie sur \mathbb{R}  par  f(x)=ax+b lorsque a est positif.

Méthodes pour démontrer que f est croissante.
démonstration méthode n°1
démonstration méthode n°2

Exemple n°2 : \textbf{a<0}

  f(x)=-2x+4

représentation graphique

2. variations affine- courbe

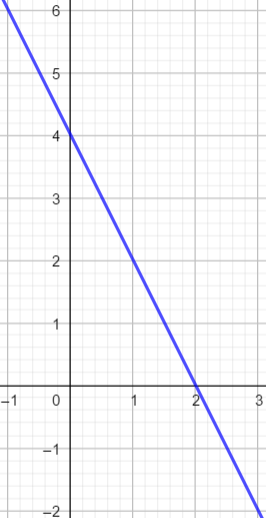
Sur l’intervalle  [-1;3], la courbe descend.

représentation tableur

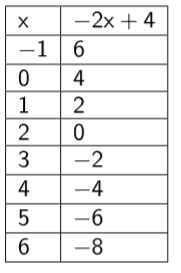
Il semble que les nombres et leurs images varient en sens contraire.

représentation algébrique

f(x)=-2x+4 définie sur \mathbb{R}  

Lorsque a est négatif, la fonction affine définie sur \mathbb{R}  par  f(x)=ax+b  est décroissante. 

si x_{1}<x_{2}

alors ax_{1}+b> ax_{2}+b

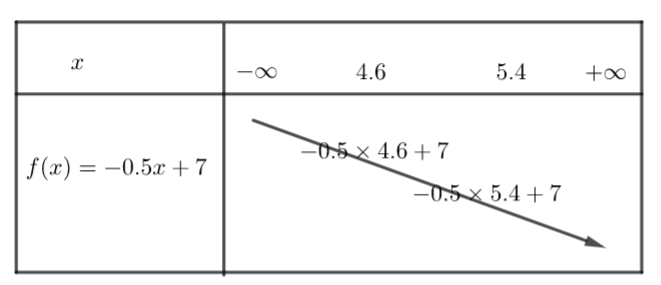
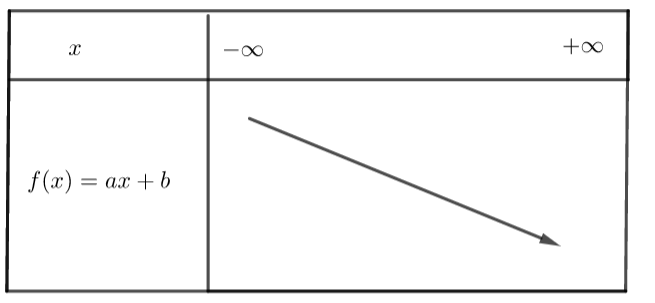
Voici le tableau de variation de la fonction affine définie sur \mathbb{R}  par  f(x)=ax+b lorsque a est négatif.

Méthodes pour démontrer que f est décroissante.
démonstration méthode n°1
démonstration méthode n°2

Exercice n°1

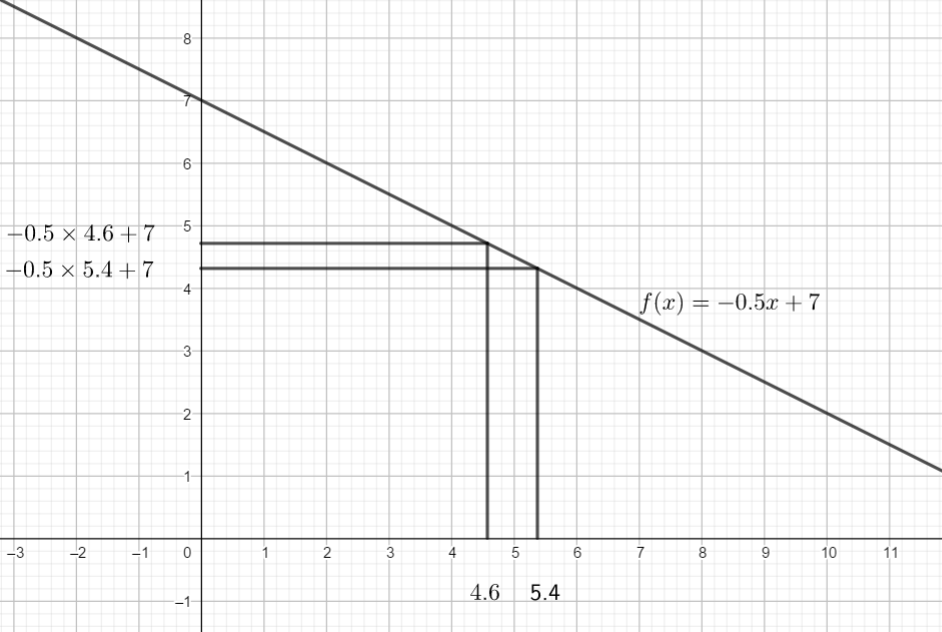
 Sans calcul, comparer les réels suivants

a) {-0.5}\times{5.4}+7 et {-0.5}\times{4.6}+7 

conjecture avec la courbe d'une fonction
conjecture avec le tableau de variations d'une fonction
correction avec les variations d'une fonction

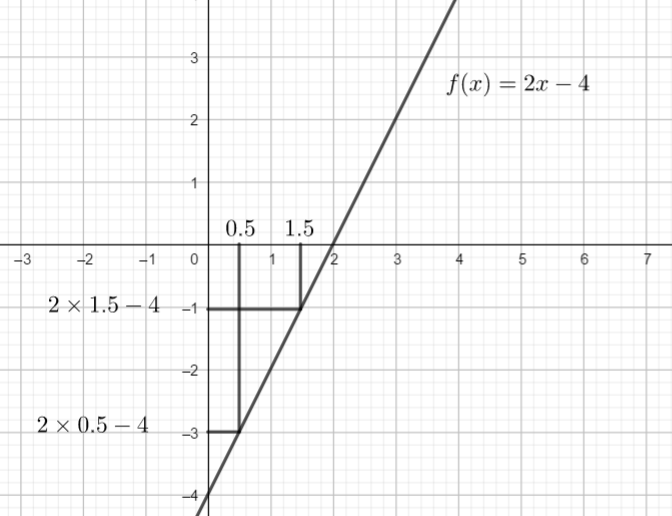
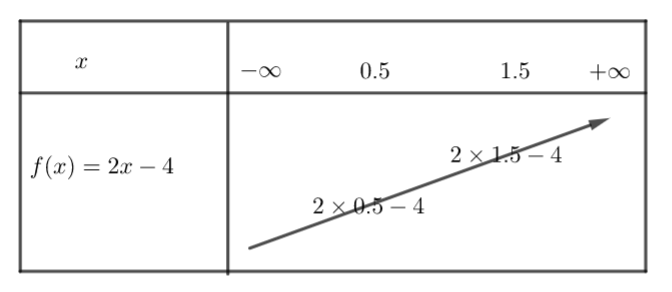
b) {2}\times{0.5}-4 et {2}\times{1.5}-4 

conjecture avec la courbe d'une fonction
conjecture avec le tableau de variations d'une fonction
correction avec les variations d'une fonction

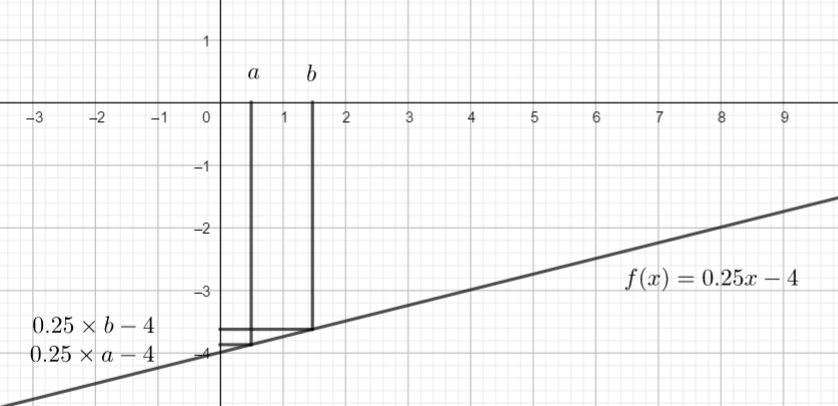
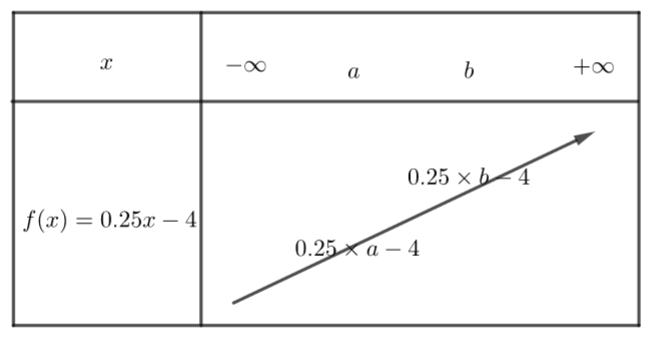
c) {0.25}\times{a}-4 et {0.25}\times{b}-4 en sachant que a<b.

conjecture avec la courbe d'une fonction
conjecture avec le tableau de variations d'une fonction
correction avec les variations d'une fonction

la fonction carré

variations

représentation graphique

2. représentation algébrique(1)1b

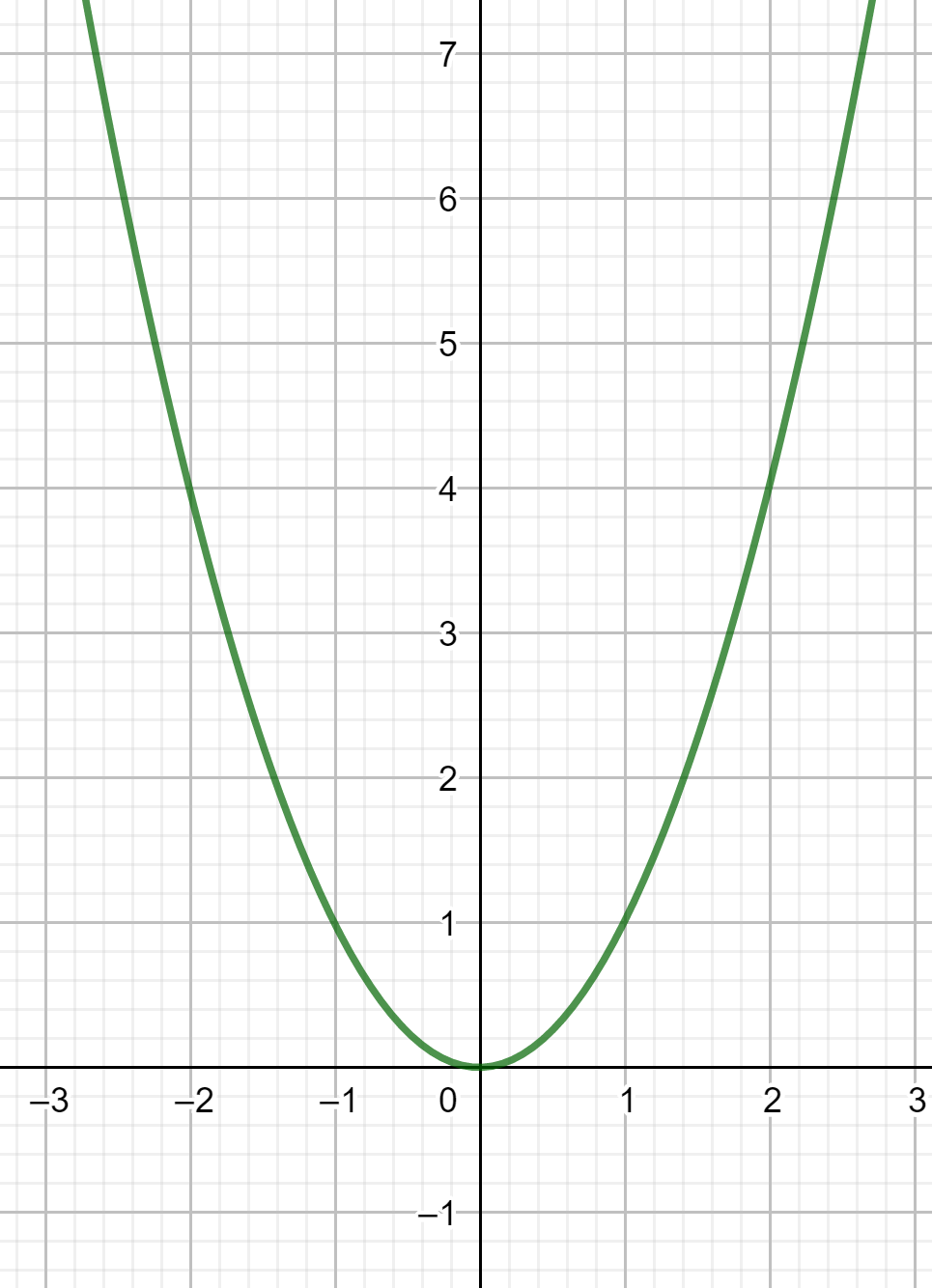
Sur ]-2.8;0], la courbe descend.

Sur [0;2.8[, la courbe monte.

représentation tableur

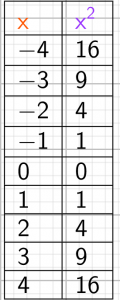
Les nombres négatifs et leurs carrés semblent varier en sens contraire.

Les nombres positifs et leurs carrés semblent varier dans le même sens.

représentation algébrique

f(x)=x^{2} définie sur  \mathbb{R}  

 

Sur \rbrack-\infty;0\rbrack, la fonction est décroissante.

si x_{1}<x_{2}\leq 0 alors x_{1}^{2}> x_{2}^{2}

Sur [0;+\infty[, la fonction est croissante.

si 0\leq x_{1}< x_{2} alors x_{1}^{2}< x_{2}^{2}

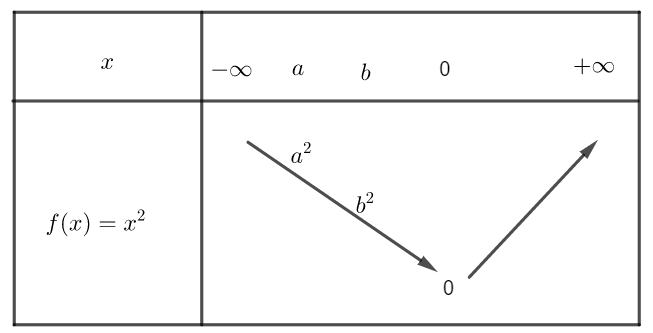
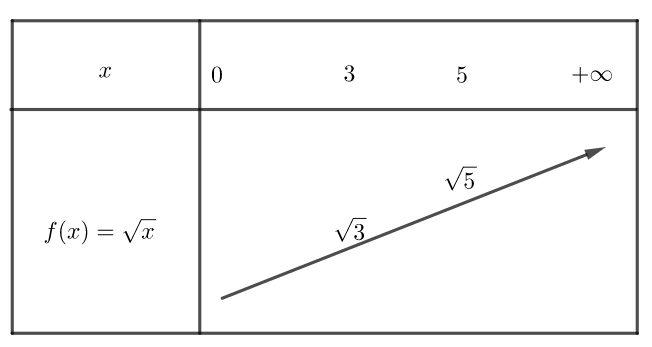
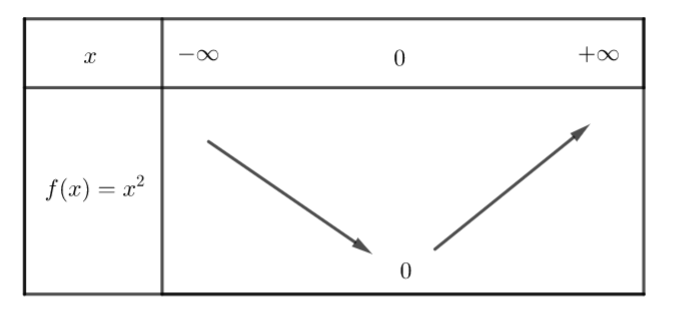
Voici le tableau de variation de la fonction carré sur \mathbb{R}  

a) Démontrer que la fonction carré est décroissante sur \rbrack-\infty;0\rbrack

Méthodes pour démontrer que f est décroissante
démonstration

b) Démontrer que la fonction carré est croissante sur [0;+\infty[

Méthodes pour démontrer que f est croissante
démonstration

Exercice n°2

 Sans calcul, comparer les réels suivants

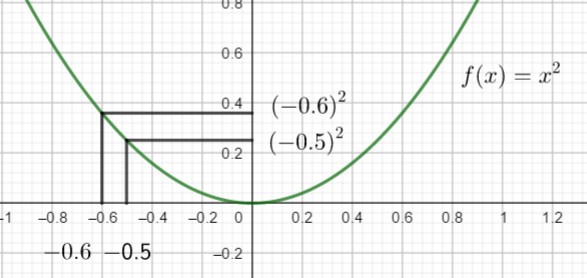
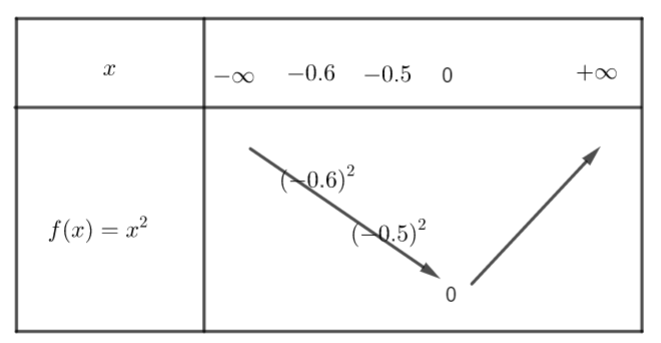
a) (-0.6)^{2} et {(-0.5)}^{2} .

conjecture avec la courbe d'une fonction
conjecture avec le tableau de variations d'une fonction
correction avec les variations d'une fonction

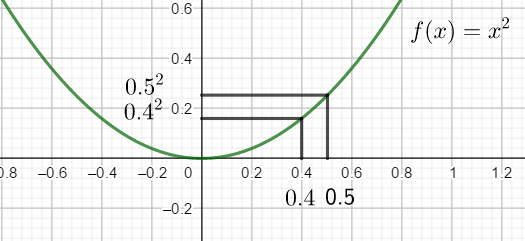
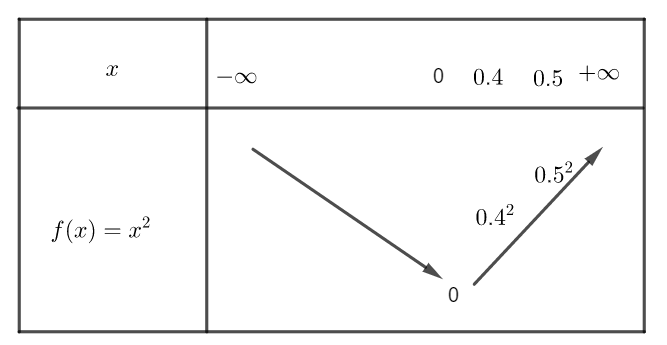
b) (0.4)^{2} et {(0.5)}^{2} .

conjecture avec la courbe d'une fonction
conjecture avec le tableau de variations d'une fonction
correction avec les variations d'une fonction

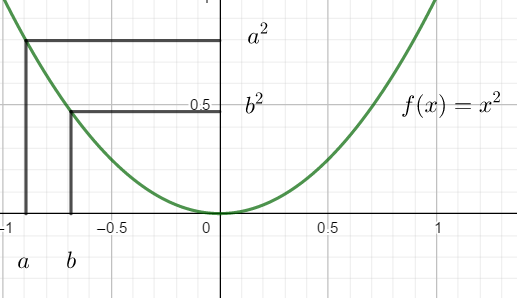
c) a^{2} et b^{2} avec  a<b<0 .

conjecture avec la courbe d'une fonction
conjecture avec le tableau de variations d'une fonction
correction avec les variations d'une fonction

la fonction cube

variations

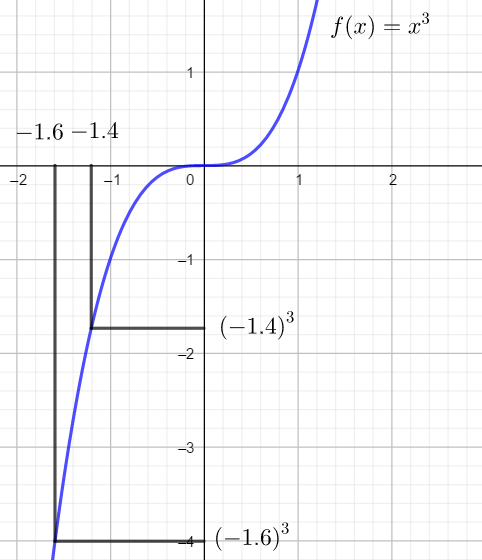
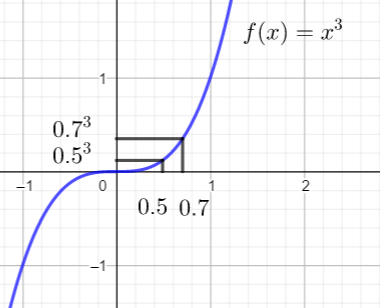
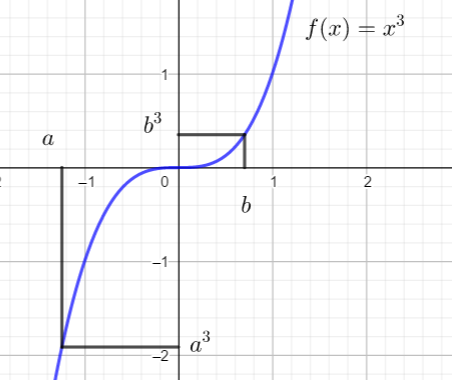
représentation graphique

2. représentation algébrique(1)1d

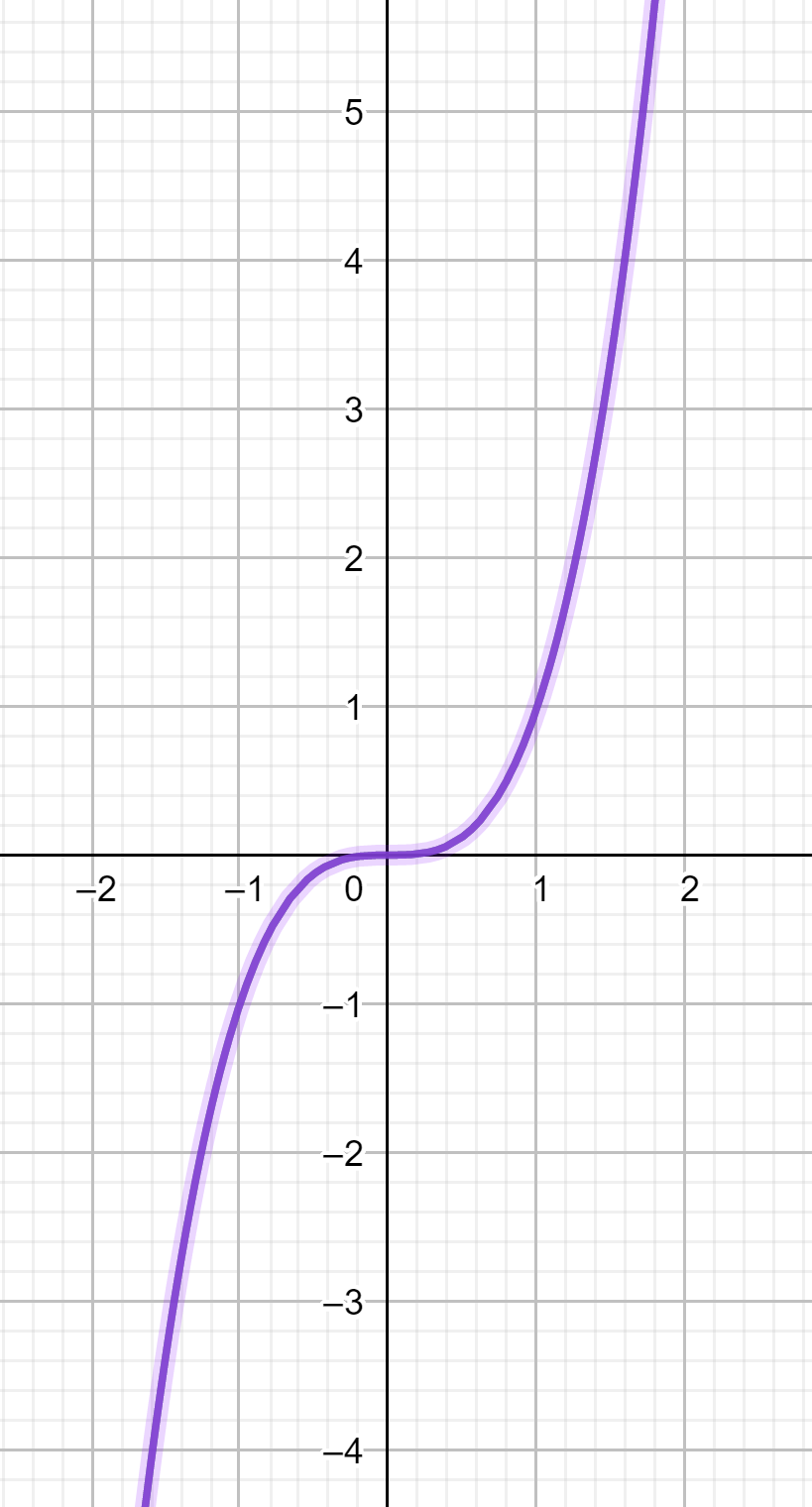
Sur [-1.6;1.8], la courbe monte.

représentation tableur

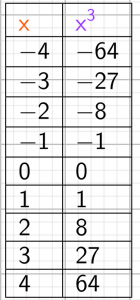
Les nombres  et leurs cubes semblent varier dans le même sens.

représentation algébrique

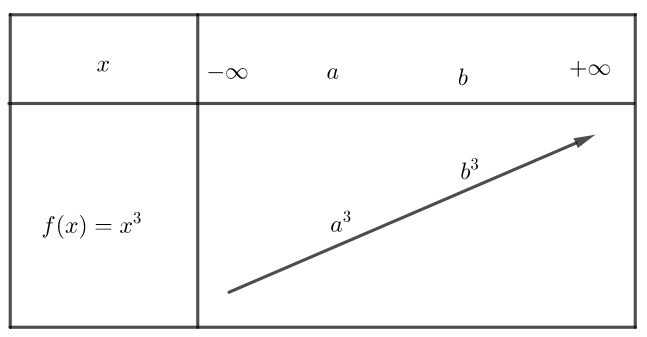
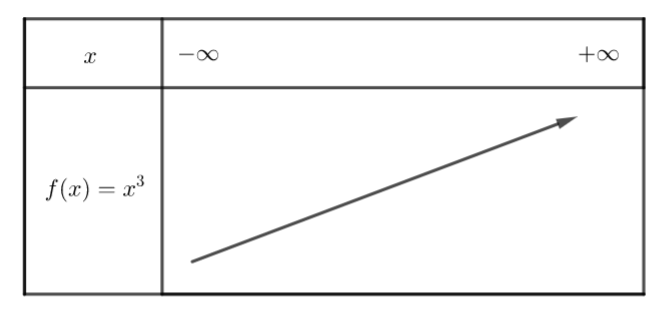
f(x)=x^{3} définie sur \mathbb{R}  

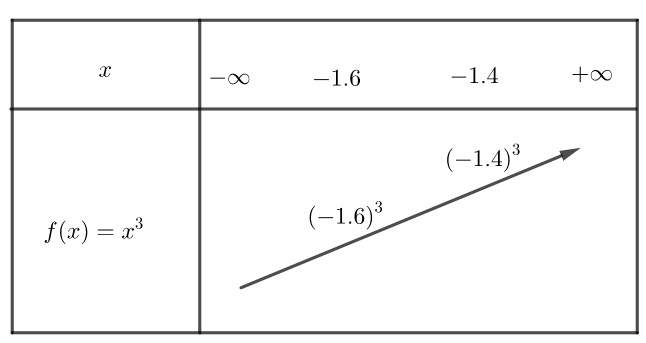
Sur ]-\infty;+\infty[, la fonction est croissante.

si x_{1}< x_{2} alors x_{1}^{3}< x_{2}^{3}

La démonstration des variations de la fonction cube n’est pas au programme, donc le résultat est admis.

Exercice n°3

 Sans calcul, comparer les réels suivants

a) (-1.6)^{3} et {(-1.4)}^{3} .

conjecture avec la courbe d'une fonction
conjecture avec le tableau de variations d'une fonction
correction avec les variations d'une fonction

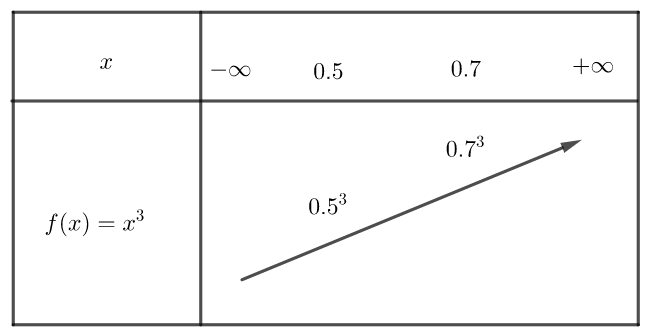
b) (0.5)^{3} et {(0.7)}^{3} .

conjecture avec la courbe d'une fonction
conjecture avec le tableau de variations d'une fonction
correction avec les variations d'une fonction

c) a^{3} et b^{3}  avec a<b 

conjecture avec la courbe d'une fonction
conjecture avec le tableau de variations d'une fonction
correction avec les variations d'une fonction

la fonction inverse

variations

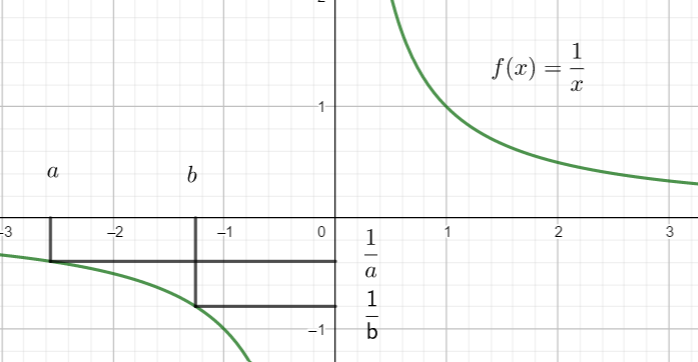
représentation graphique

2. représentation algébrique(1)1c

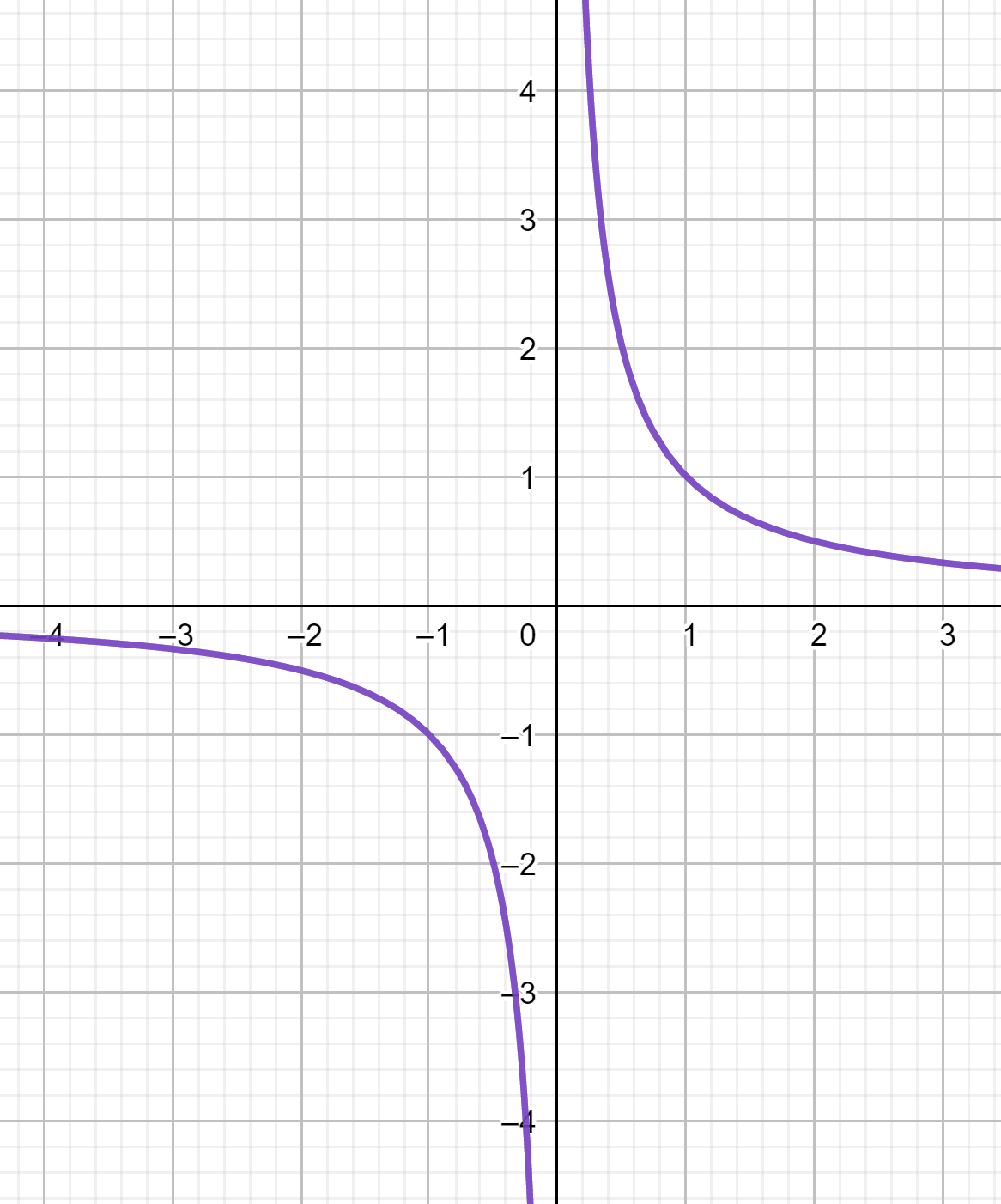
Sur [-4.4;0[, puis sur ]0;3.4]la courbe descend.

représentation tableur

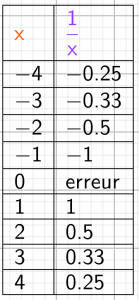
Les nombres négatifs et leurs inverses  semblent varier en sens contraire.

Les nombres positifs et leurs inverses  semblent varier en sens contraire.

représentation algébrique

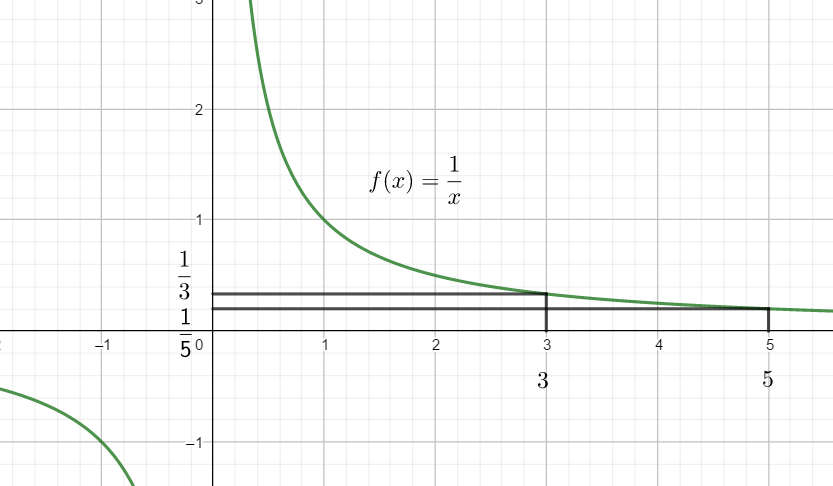
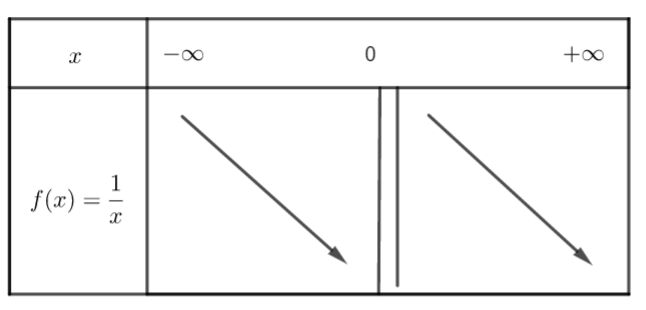
f(x)=\frac{1}{x} définie sur \mathbb{R}  privé de 0 .

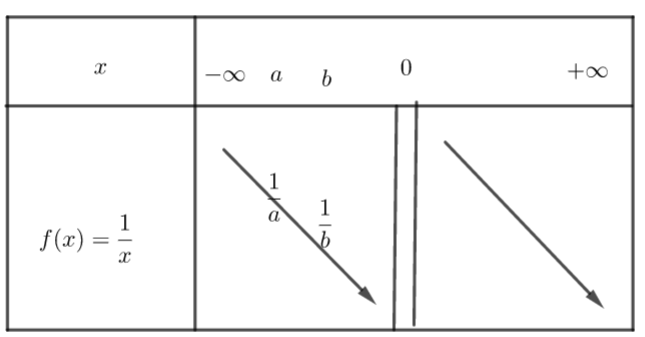
Sur ]-\infty;0[, la fonction est décroissante.

si x_{1}<x_{2}< 0 alors \frac{1}{x_{1}}> \frac{1}{x_{2}}

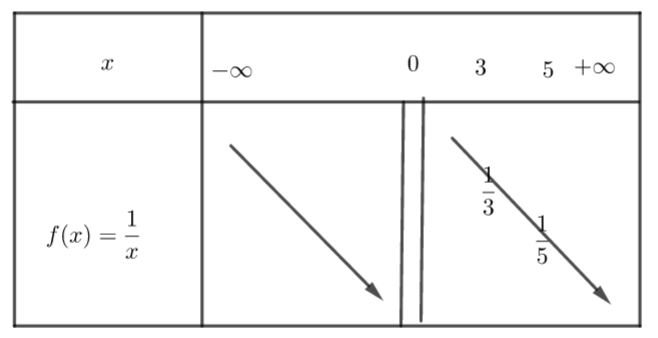
Sur ]0;+\infty[, la fonction est décroissante.

si 0\leq x_{1}< x_{2} alors \frac{1}{x_{1}}< \frac{1}{x_{2}}

a) Démontrer que la fonction inverse est décroissante sur ]-\infty;0[

démonstration

b) Démontrer que la fonction inverse est décroissante sur ]0;+\infty[

démonstration

Exercice n°4

 Sans calcul, comparer les réels suivants

a) \frac{1}{3} et \frac{1}{5} .

conjecture avec la courbe d'une fonction
conjecture avec le tableau de variations d'une fonction
correction avec les variations d'une fonction

b) \frac{1}{a} et \frac{1}{b} avec a<b<0 .

conjecture avec la courbe d'une fonction
conjecture avec le tableau de variations d'une fonction
correction avec les variations d'une fonction

la fonction racine carrée

variations

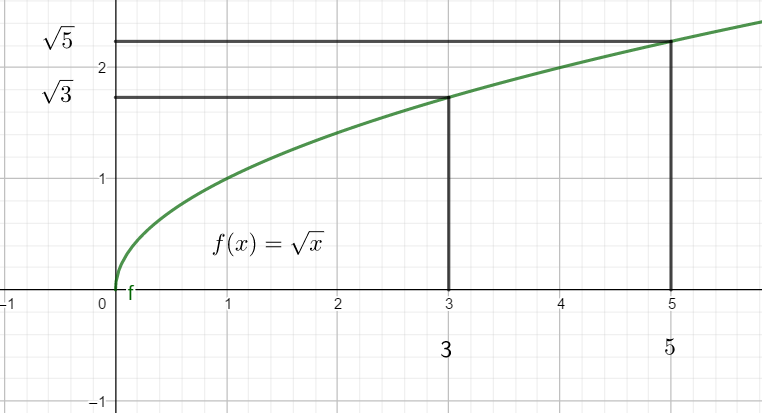
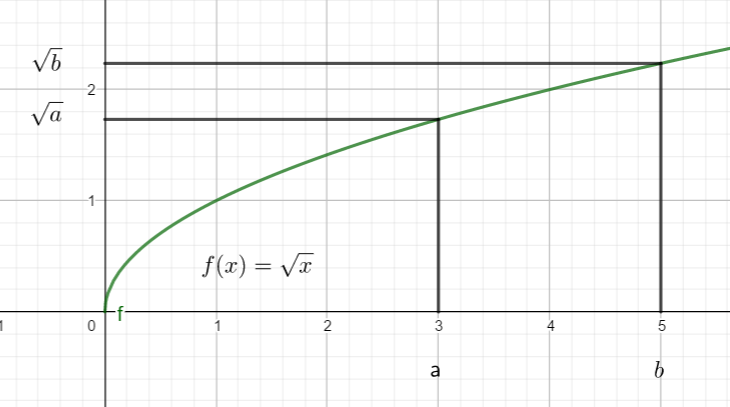
représentation graphique

2. représentation algébrique(1)1e

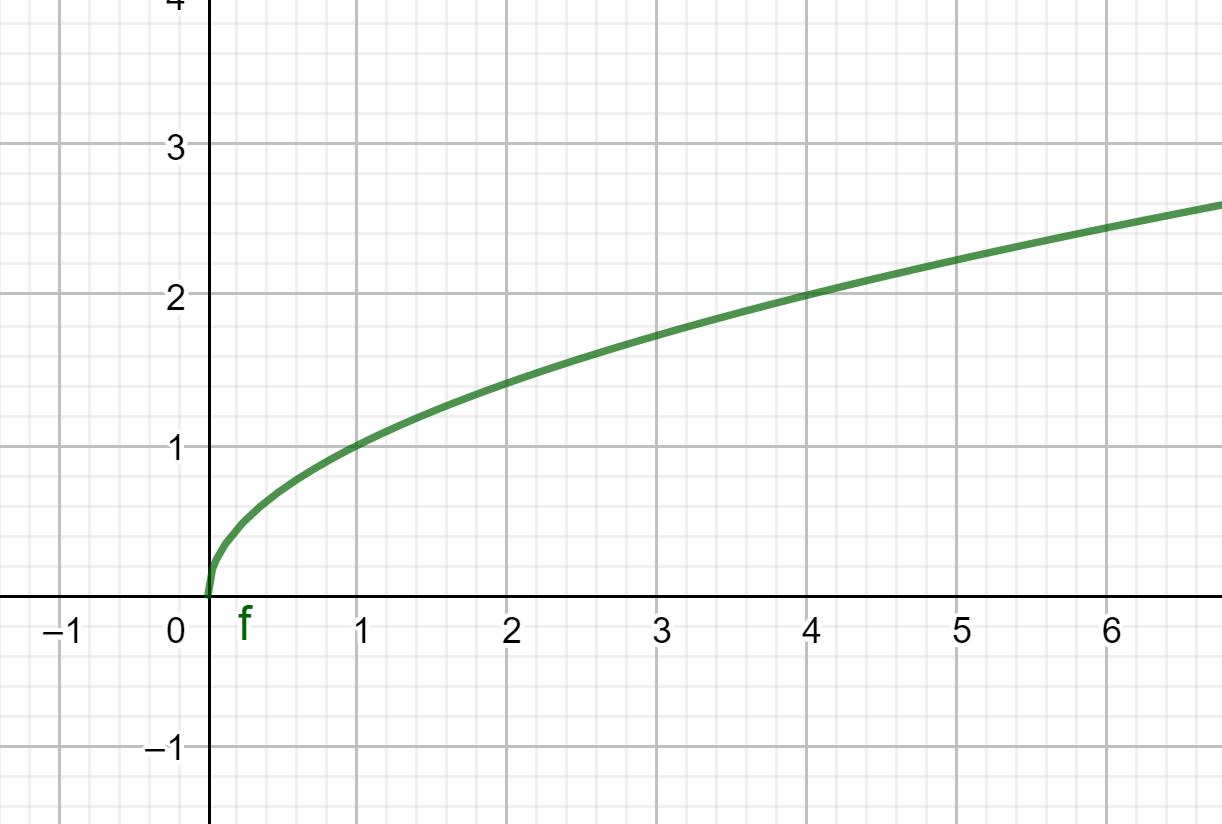
Sur [0;7], la courbe monte.

représentation tableur

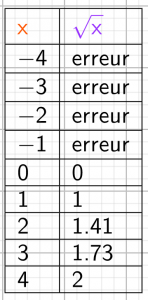
Les nombres positifs et leurs racines carré semblent varier dans le même sens.

représentation algébrique

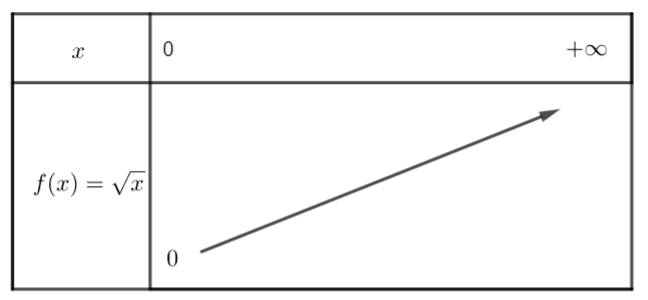
f(x)=\sqrt{x} définie sur [0;+\infty[

 

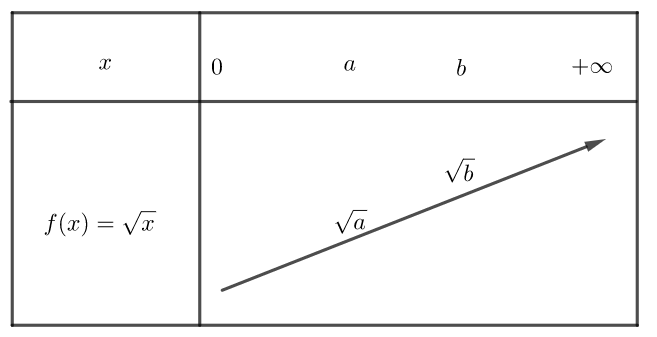
Sur [0;+\infty[, la fonction est croissante.

si 0\leq x_{1}< x_{2} alors \sqrt{x_{1}}< \sqrt{x_{2}}

Démontrer que la fonction racine carrée est croissante sur [0;+\infty[

Méthodes pour démontrer que f est croissante
démonstration

Exercice n°5

 Sans calcul, comparer les réels suivants

a) \sqrt{3} et \sqrt{5}

conjecture avec la courbe d'une fonction
conjecture avec le tableau de variations d'une fonction
correction avec les variations d'une fonction

b) \sqrt{a} et \sqrt{b} avec 0 \leq a<b 

conjecture avec la courbe d'une fonction
conjecture avec le tableau de variations d'une fonction
correction avec les variations d'une fonction

©2020 – Math’O karé SAS

 Méthode : signe de la différence.

En général,  x_{1}<x_{2}.

Pour montrer que f est croissante, il faut montrer que les nombres  x_{1};x_{2} et les images  f(x_{1});f(x_{2}) varient dans le même sens.

Donc que f(x_{1})<f(x_{2}) 

C’est-à-dire que f(x_{1})-f(x_{2}) est négatif.

 

 

Méthode : décomposition ( s’il n’y a qu’une fois  x à droite du signe égal dans f(x)= )

On décompose la séquence de calcul avec des opérateurs : additionner, soustraire, multiplier et diviser ou avec des fonctions de référence : fonction carré, fonction cube, fonction inverse et fonction racine carrée.

Lorsque a>0 il semble que la fonction f soit croissante sur \mathbf{R} 

Il faut maintenant le démontrer. Comme la lettre x n’apparaît qu’une fois à droite du signe = dans l’écriture  f(x)=ax+b, nous allons décomposer la séquence de calcul en utilisant des opérateurs : ajouter, soustraire, multiplier et diviser ou des fonctions de référence : carré, inverse, cube et racine carrée.

Montrons que la fonction f est croissante sur \mathbf{R}

On écrit en haut l’hypothèse . Puis on utilise la décomposition

x_{1}< x_{2}

On mutiplie par a qui est positif, le sens de l’inégalité ne change pas.

ax_{1}<ax_{2}.

On ajoute b, le sens de l’inégalité ne change pas.

ax_{1}+b< ax_{2}+b.

On écrit la conclusion.

f(x_{1})< f(x_{2})

Comme les nombres et les images varient dans le même sens, la fonction f est croissante sur \mathbf{R}

On suppose que x_{1}<x_{2}.

Calculons

f(x_{1})-f(x_{2})=(ax_{1}+b)-(ax_{2}+b)\\\hspace{2.1cm}=ax_{1}+b-ax_{2}-b\\\hspace{2.1cm}=ax_{1}-ax_{2}

Il est plus facile d’étudier le signe d’un produit que d’une somme. Donc on factorise.

\hspace{2.1cm}=a(x_{1}-x_{2})\\a est positif

x_{1}-x_{2} est négatif car x_{1}<x_{2}

Donc le produit a(x_{1}-x_{2}) est négatif

Donc f(x_{1})-f(x_{2})<0

Donc f(x_{1})<f(x_{2})

On a donc montré que les nombres  x_{1};x_{2} et les images f(x_{1});f(x_{2}) varient dans le même sens.

Donc f est croissante sur \mathbf{R}

 Méthode : signe de la différence.

En général x_{1}<x_{2} .

Pour montrer que f est décroissante, il faut montrer que les nombres x_{1}; x_{2} et f(x_{1}); f(x_{2}) varient en sens contraire.

Il faut donc montrer que  f(x_{1})>f(x_{2}) .

C’est à dire que f(x_{1})-f(x_{2}) est positif.

 

Méthode : décomposition ( s’il n’y a qu’une fois  x à droite du signe égal dans f(x)= )

On décompose la séquence de calcul avec des opérateurs : additionner, soustraire, multiplier et diviser ou avec des fonctions de référence : fonction carré, fonction cube, fonction inverse et fonction racine carrée.

Lorsque a<0 il semble que la fonction f soit décroissante sur \mathbf{R} 

Il faut maintenant le démontrer. Comme la lettre x n’apparaît qu’une fois à droite du signe = dans l’écriture  f(x)=ax+b, nous allons décomposer la séquence de calcul en utilisant des opérateurs : ajouter, soustraire, multiplier et diviser ou des fonctions de référence : carré, inverse, cube et racine carrée.

Montrons que la fonction f est décroissante sur \mathbf{R}

On écrit en haut l’hypothèse . Puis on utilise la décomposition

x_{1}< x_{2}

On mutiplie par a qui est négatif le sens de l’inégalité change .

ax_{1}> ax_{2}.

On ajoute b, le sens de l’inégalité ne change pas.

ax_{1}+b>ax_{2}+b.

On écrit la conclusion.

f(x_{1})> f(x_{2})

Comme les nombres et les images varient en sens contraire, la fonction f est décroissante sur \mathbf{R}

On suppose que x_{1}<x_{2}.

Calculons

f(x_{1})-f(x_{2})=(ax_{1}+b)-(ax_{2}+b)\\\hspace{2.1cm}=ax_{1}+b-ax_{2}-b\\\hspace{2.1cm}=ax_{1}-ax_{2}

Il est plus facile d’étudier le signe d’un produit que d’une somme. Donc on factorise.

\hspace{2.1cm}=a(x_{1}-x_{2})\\a est négatif

x_{1}-x_{2} est négatif car x_{1}<x_{2}

Donc le produit a(x_{1}-x_{2}) est positif

Donc f(x_{1})-f(x_{2})>0

Donc f(x_{1})>f(x_{2})

On a donc montré que les nombres  x_{1};x_{2} et les images f(x_{1});f(x_{2}) varient  en sens contraire.

Donc f est décroissante sur \mathbf{R}

{-0.5}\times{5.4}+7 et {-0.5}\times{4.6}+7 sont les images de 5.4 et de 4.6 par la fonction affine définie par

f(x)=-0.5x+7.

On peut conjecturer le résultat par lecture graphique.

En construisant graphiquement les images de 4.6 et 5.4 , on constate que l’image de 4.6 est située au-dessus de l’image de 5.4.

{-0.5}\times{4.6}+7>{-0.5}\times{5.4}+7

{-0.5}\times{5.4}+7 et {-0.5}\times{4.6}+7 sont les images de 5.4 et de 4.6 par la fonction affine définie par

latex]f(x)=-0.5x+7[/latex].

On utilise le tableau de variation ci-dessous :

On peut en déduire l’inégalité :

{-0.5}\times{4.6}+7>{-0.5}\times{5.4}+7

Pour comparer  {-0.5}\times{5.4}+7 et {-0.5}\times{4.6}+7 , on identifie la fonction f, les deux nombres x_{1} et x_{2}.

Ici f(x)=-0.5x+7 , x_{1}=4.6 et x_{2}=5.4.

{-0.5}\times{5.4}+7 et {-0.5}\times{4.6}+7 sont les images de 5.4 et de 4.6 par la fonction affine définie par f(x)=-0.5x+7.

Pour la fonction affine a=-0.5 donc f est décroissante.

On utilise si x_{1}<x_{2} alors  f(x_{1})>f(x_{2})

Comme 4.6<5.4 et commef est décroissante.On peut conclure que :

{-0.5}\times{4.6}+7>{-0.5}\times{5.4}+7

{2}\times{0.5}-4 et {2}\times{1.5}-4 sont les images de 0.5 et de 1.5 par la fonction affine définie par f(x)=2x-4.

On utilise la courbe de la fonction affine f définie par f(x)=2x-4. 

On constate que l’image de 0.5 est située en dessous de l’image de 1.5 .

Donc {2}\times{0.5}-4<{2}\times{1.5}-4

{2}\times{0.5}-4 et {2}\times{1.5}-4 sont les images de 0.5 et de 1.5 par la fonction affine définie par f(x)=2x-4.

On peut utiliser le tableau de variation ci-dessous:

On en déduit l’inégalité suivante :

{2}\times{0.5}-4<{2}\times{1.5}-4

Pour comparer  {2}\times{0.5}-4 et {2}\times{1.5}-4 , on identifie la fonction f, les deux nombres x_{1} et x_{2}.

Ici f(x)=2x-4 , x_{1}=0.5 et x_{2}=1.5.

{2}\times{0.5}-4 et {2}\times{1.5}-4 sont les images de 0.5 et de 1.5 par la fonction affine définie par f(x)=2x-4.

Pour la fonction affine a=2 donc f est croissante.

On utilise si x_{1}<x_{2} alors  f(x_{1})<f(x_{2})

Comme 0.5<1.5 et commef est croissante.On peut conclure que :

{2}\times{0.5}-4<{2}\times{1.5}-4

{0.25}\times{a}-4 et {0.25}\times{b}-4 sont les images de a et de b par la fonction affine définie par f(x)=0.25x-4.

De plus a<b, on place a et b n’importe où sur l’axe des abscisses tels que a soit le plus à gauche.

On utilise la représentation graphique de f(x)=0.25x-4.

L’image de a est située sous l’image de b donc

{0.25}\times{a}-4<{0.25}\times{b}-4

{0.25}\times{a}-4 et {0.25}\times{b}-4 sont les images de a et de b par la fonction affine définie par f(x)=0.25x-4.

On utilise le tableau de variations ci-dessous.

De plus a<b, on place a et b n’importe où sur la première ligne du tableau de variations tels que a soit le plus à gauche.

D’après le tableau de variations, on peut écrire :

{0.25}\times{a}-4<{0.25}\times{b}-4

Pour comparer  {0.25}\times{a}-4 et {0.25}\times{b}-4 , on identifie la fonction f, les deux nombres x_{1} et x_{2}.

Ici f(x)=0.25x-4 , x_{1}=a et x_{2}=b.

{0.25}\times{a}-4 et {0.25}\times{b}-4 sont les images de a et de b par la fonction affine définie par f(x)=0.25x-4.

Pour la fonction affine,  a=0.25 donc f est croissante.

On utilise si x_{1}<x_{2} alors  f(x_{1})<f(x_{2})

Comme a<b et commef est croissante.On peut conclure que :

{0.25}\times{a}-4<{0.25}\times{b}-4

On suppose que x_{1}<x_{2}.

Calculons

f(x_{1})-f(x_{2})=x_{1}^{2}-x_{2}^{2}

Il est plus facile d’étudier le signe d’un produit que d’une somme. Donc on factorise. On utilise l’identité remarquable a^{2}-b^{2}=(a-b)(a+b)

\hspace{2.1cm}=(x_{1}-x_{2})(x_{1}+x_{2})\\x_{1}-x_{2} est négatif car x_{1}<x_{2}\\x_{1}+x_{2} est négatif car x_{1} et x_{2} sont négatifs car ils appartiennent à ]-\infty;0]

Donc le produit (x_{1}-x_{2})(x_{1}+x_{2}) est positif

Donc f(x_{1})-f(x_{2})>0

Donc f(x_{1})>f(x_{2})

On a donc montré que les nombres  x_{1};x_{2} et les images f(x_{1});f(x_{2}) varient  en sens contraire.

Donc f est décroissante sur ]-\infty;0]

On suppose que x_{1}<x_{2}.

Calculons

f(x_{1})-f(x_{2})=x_{1}^{2}-x_{2}^{2}

Il est plus facile d’étudier le signe d’un produit que d’une somme. Donc on factorise. On utilise l’identité remarquable a^{2}-b^{2}=(a-b)(a+b)

\hspace{2.1cm}=(x_{1}-x_{2})(x_{1}+x_{2})\\x_{1}-x_{2} est négatif car x_{1}<x_{2}\\x_{1}+x_{2} est positif car x_{1} et x_{2} sont positifs car ils appartiennent à [0;+\infty[

Donc le produit (x_{1}-x_{2})(x_{1}+x_{2}) est négatif

Donc f(x_{1})-f(x_{2})<0

Donc f(x_{1})<f(x_{2})

On a donc montré que les nombres  x_{1};x_{2} et les images f(x_{1});f(x_{2}) varient dans le même sens.

Donc f est croissante sur [0;+\infty[

(-0.6)^{2} et (-0.5)^{2} sont les images de -0.6 et de -0.5 par la fonction  définie par f(x)=x^{2}.

Voici la courbe de f(x)=x^{2}.

L’image de -0.6 est au-dessus de l’image de -0.5 donc :

(-0.6)^{2}>(-0.5)^{2}

(-0.6)^{2} et (-0.5)^{2} sont les images de -0.6 et de -0.5 par la fonction affine définie par f(x)=x^{2}.

On utilise le tableau de variations suivant :

D’après le tableau de variations, on peut déduire :(-0.6)^{2}>(-0.5)^{2}

 

Pour comparer  (-0.6)^{2} et (-0.5)^{2} , on identifie la fonction f, les deux nombres x_{1} et x_{2}.

Ici f(x)=x^{2} , x_{1}=-0.6 et x_{2}=-0.5.

(-0.6)^{2} et (-0.5)^{2} sont les images de -0.6 et de -0.5 par la fonction définie par f(x)=x^{2}.

La fonction carré est décroissante sur ]-\infty;0].

On utilise si x_{1}<x_{2} alors  f(x_{1})>f(x_{2})

Comme -0.6<-0.5 et commef est décroissante.On peut conclure que :

(-0.6)^{2}>(-0.5)^{2}

0.4^{2} et 0.5^{2} sont les images de 0.4 et de 0.5 par la fonction définie par f(x)=x^{2}.

On utilise la représentation graphique de f(x)=x^{2}.

L’image de 0.4 est située en-dessous de l’image de 0.5 , donc

0.4^{2}<0.5^{2}

 

0.4^{2} et 0.5^{2} sont les images de 0.4 et de 0.5 par la fonction définie par f(x)=x^{2}.

On va utiliser le tableau de variations ci-dessous

On peut déduire du tableau de variation, l’inégalité suivante :

0.4^{2}<0.5^{2}

 

Pour comparer  0.4^{2} et 0.5^{2} , on identifie la fonction f, les deux nombres x_{1} et x_{2}.

Ici f(x)=x^{2} , x_{1}=0.4 et x_{2}=0.5.

0.4^{2} et 0.5^{2} sont les images de 0.4 et de 0.5 par la fonction définie par f(x)=x^{2}.

La fonction carré est croissante sur [0;+\infty[.

On utilise si x_{1}<x_{2} alors  f(x_{1})<f(x_{2})

Comme 0.4<0.5 et commef est croissante.On peut conclure que :

0.4^{2}<0.5^{2}

a^{2} et b^{2} sont les images de a et de b par la fonction définie par f(x)=x^{2}.

a et b sont négatifs et a<b. Je place a et b sur l’axe des abscisses à gauche de l’origine du repère avec a situé à gauche de  b

On va utiliser la courbe de f(x)=x^{2}.

L’image de a est située au dessus de celle de  b, donc

a^{2}>b^{2}

 

a^{2} et b^{2} sont les images de a et de b par la fonction définie par f(x)=x^{2}.

a et b sont négatifs et a<b. Je place a et b sur la première ligne du tableau de variations à gauche de zéro avec a situé à gauche de  b.

On utilise le tableau de variations ci-dessous:

On peut déduire du tableau de variations, l’inégalité suivante :

a^{2}>b^{2}

Pour comparer  a^{2} et b^{2} , on identifie la fonction f, les deux nombres x_{1} et x_{2}.

Ici f(x)=x^{2} , x_{1}=a et x_{2}=b.

a^{2} et b^{2} sont les images de a et de b par la fonction définie par f(x)=x^{2}.

a et  b sont négatifs.

La fonction carré est décroissante sur ]-\infty;0].

On utilise si x_{1}<x_{2} alors  f(x_{1})>f(x_{2})

Comme a<b et commef est décroissante.On peut conclure que :

a^{2}>b^{2}

(-1.6)^{3} et (-1.4)^{3} sont les images de -1.6 et de -1.4 par la fonction définie par f(x)=x^{3}.

On utilise la représentation graphique de f(x)=x^{3}.

L’image de -1.6 est en-dessous de l’image de -1.4 donc (-1.6)^{3}<(-1.4)^{3}

(-1.6)^{3} et (-1.4)^{3} sont les images de -1.6 et de -1.4 par la fonction définie par f(x)=x^{3}.

On utilise le tableau de variations ci-dessous:

D’après le tableau de variations, on peut écrire l’inégalité suivante : (-1.6)^{3}<(-1.4)^{3} 

Pour comparer  (-1.6)^{3} et (-1.4)^{3} , on identifie la fonction f, les deux nombres x_{1} et x_{2}.

Ici f(x)=x^{3} , x_{1}=-1.6 et x_{2}=-1.4.

(-1.6)^{3} et (-1.4)^{3} sont les images de -1.6 et de -1.4 par la fonction définie par f(x)=x^{3}.

La fonction cube est croissante sur \mathbf{R}.

On utilise si x_{1}<x_{2} alors  f(x_{1})<f(x_{2})

Comme -1.6<-1.4 et commef est croissante.On peut conclure que :

(-1.6)^{3}<(-1.4)^{3}

0.5^{3} et 0.7^{3} sont les images de 0.5 et de 0.7 par la fonction définie par f(x)=x^{3}.

On utilise la représentation graphique de f(x)=x^{3}.

L’image de 0.5 est en-dessous de  l’image de 0.7 donc

0.5^{3}<0.7^{3} 

 

0.5^{3} et 0.7^{3} sont les images de 0.5 et de 0.7 par la fonction définie par f(x)=x^{3}.

On utilise le tableau de variation ci-dessous :

D’après le tableau de variation, on en déduit l’inégalité suivante  0.5^{3}<0.7^{3} 

Pour comparer  0.5^{3} et 0.7^{3} , on identifie la fonction f, les deux nombres x_{1} et x_{2}.

Ici f(x)=x^{3} , x_{1}=0.5 et x_{2}=0.7.

0.5^{3} et 0.7^{3} sont les images de 0.5 et de 0.7 par la fonction définie par f(x)=x^{3}.

La fonction cube est croissante sur \mathbf{R}.

On utilise si x_{1}<x_{2} alors  f(x_{1})<f(x_{2})

Comme 0.5<0.7 et commef est croissante.On peut conclure que :

0.5^{3}<0.7^{3}

a^{3} et b^{3} sont les images de a et de b par la fonction définie par f(x)=x^{3}.

On utilise la représentation graphique de f(x)=x^{3}.

L’image de a est située en-dessous de l’image de b, donc a^{3}<b^{3} 

a^{3} et b^{3} sont les images de a et de b par la fonction définie par f(x)=x^{3}.

On utilise le tableau de variation suivant :

On peut déduire du tableau de variation, l’inégalité suivante :a^{3}<b^{3}

Pour comparer  a^{3} et b^{3} , on identifie la fonction f, les deux nombres x_{1} et x_{2}.

Ici f(x)=x^{3} , x_{1}=a et x_{2}=b.

a^{3} et b^{3} sont les images de a et de b par la fonction définie par f(x)=x^{3}.

La fonction cube est croissante sur \mathbf{R}.

On utilise si x_{1}<x_{2} alors  f(x_{1})<f(x_{2})

Comme a<b et commef est croissante.On peut conclure que :

a^{3}<b^{3}

On suppose que x_{1}<x_{2}.

Calculons

f(x_{1})-f(x_{2})=\frac{1}{x_{1}}-\frac{1}{x_{2}}

Il est plus facile d’étudier le signe d’un quotient que d’une somme. Donc on met au même dénominateur, icix_{1}.x_{2}  .

\hspace{2.1cm}={\frac{1}{x_{1}}}\times{\frac{x_{2}}{x_{2}}}-{\frac{1}{x_{2}}}\times{\frac{x_{1}}{x_{1}}}\\\hspace{2.1cm}=\frac{x_{2}-x_{1}}{x_{1}x_{2}}\\x_{2}-x_{1} est positif car x_{1}<x_{2} donc x_{2}>x_{1}\\x_{1}x_{2} est positif car c’est le produit de x_{1} et x_{2} qui sont négatifs car ils appartiennent à ]-\infty;0[

Donc le quotient \frac{x_{2}-x_{1}}{x_{1}x_{2}} est positif

Donc f(x_{1})-f(x_{2})>0

Donc f(x_{1})>f(x_{2})

On a donc montré que les nombres  x_{1};x_{2} et les images f(x_{1});f(x_{2}) varient  en sens contraire.

Donc f est décroissante sur ]-\infty;0[

On suppose que x_{1}<x_{2}.

Calculons

f(x_{1})-f(x_{2})=\frac{1}{x_{1}}-\frac{1}{x_{2}}

Il est plus facile d’étudier le signe d’un quotient que d’une somme. Donc on met au même dénominateur, icix_{1}.x_{2}  .

\hspace{2.1cm}={\frac{1}{x_{1}}}\times{\frac{x_{2}}{x_{2}}}-{\frac{1}{x_{2}}}\times{\frac{x_{1}}{x_{1}}}\\\hspace{2.1cm}=\frac{x_{2}-x_{1}}{x_{1}x_{2}}\\x_{2}-x_{1} est positif car x_{1}<x_{2} donc x_{2}>x_{1}\\x_{1}x_{2} est positif car c’est le produit de x_{1} et x_{2} qui sont positifs car ils appartiennent à ]0;+\infty[

Donc le quotient \frac{x_{2}-x_{1}}{x_{1}x_{2}} est positif

Donc f(x_{1})-f(x_{2})>0

Donc f(x_{1})>f(x_{2})

On a donc montré que les nombres  x_{1};x_{2} et les images f(x_{1});f(x_{2}) varient  en sens contraire.

Donc f est décroissante sur ]-\infty;0[

\frac{1}{3} et \frac{1}{5} sont les images de 3 et de 5 par la fonction définie par f(x)=\frac{1}{x}.

On utilise la représentation graphique de f(x)=\frac{1}{x}.

L’image de 3 est située au-dessus de l’image de 5 donc:

\frac{1}{3}>\frac{1}{5}

 

\frac{1}{3} et \frac{1}{5} sont les images de 3 et de 5 par la fonction définie par f(x)=\frac{1}{x}.

On utilise le tableau de variations ci-dessous :

On peut déduire du tableau de variation l’inégalité suivante :

\frac{1}{3}>\frac{1}{5}

Pour comparer  \frac{1}{3} et \frac{1}{5} , on identifie la fonction f, les deux nombres x_{1} et x_{2}.

Ici f(x)=\frac{1}{x} , x_{1}=3 et x_{2}=5.

\frac{1}{3} et \frac{1}{5} sont les images de 3 et de 5 par la fonction définie par f(x)=\frac{1}{x}.

3 et  5 sont positifs.

La fonction inverse est décroissante sur ]0;+\infty[.

On utilise si x_{1}<x_{2} alors  f(x_{1})>f(x_{2})

Comme 3<5 et commef est décroissante.On peut conclure que :

\frac{1}{3}>\frac{1}{5}

\frac{1}{a} et \frac{1}{b} sont les images de a et de b par la fonction définie par f(x)=\frac{1}{x}.

On utilise la représentation graphique de la fonction définie par f(x)=\frac{1}{x}.

L’image de a est située au-dessus de l’image de b , donc

\frac{1}{a}>\frac{1}{b}

 

\frac{1}{a} et \frac{1}{b} sont les images de a et de b par la fonction définie par f(x)=\frac{1}{x}.

On va utiliser le tableau de variation suivant:

On peut déduire du tableau de variation l’inégalité suivante :

\frac{1}{a}>\frac{1}{b}

Pour comparer  \frac{1}{a} et \frac{1}{b} , on identifie la fonction f, les deux nombres x_{1} et x_{2}.

Ici f(x)=\frac{1}{x} , x_{1}=a et x_{2}=b.

\frac{1}{a} et \frac{1}{b} sont les images de a et de b par la fonction définie par f(x)=\frac{1}{x}.

a et  b sont négatifs.

La fonction inverse est décroissante sur ]-\infty;0[.

On utilise si x_{1}<x_{2} alors  f(x_{1})>f(x_{2})

Comme a<b et commef est décroissante.On peut conclure que :

\frac{1}{a}>\frac{1}{b}

On suppose que x_{1}<x_{2}.

Calculons

f(x_{1})-f(x_{2})=\sqrt{x_{1}}-\sqrt{x_{2}}

On va multiplier \sqrt{x_{1}}-\sqrt{x_{2}} par \frac{\sqrt{x_{1}}+\sqrt{x_{2}}}{\sqrt{x_{1}}+\sqrt{x_{2}}}.Puis on utilise l’identité remarquable (a-b)(a+b)=a^{2}-b^{2}

\hspace{2.1cm}=(\sqrt{x_{1}}-\sqrt{x_{2}})\frac{\sqrt{x_{1}}+\sqrt{x_{2}}}{\sqrt{x_{1}}+\sqrt{x_{2}}}\\\hspace{2.1cm}=\frac{(\sqrt{x_{1}}-\sqrt{x_{2}})(\sqrt{x_{1}}+\sqrt{x_{2}})}{\sqrt{x_{1}}+\sqrt{x_{2}}}\\\hspace{2.1cm}=\frac{\sqrt{x_{1}}^{2}-\sqrt{x_{2}}^{2}}{\sqrt{x_{1}}+\sqrt{x_{2}}}\\\hspace{2.1cm}=\frac{x_{1}-x_{2}}{\sqrt{x_{1}}+\sqrt{x_{2}}}\\x_{1}-x_{2} est négatif car x_{1}<x_{2}\\\sqrt{x_{1}}+\sqrt{x_{2}} est positif car la somme de deux racines carrées qui sont positives , est positive.

Donc \frac{x_{1}-x_{2}}{\sqrt{x_{1}}+\sqrt{x_{2}}} est négatif.

Donc f(x_{1})-f(x_{2})<0

Donc f(x_{1})<f(x_{2})

On a donc montré que les nombres  x_{1};x_{2} et les images f(x_{1});f(x_{2}) varient dans le même sens.

Donc f est croissante sur [0;+\infty[

\sqrt{3} et \sqrt{5} sont les images de 3 et de 5 par la fonction définie par f(x)=\sqrt{x}.

On utilise la représentation graphique de la fonction définie par f(x)=\sqrt{x}.

L’image de 3 est située en-dessous de l’image de 5  donc \sqrt{3}<\sqrt{5}

\sqrt{3} et \sqrt{5} sont les images de 3 et de 5 par la fonction définie par f(x)=\sqrt{x}.

On utilise le tableau de variation suivant :

D’après le tableau de variations , on peut en déduire l’inégalité suivante :

\sqrt{3}<\sqrt{5}

Pour comparer  \sqrt{3} et \sqrt{5} , on identifie la fonction f, les deux nombres x_{1} et x_{2}.

Ici f(x)=\sqrt{x} , x_{1}=3 et x_{2}=5.

\sqrt{3} et \sqrt{5} sont les images de 3 et de 5 par la fonction définie par f(x)=\sqrt{x}.

La fonction racine carrée est croissante sur [0;+\infty[.

On utilise si x_{1}<x_{2} alors  f(x_{1})<f(x_{2})

Comme 3<5 et commef est croissante.On peut conclure que :

\sqrt{3}<\sqrt{5}

\sqrt{a} et \sqrt{b} sont les images de a et de b par la fonction définie par f(x)=\sqrt{x}.

On utilise la courbe représentative de la fonction définie par f(x)=\sqrt{x}.

L’image de a est située en-dessous de l’image de b donc

\sqrt{a}<\sqrt{b}

\sqrt{a} et \sqrt{b} sont les images de a et de b par la fonction définie par f(x)=\sqrt{x}.

On utilise le tableau de variations ci-dessous:

D’après le tableau de variations, on peut en déduire l’inégalité suivante

\sqrt{a}<\sqrt{b}

Pour comparer  \sqrt{a} et \sqrt{b} , on identifie la fonction f, les deux nombres x_{1} et x_{2}.

Ici f(x)=\sqrt{x} , x_{1}=a et x_{2}=b.

\sqrt{a} et \sqrt{b} sont les images de a et de b par la fonction définie par f(x)=\sqrt{x}.

La fonction racine carrée est croissante sur [0;+\infty[.

On utilise si x_{1}<x_{2} alors  f(x_{1})<f(x_{2})

Comme a<b et commef est croissante.On peut conclure que :

\sqrt{a}<\sqrt{b}

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.