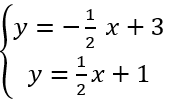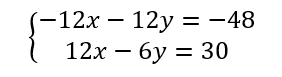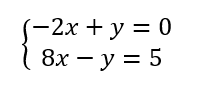Sommaire
Résoudre graphiquement un système de deux équations à deux inconnues.
Exemple n°1
Résoudre graphiquement le système de deux équations a deux inconnues suivant :
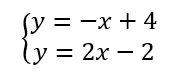
On trace les deux droites dans le repère avec la méthode de son choix. Par exemple en utilisant ordonnée à l’origine et coefficient directeur.
Dans y=-x+4 on détermine le coefficient directeur a=-1 et l’ordonnée à l’origine b=4 .
On place 4 sur l’axe des ordonnées. A partir du point de coordonnées (0;4) , j’avance horizontalement de 1 vers la droite et je descends de 1 (a=-1 ). J’obtiens alors le deuxième point. Je trace ensuite la droite qui passe par les deux points.
Dans y=2x-2 on détermine le coefficient directeur a=2 et l’ordonnée à l’origine b=-2 .
On place -2 sur l’axe des ordonnées. A partir du point de coordonnées (0;-2) , j’avance horizontalement de 1 vers la droite et je monte de 2 (a=2 ). J’obtiens alors le deuxième point. Je trace ensuite la droite qui passe par les deux points.
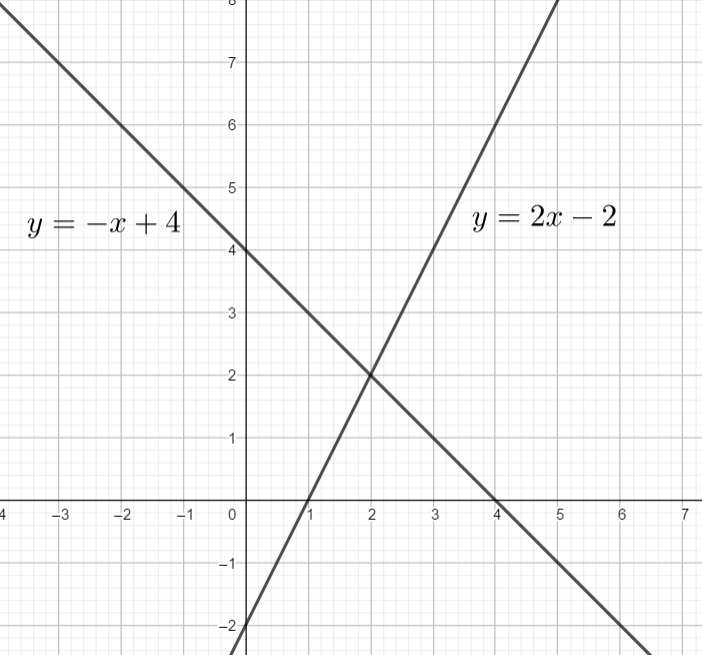
Le point d’intersection des deux droites a pour coordonnées (2;2) .
Le couple solution du système est (2;2).
Exemple n°2
Résoudre graphiquement le système de deux équations a deux inconnues suivant :
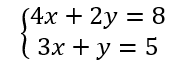
Il faut d’abord transformer les deux équations pour obtenir deux équations de la forme y=ax+b
Dans l’équation 4x+2y=8 , 4x n’est pas à sa place. C’est un terme dans une somme. On enlève 4x de chaque côté.
2y=-4x+8Dans l’équation précédente, le 2 n’est pas à sa place. C’est un facteur dans un produit. Je divise par 2 de chaque côté.
y=\frac{-4x+8}{2}\\y=\frac{-4x}{2}+\frac{8}{2}\\y=-2x+4Dans l’équation 3x+y=5 , 3x n’est pas à sa place. C’est un terme dans une somme. On enlève 3x de chaque côté.
y=-3x+5On obtient alors un système similaire à celui de l’exercice n°1.
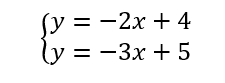
On trace les deux droites dans le repère avec la méthode de son choix. Par exemple en utilisant ordonnée à l’origine et coefficient directeur.
Dans y=-2x+4 on identifie le coefficient directeur a=-2 et l’ordonnée à l’origine b=4 . On place 4 sur l’axe des ordonnées. A partir du point de coordonnées (0;4), j’avance horizontalement de 1 vers la droite et je descends de 2 (a=-2 ). J’obtiens alors le deuxième point. Je trace ensuite la droite qui passe par les deux points.
Dans y=-3x+5 on identifie le coefficient directeur a=-3 et l’ordonnée à l’origine b=5 . On place 5 sur l’axe des ordonnées. A partir du point de coordonnées (0;5), j’avance horizontalement de 1 vers la droite et je descends de 3 (a=-3 ). J’obtiens alors le deuxième point. Je trace ensuite la droite qui passe par les deux points.
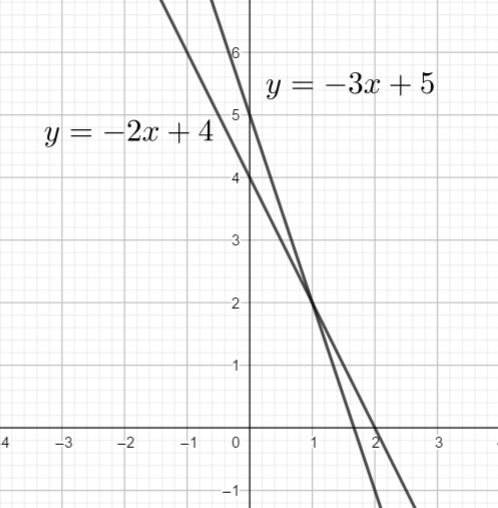
Le point d’intersection des deux droites a pour coordonnées (1;2) .
Le couple-solution du système est (1;2).
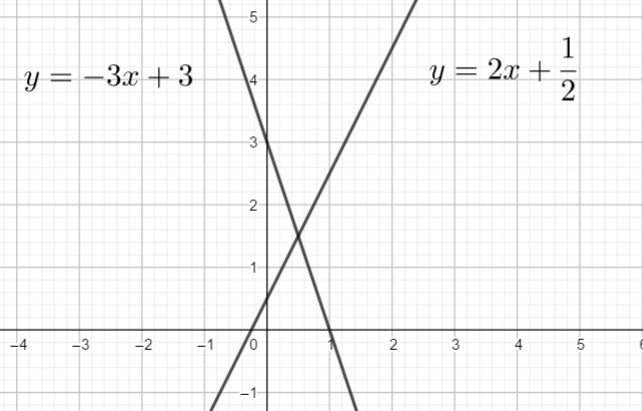
Exercice n°1
Résoudre graphiquement le système suivant :
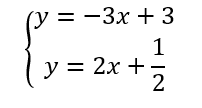
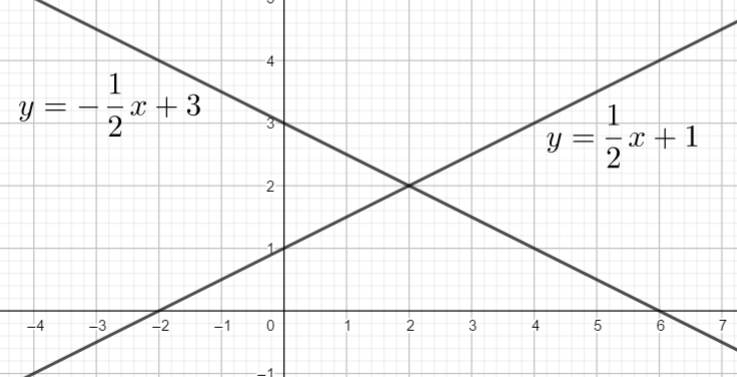
Exercice n°2
Résoudre graphiquement le système suivant :
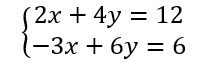
Résoudre , par substitution , un système de deux équations à deux inconnues.
Exemple n°3
Résoudre, par le calcul, le système de deux équations a deux inconnues suivant :
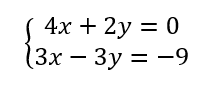
L’objectif est d’éliminer une des deux inconnues pour obtenir une équation à une seule inconnue. Je choisis d’éliminer y.
A l’aide de la 1ère équation, j’exprime y en fonction de x.
2y=-4x\\y=-\frac{4x}{2}\\y=-2xJe remplace y par (-2x) par entre parenthèses dans la deuxième équation pour obtenir une équation du premier degré à une seule inconnue :
3x-3(-2x)=-9Pour la résoudre, il faut mettre à leur place, les membres qui ne sont pas à leur place.
3x+6x=-9\\9x=-9\\x=-\frac{9}{9}\\x=-1Pour déterminer y , je remplace x par -1 dans ,par exemple, la première équation.
{4}\times{(-1)}+2y=0\\-4+2y=0\\2y=4\\y=\frac{4}{2}\\y=2Le couple solution est (-1;2)
Valider le résultat avec l’application Calcul Formel de Géogébra.
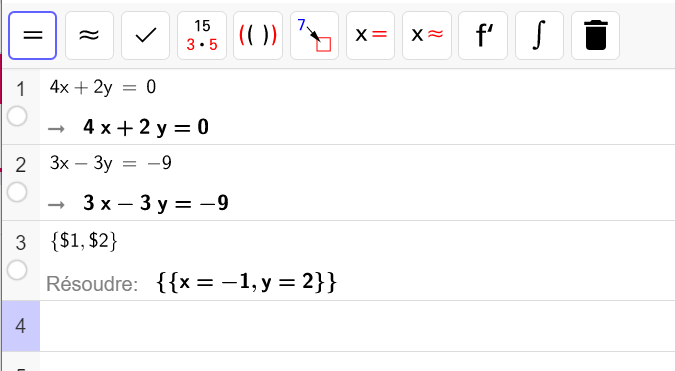
Saisir 4x+2y=0 sur la ligne 1 et saisir 3x-3y=-9 sur la ligne 2.
Sur la ligne 3, cliquer gauche sur la ligne 2 puis sur la ligne 1 en maintenant le clic durant l’opération et cliquer ensuite sur l’onglet X=.
On voit apparaître le couple solution du système.
Exercice n°3
Résoudre, par le calcul et par substitution, le système de deux équations à deux inconnues suivant :
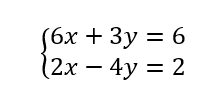
Valider vos calculs avec la fenêtre Géogébra ci-dessous :
Exercice n°4
Résoudre, par le calcul et par substitution, le système de deux équations à deux inconnues suivant :
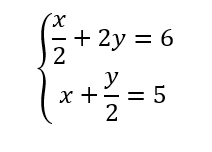
Valider vos calculs avec la fenêtre Géogébra ci-dessous :
Résoudre , par combinaison linéaire , un système de deux équations à deux inconnues.
Exemple n°4
Résoudre, par le calcul , le système de deux équations à deux inconnues suivant :
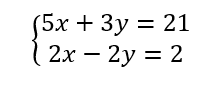
Je décide d’éliminer les x , pour cela je dois multiplier la première équation par 2 et la deuxième équation par -5.
Ainsi on aura 10x dans la nouvelle première équation et son opposé -10x dans la nouvelle deuxième équation.
ATTENTION : quand on dit que je dois multiplier la première équation par 2 , je multiplie tout par 2
quand on dit que je dois multiplier la deuxième équation par -5 , je multiplie tout par-5 .
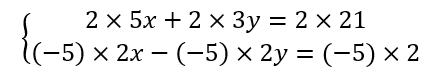
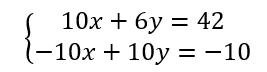
J’ajoute membre à membre ces deux égalités (les x disparaissent, ce qui était le but recherché)
6y+10y=42-10\\16y=32\\y=\frac{32}{16}\\y=2Pour déterminer la valeur de x je remplace y par 2 dans par exemple la première équation.
5x+{3}\times{2}=21\\5x+6=21\\5x=21-6\\5x=15\\x=\frac{15}{5}\\x=3Le couple solution est (3;2)
Valider le résultat avec l’application Calcul Formel de Géogébra.
Saisir 5x+3y=21 sur la ligne 1, valider.
Saisir 2x-2y=2 sur la ligne 2, valider.
Sur la ligne 3, cliquer gauche sur la ligne 2 puis sur la ligne 1 en maintenant le clic durant l’opération et cliquer ensuite sur l’onglet X=.
On voit apparaître le couple solution du système.

Exercice n°5
Résoudre, par le calcul et par combinaison linéaire, le système de deux équations à deux inconnues suivant :
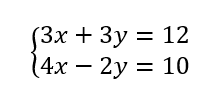
Valider vos calculs avec la fenêtre Géogébra ci-dessous :
Exercice n°6
Résoudre, par le calcul et par combinaison linéaire, le système de deux équations à deux inconnues suivant :
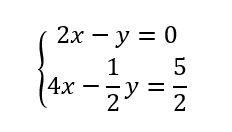
Valider vos calculs avec la fenêtre Géogébra ci-dessous :