Sommaire
Exemple n°1
résoudre par le calcul l’inéquation suivante dans \mathbf{R} (2x+1)^{2}<9.
Conjecture graphique ( on ne prouve rien, on se fait une idée du résultat).
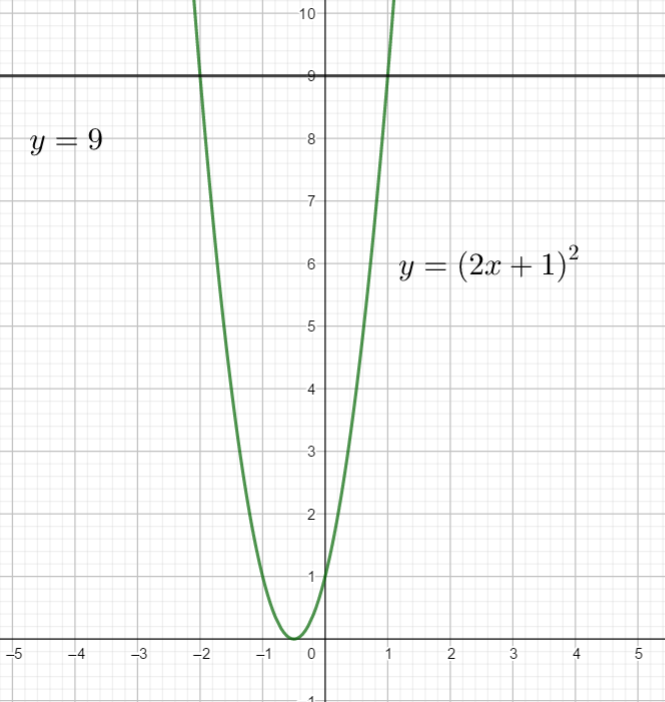
La courbe est sous la droite d’équation y=9 pour x strictement compris entre -2 et 1 . C’est à dire que S=]-2;1[ .
Résolvons dans \mathbf{R}, l’inéquation suivante (2x+1)^{2}<9
L’inéquation à résoudre (2x+1)^{2}<9 est du 2nd degré car en développant (2x+1)^{2} le plus grand exposant de x est 2.
La méthode proposée concerne les inéquations du second degré.
(2x+1)^{2}<91.Je fais tout passer à gauche, zéro apparaît à droite.
le 9 à droite du signe égal n’est pas à sa place, j’enlève 9 de chaque côté.
(2x+1)^{2}-9<02. Je factorise le membre de gauche.
a. Il n’y a pas de facteur commun.
b. J’utilise l’identité remarquable a^{2}-b^{2}=(a-b)(a+b) pour factoriser (2x+1)^{2}-9\\a^{2}=(2x+1)^{2} \hspace{2cm}a=(2x+1)\\b^{2}=9\hspace{3.2cm}b=3
Je remplace a et b par (2x+1) et 3 dans a^{2}-b^{2}=(a-b)(a+b)\\((2x+1)-3)((2x+1)+3)<0\\(2x-2)(2x+4)<0
3. J’écris la phrase d’introduction.
Je cherche pour quelles valeurs de x, le produit (2x-2)(2x+4) est de signe(-).
4. Je prépare mon tableau de signes.
Je résous 2x-2=0\\2x=2\\x=\frac{2}{2}\\x=1
Je résous 2x+4=0\\2x=-4\\x=\frac{-4}{2}\\x=-2
Je place les valeurs -2 et 1 sur la première ligne du tableau en les rangeant dans le bon ordre. Je place les zéros sur les lignes en-dessous.

Je remplis ce tableau avec des signes (-), (+) , des zéros et parfois des doubles barres quand il y a des valeurs interdites.
On utilise le résultat du cours suivant :

Sur la ligne du facteur (2x-2), comme a=2 , on commence par le signe (-) jusqu’au zéro et on complète avec des (+).
Sur la ligne du facteur (2x+4), comme a=2 , on commence par le signe (-) jusqu’au zéro et on complète avec des (+).
Pour compléter la ligne du produit (2x-2)(2x+4), j’applique la règle des signes pour le produit.
plus par plus : plus.
plus par moins : moins.
moins par plus : moins.
moins par moins : plus.

5. Je réponds à la phrase d’introduction.
Le produit (2x-2)(2x+4) est de signe(-) pour la deuxième colonne qui correspond aux valeurs de x comprises entre -2 et 1.
Je ne prends pas les valeurs -2 et 1 car le produit ne peut pas être nul. Donc j’ouvre les crochets en -2 et 1, ce qui signifie que les crochets sont tournés vers l’extérieur.
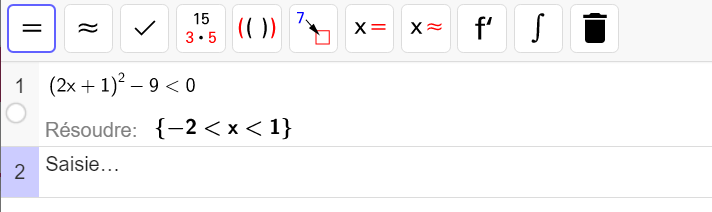
S=]-2;1[On vérifie à l’aide de l’application calcul formel de géogébra :
Exercice n°1
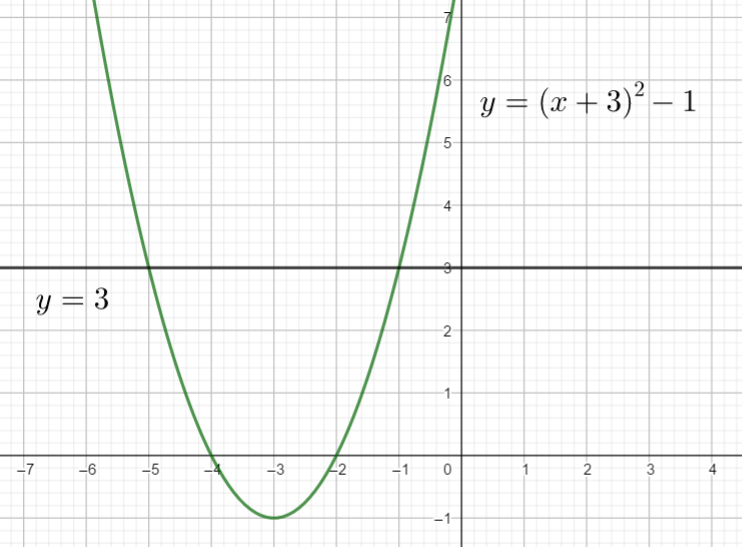
résoudre par le calcul l’inéquation suivante dans \mathbf{R}\\(x+3)^{2}-1\leq 3.
Pour valider la réponse obtenue, utiliser la fenêtre Géogébra ci-dessous. Sur la ligne 1 saisir (x+3)^{2}-1\leq 3 puis cliquer sur le septième onglet en haut en partant de la gauche . Sur la ligne suivante apparaît Réponse :
Pour saisir \leq taper < suivi de =
Exercice n°2
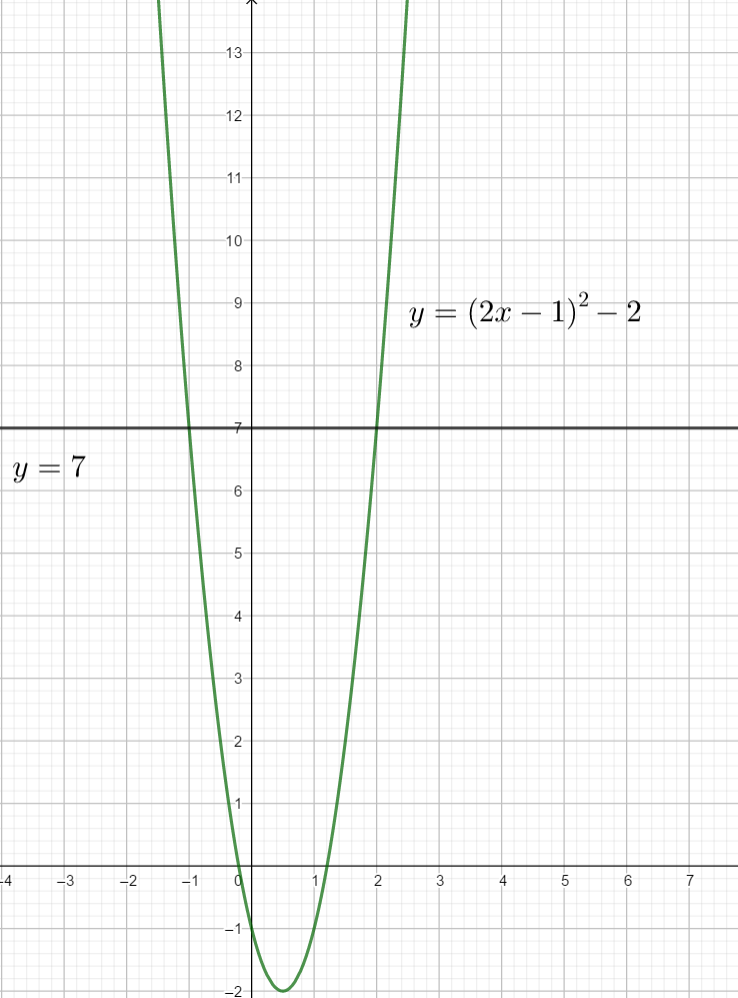
résoudre par le calcul l’inéquation suivante dans \mathbf{R}\\(2x-1)^{2}-2>7.
Pour valider la réponse obtenue, utiliser la fenêtre Géogébra ci-dessous. Sur la ligne 1 saisir (2x-1)^{2}-2>7 puis cliquer sur le septième onglet en haut en partant de la gauche . Sur la ligne suivante apparaît Réponse :
Exemple n°2
résoudre par le calcul l’inéquation suivante dans \mathbf{R}\\(x+2)(-x+4)\geq 0.
Conjecture graphique ( on ne prouve rien, on se fait une idée du résultat).
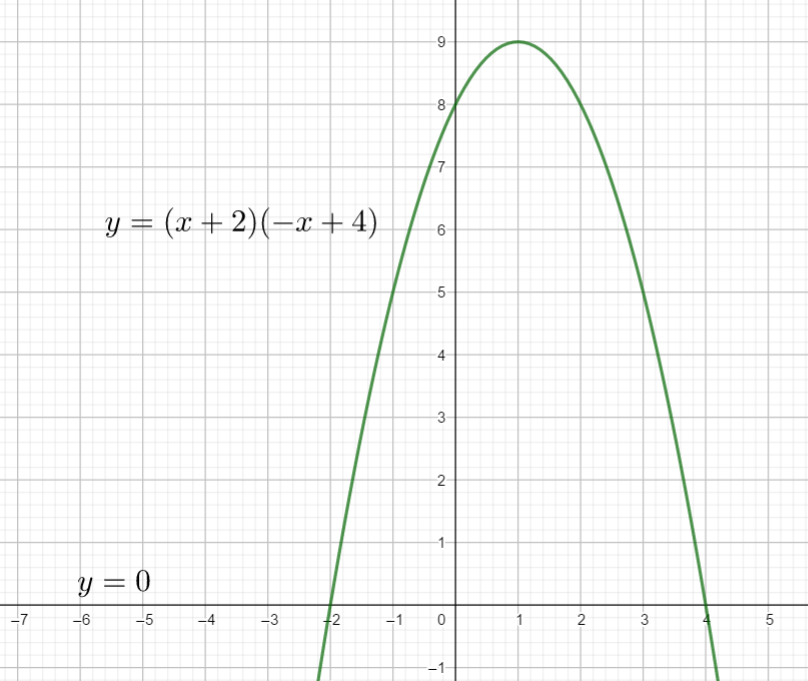
La courbe est au-dessus ou sur la droite d’équation y=0 pour x compris entre -2 et 4 . C’est à dire que S=[-2;4] .
Résolvons dans \mathbf{R}, l’inéquation suivante (x+2)(-x+4)\geq 0
L’inéquation à résoudre (x+2)(-x+4)\geq0 est du 2nd degré car en développant (x+2)(-x+4) le plus grand exposant de x est 2.
La méthode proposée concerne les inéquations du second degré.
(x+2)(-x+4)\geq0
1.Je ne fais pas tout passer à gauche, car zéro est déjà à droite.
2. Je ne factorise pas le membre de gauche, c’est déjà un produit de facteurs.
3. J’écris la phrase d’introduction.
Je cherche pour quelles valeurs de x, le produit (x+2)(-x+4) est de signe (+) ou nul.
4. Je prépare mon tableau de signes.
Je résous x+2=0\\x=-2
Je résous -x+4=0\\-x=-4\\x=4
Je place les valeurs -2 et 4 sur la première ligne du tableau en les rangeant dans le bon ordre. Je place les zéros sur les lignes en-dessous.
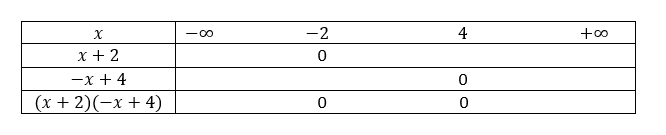
Je remplis ce tableau avec des signes (-), (+) , des zéros et parfois des doubles barres quand il y a des valeurs interdites.
On utilise le résultat du cours suivant :

Sur la ligne du facteur (x+2), comme a=1 , on commence par le signe (-) jusqu’au zéro et on complète avec des (+).
Sur la ligne du facteur (-x+4), comme a=-1 , on commence par le signe (+) jusqu’au zéro et on complète avec des (-).
Pour compléter la ligne du produit (2x-2)(2x+4), j’applique la règle des signes pour le produit.
plus par plus : plus.
plus par moins : moins.
moins par plus : moins.
moins par moins : plus.

5. Je réponds à la phrase d’introduction.
Le produit (x+2)(-x+4) est de signe(+) ou nul pour la deuxième colonne qui correspond aux valeurs de x comprises entre -2 et 4.
Je prends les valeurs -2 et 4 car le produit peut être nul. Donc je ferme les crochets en -2 et 4, ce qui signifie que les crochets sont tournés vers l’intérieur.
S=[-2;4]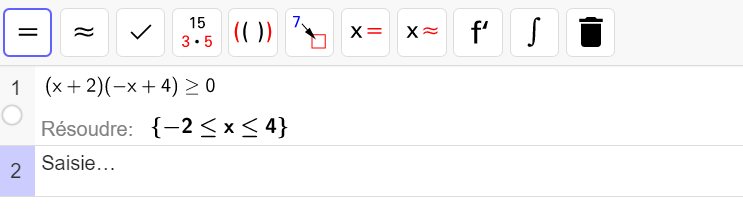
Exercice n°3
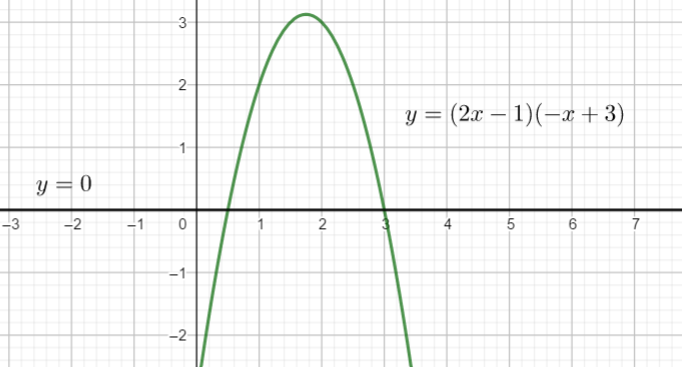
résoudre par le calcul l’inéquation suivante dans \mathbf{R}\\(2x-1)(-x+3)\leq 0.
Conjecture graphique ( on ne prouve rien, on se fait une idée du résultat).
Pour valider la réponse obtenue, utiliser la fenêtre Géogébra ci-dessous. Sur la ligne 1 saisir (2x-1)(-x+3)\leq 0 puis cliquer sur le septième onglet en haut en partant de la gauche . Sur la ligne suivante apparaît Réponse :
Pour saisir \leq taper < suivi de =
Exercice n°4
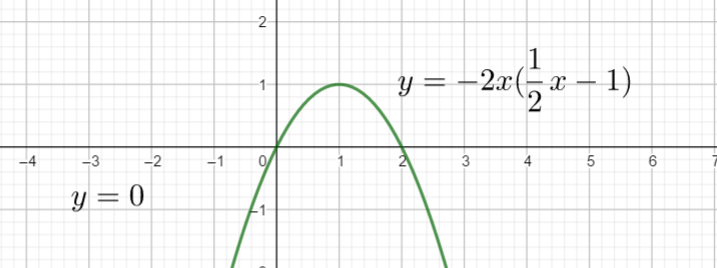
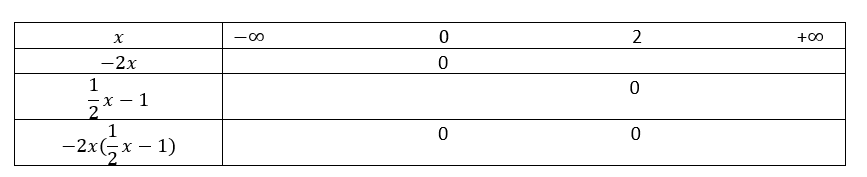
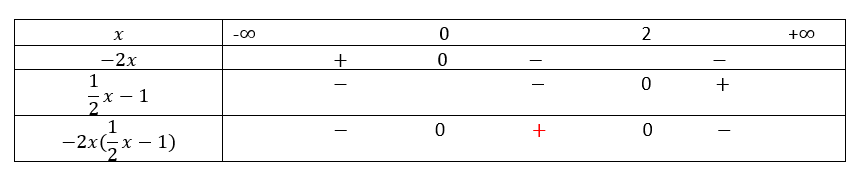
résoudre par le calcul l’inéquation suivante dans \mathbf{R}\\-2x(\frac{1}{2}x-1)> 0.
Conjecture graphique ( on ne prouve rien, on se fait une idée du résultat).
Pour valider la réponse obtenue, utiliser la fenêtre Géogébra ci-dessous. Sur la ligne 1 saisir -2x(\frac{1}{2}x-1)> 0 puis cliquer sur le septième onglet en haut en partant de la gauche . Sur la ligne suivante apparaît Réponse :
Pour saisir \leq taper < suivi de =
Exemple n°3
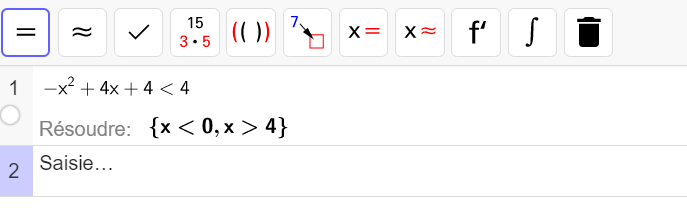
résoudre par le calcul l’inéquation suivante dans \mathbf{R}\\-x^{2}+4x+4<4.
Conjecture graphique ( on ne prouve rien, on se fait une idée du résultat).
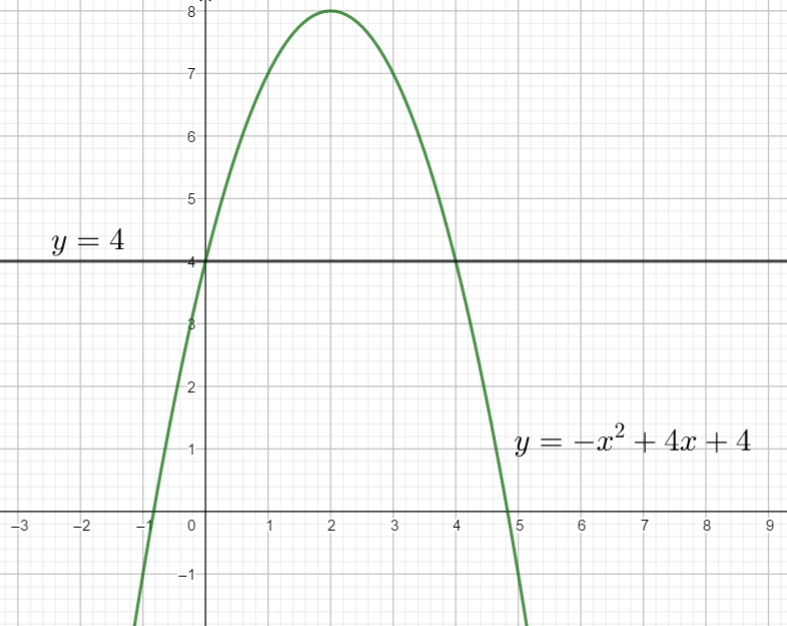
La courbe est sous la droite d’équation y=4 pour x compris entre -1.2 et 0 puis entre 4 et 5.2 . C’est à dire que S=[-1.2;0[\cup]4;5.2] .
Résolvons dans \mathbf{R}, l’inéquation suivante -x^{2}+4x+4<4.
L’inéquation à résoudre -x^{2}+4x+4<4 est du 2nd degré car le plus grand exposant de x est 2.
La méthode proposée concerne les inéquations du second degré.
-x^{2}+4x+4<4.
1.Je fais tout passer à gauche, zéro apparaît à droite.
le 4 à droite du signe égal n’est pas à sa place, j’enlève 4 de chaque côté.
-x^{2}+4x+4-4<0\\-x^{2}+4x<02. Je factorise le membre de gauche.
a. Il y a un facteur commun, ici c’est x.
-x^{2}={x}\times{(-x)}\\4x={x}\times{4}\\x(-x+4)<03. J’écris la phrase d’introduction.
Je cherche pour quelles valeurs de x, le produit x(-x+4) est de signe(-).
4. Je prépare mon tableau de signes.
Je résous x=0
Je résous -x+4=0\\-x=-4\\x=4
Je place les valeurs 0 et 4 sur la première ligne du tableau en les rangeant dans le bon ordre. Je place les zéros sur les lignes en-dessous.

Je remplis ce tableau avec des signes (-), (+) , des zéros et parfois des doubles barres quand il y a des valeurs interdites.
On utilise le résultat du cours suivant :

Sur la ligne du facteur x, comme a=1 , on commence par le signe (-) jusqu’au zéro et on complète avec des (+).
Sur la ligne du facteur (-x+4), comme a=-1 , on commence par le signe (+) jusqu’au zéro et on complète avec des (-).
Pour compléter la ligne du produit x(-x+4), j’applique la règle des signes pour le produit.
plus par plus : plus.
plus par moins : moins.
moins par plus : moins.
moins par moins : plus.

5. Je réponds à la phrase d’introduction.
Le produit x(-x+4) est de signe(-) pour la première colonne et la troisième colonne qui correspond aux valeurs de x comprises entre -\infty et 0 puis entre 4 et +\infty .
Je ne prends pas les valeurs 0 et 4 car le produit ne peut pas être nul. Donc j’ouvre les crochets en 0 et 4, ce qui signifie que les crochets sont tournés vers l’extérieur.
S=]-\infty;0[\cup]4;+\infty[ .
Exercice n°5
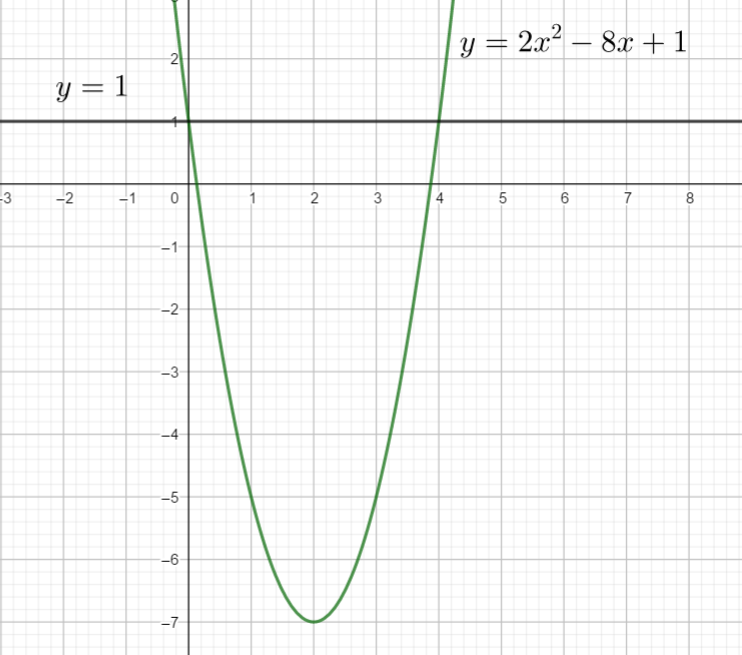
Résoudre par le calcul l’inéquation suivante dans \mathbf{R}\\2x^{2}-8x+1\leq 1.
Conjecture graphique ( on ne prouve rien, on se fait une idée du résultat).
Pour valider la réponse obtenue, utiliser la fenêtre Géogébra ci-dessous. Saisir 2x^{2}-8x+1\leq 1 puis cliquer sur le onglet en haut en partant de la gauche . Sur la ligne suivante apparaît Réponse :
Exercice n°6
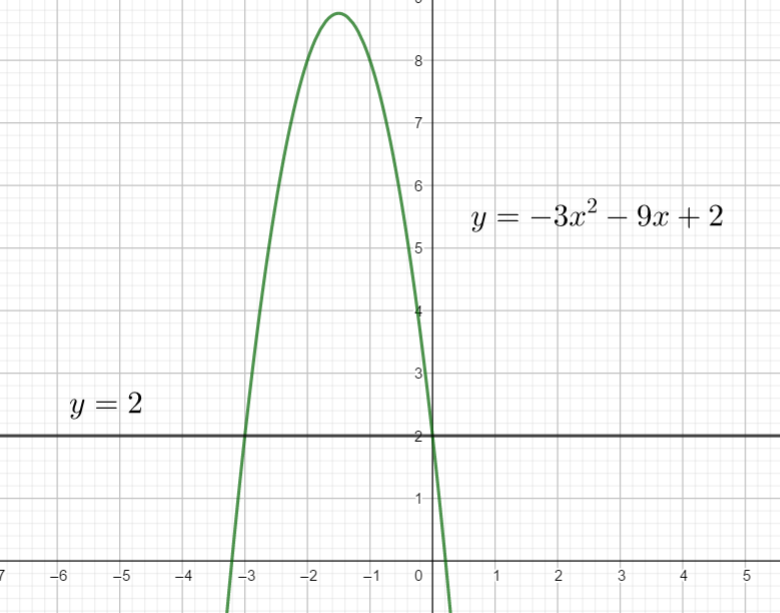
résoudre par le calcul l’inéquation suivante dans \mathbf{R}\\-3x^{2}-9x+2>2.
Conjecture graphique ( on ne prouve rien, on se fait une idée du résultat).
Pour valider la réponse obtenue, utiliser la fenêtre Géogébra ci-dessous. Saisir -3x^{2}-9x+2>2 puis cliquer sur le septième onglet en haut en partant de la gauche . Sur la ligne suivante apparaît Réponse :