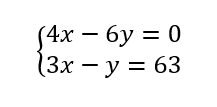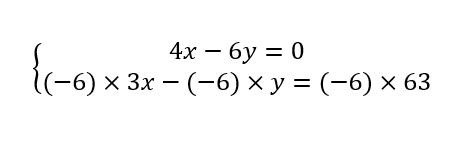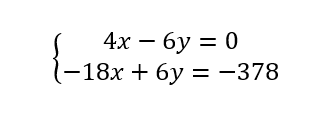Enoncé du problème:
« J’ai trois fois l’âge que vous aviez quand j’avais l’âge que vous avez.
Quand vous aurez l’âge que j’ai, nous aurons ensemble soixante trois ans.
Quel âge ai-je ?»
- Identification de ou des inconnue(s) .
2.Traduire les phrases de l’énoncé en langage mathématique en utilisant x et y , le cas échéant .
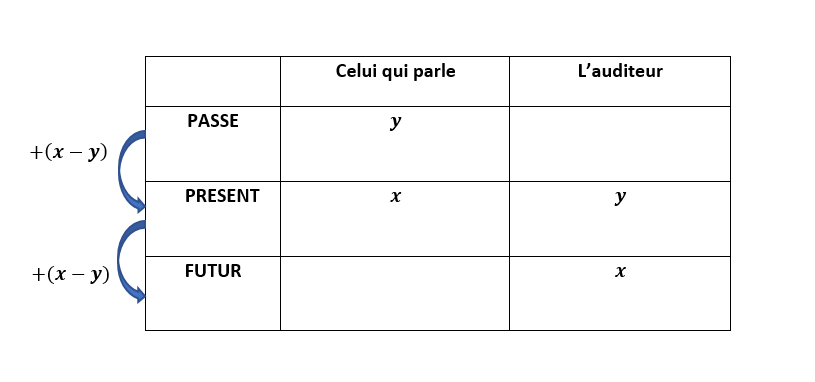
a) Il y a trois temps : le passé, le présent et le futur. Il y a deux personnes : celui qui parle et l’auditeur.
Compléter les pointillés du tableau suivant en fonction de x et de y en utilisant
Les résultats de la partie1: Identification de ou des inconnue(s) .
« j’avais l’âge que vous avez »
« vous aurez l’âge que j’ai »
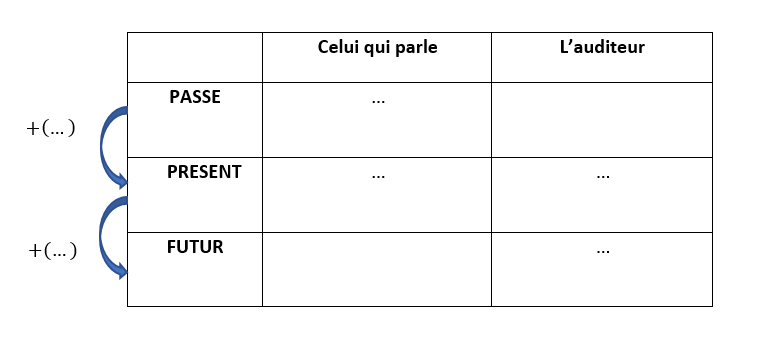
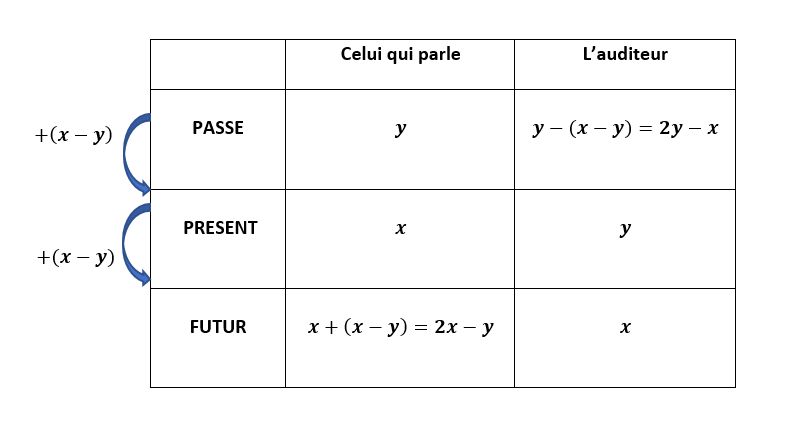
b) Pour déterminer l’âge de celui qui parle au futur et l’âge de l’auditeur au passé, utiliser le nombre d’années qui se sont écoulées entre le passé et le présent et entre le présent et le futur. .
3. Mise en équation du problème .
a. Traduire par une égalité mathématique la phrase : J’ai trois fois l’âge que vous aviez.
b. Traduire par une égalité mathématique la phrase : nous aurons ensemble soixante trois ans .
c. En déduire le système de deux équations à deux inconnues à résoudre.
4. Résolution du système d’équations.
5. Répondre au problème posé .