2.coordonnées d’un point . Exercices

Géométrie, Niveau seconde, Repères du plan : milieu d’un segment, distance entre deux points

Exercice n°1:

Dans chaque cas, déterminer par le calcul , les coordonnées de $I$ le milieu de $[AB]$

On peut conjecturer les coordonnées du milieu $I$ en utilisant la fenêtre géogébra ci-dessous. Pour cela on déplacera les points $A$ et $B$ en cliquant sur le premier onglet ( la flèche) et en sélectionnant Déplacer dans le menu déroulant. On n’hésitera pas à bouger le repère en cliquant sur le 11ème onglet et en sélectionnant Déplacer graphique dans le menu déroulant.

a) $A(2;1)$ et $B(-6;0)$

b) $A(5;3)$ et $B(-1;-6)$

c) $A(\frac{1}{2};-5)$ et $B(-\frac{3}{4};2)$

d) $A(0;\frac{1}{5})$ et $B(-1;\frac{1}{3})$

Exercice n°2 :

Déterminer si $ABCD$ est un parallélogramme dans chaque cas. Vous justifierez votre réponse à l’aide de calculs.

$A(-1;2)$ , $B(3;0)$ , $C(0;-2)$ et $D(-4;-1)$ .

2. $A(2;5)$ , $B(-1;4)$ , $C(-2;-3)$ et $D(1;-2)$ .

Exercice n°3 :

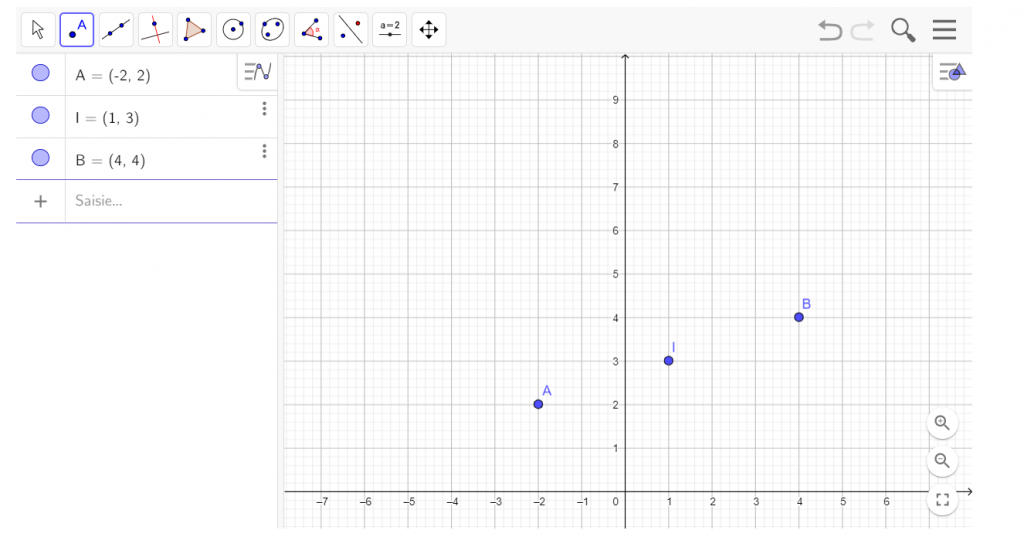
Soient $A(-2;2)$ et $I(1;3)$ dans le repère orthonormé ci-dessous.

On appelle $B$ le point tel que $I$ soit le milieu de $[AB]$ .

Placer $B$ dans le repère et lire graphiquement ses coordonnées.

2. Nous allons déterminer les coordonnées du point $B$ par le calcul. Comme on ne les connaît pas, on les note $(x;y)$ .

a. Parmi les deux propositions, quelle est la bonne ?

Proposition 1 : $x_B=\frac{x_A+x_I}{2}$ et $y_B=\frac{y_A+y_I}{2}$

Proposition 2 : $x_I=\frac{x_A+x_B}{2}$ et $y_I=\frac{y_A+y_B}{2}$

b. Dans la bonne proposition trouvée précédemment, remplacer les lettres de la formule par des nombres , par $x$ et par $y$ .

c. Résoudre les équations suivantes:

\frac{-2+x}{2}=1

\frac{2+y}{2}=3

d. En déduire les coordonnées du point B.

Exercice n°4 :

Soient trois points $A(-2;3)$ , $B(1;2)$ et $C(0;-1)$ d’un repère orthonormé.

Calculer les trois distances $AB, AC, BC$ .

Avant de vous lancer dans les calculs, déterminer les trois distances à l’aide de Géogébra. Pour cela cliquer sur le 8ème onglet en haut en partant de la gauche, sélectionner Distance ou longueur dans le menu déroulant puis cliquer sur les deux points dans le repère. Les distances obtenues sont des valeurs approchées alors qu’avec le calcul on obtiendra des valeurs exactes.

2. Démontrer que le triangle $ABC$ est rectangle et isocèle en $B$ .

Exercice n°5 :

Soient deux points $A(4;0)$ , $B(2;2\sqrt{3})$ d’un repère orthonormé d’origine $O$ .

Calculer les trois distances $OA, OB, AB$ .

Avant de vous lancer dans les calculs, déterminer les trois distances à l’aide géogébra. Pour cela cliquer sur le 8ème onglet en haut en partant de la gauche, sélectionner Distance ou longueur dans le menu déroulant puis cliquer sur les deux points dans le repère.

2. En déduire la nature du triangle $OAB$ . Justifier.

Exercice n°6 :

Soient $A(-3;1)$ , $B(2;3)$ , $C(2;-1)$ et $D(-3;-3)$ quatre points d’un repère orthonormé.

On se propose de montrer que $ABCD$ est un parallélogramme de deux façons différentes.

Méthode 1 : On montre que les diagonales ont même milieu.

a. Calculer les coordonnées de $I$ , le milieu de $[AC]$ .

On peut conjecturer les coordonnées du milieu $I$ en utilisant la fenêtre géogébra ci-dessus. Pour cela on clique sur le deuxième onglet en partant de la gauche et on sélectionne Milieu ou centre dans le menu déroulant. Dans le repère on clique gauche sur le point A et sur le point C, le logiciel nomme le milieu E. Pour le renommer on clique droit sur E et on sélectionne Renommer dans le menu déroulant. On renomme le point avec la lettre I. On lit ses coordonnées dans la colonne Algèbre.

b. Calculer les coordonnées de $J$ , le milieu de $[BD]$ .

On peut conjecturer les coordonnées du milieu $J$ en utilisant la fenêtre géogébra ci-dessus. Pour cela on clique sur le deuxième onglet en partant de la gauche et on sélectionne Milieu ou centre dans le menu déroulant. Dans le repère on clique gauche sur le point B et sur le point D, le logiciel nomme le milieu E. Pour le renommer on clique droit sur E et on sélectionne Renommer dans le menu déroulant. On renomme le point avec la lettre J. On lit ses coordonnées dans la colonne Algèbre.

c. En déduire la nature du parallélogramme $ABCD$ . Justifier.

Méthode 2 : On montre que les côtés opposés ont même longueur deux à deux.

a. Calculer les distances $AB$ et $DC$ . Conclure.

Avant de vous lancer dans les calculs, déterminer les les distances à l’aide géogébra. Pour cela cliquer sur le 8ème onglet en haut en partant de la gauche, sélectionner Distance ou longueur dans le menu déroulant puis cliquer gauche sur les deux points dans le repère.

b. Calculer les distances $AD$ et $BC$ . Conclure.

c. En déduire la nature du parallélogramme $ABCD$ . Justifier.

Exercice n°7 :

Soient $A(4;-1)$ , $B(7;3)$ , $C(2;3)$ et $D(-1;-1)$ quatre points d’un repère orthonormé.

On se propose de démontrer que le quadrilatère $ABCD$ est un losange.

Méthode 1 : On montre que les diagonales ont même milieu et qu’elles sont perpendiculaires.

1.a. Déterminer par le calcul , les coordonnées de $I$ le milieu de $[AC]$ .

1.b. Déterminer par le calcul , les coordonnées de $J$ le milieu de $[BD]$ .

1.c. En déduire que les diagonales $[AC]$ et $[BD]$ ont même milieu.

2.a. Calculer les distances $BI$ , $IC$ et $BC$ .

2.b. Comparer $BI^2+IC^2$ et $BC^2$ .

2.c. En déduire que le triangle $BIC$ est rectangle en $I$ .

3. En déduire que le quadrilatère $ABCD$ est un losange.

Méthode 2 : On montre que les quatre côtés ont même longueur.

1) Calculer les distances $AB, CD$ et $AD$ .

2. En déduire que le quadrilatère $ABCD$ est un losange.