Sommaire
Variables
En programmation une variable peut être comparée à une boîte ou une case à laquelle on a donné un nom. Elle contient la dernière valeur rentrée c’est-à-dire que toute nouvelle valeur rentrée chasse la précédente.
Il existe différents types de variables :
- entier
- flottant (nombre à virgule)
- chaîne de caractères (suite ordonnée de caractères)
- booléen ( variable qui ne prend que deux valeurs vrai ou faux)
Affectation
Les instructions d’entrée-sortie
En matière d’entrée avec le langage Python, on peut écrire:
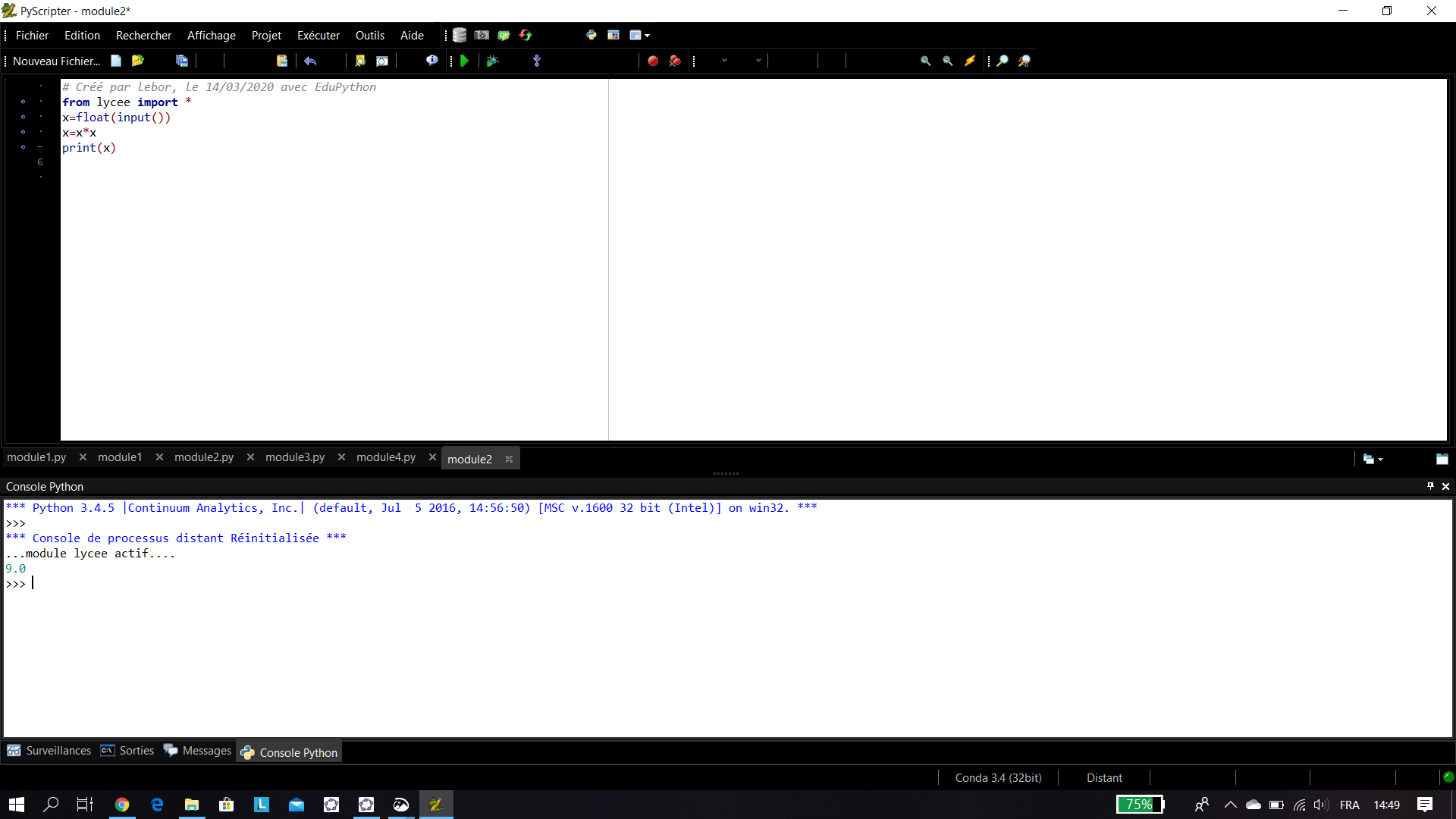
- t=float(input()) (voir paragraphe 3 exemple n°1)
- a=demande() (voir Exemple n°3 paragraphe 5 )
- a=0 (voir Exemple n°1 paragraphe 4 )
- Dans le cas d’une fonction comme l’ exemple 1 du paragraphe 3 : Dans la console on tape , par exemple det(1,1,3,3)
Exemple n°1:
Instructions conditionnelles
Dans un programme on peut être amené à tester une condition et à excécuter telle ou telle instruction suivant que la condition est vérifiée ou non.
En matière d’instruction conditionnelle avec le langage Python, on peut écrire:
if d==0 :
print (« les vecteurs sont colinéaires »)
else :
print (« les vecteurs ne sont pas colinéaires »)
Remarque : toujours finir les lignes if (condition) et else par : (deux points)
Puis écrire l’instruction sur la ligne suivante ( cette ligne est décalée sur la droite par rapport à la précédente)
Pour s’en rappeler : deux points à la ligne.
Exemple 1 : Voici un programme pour tester la colinéarité de deux vecteurs.
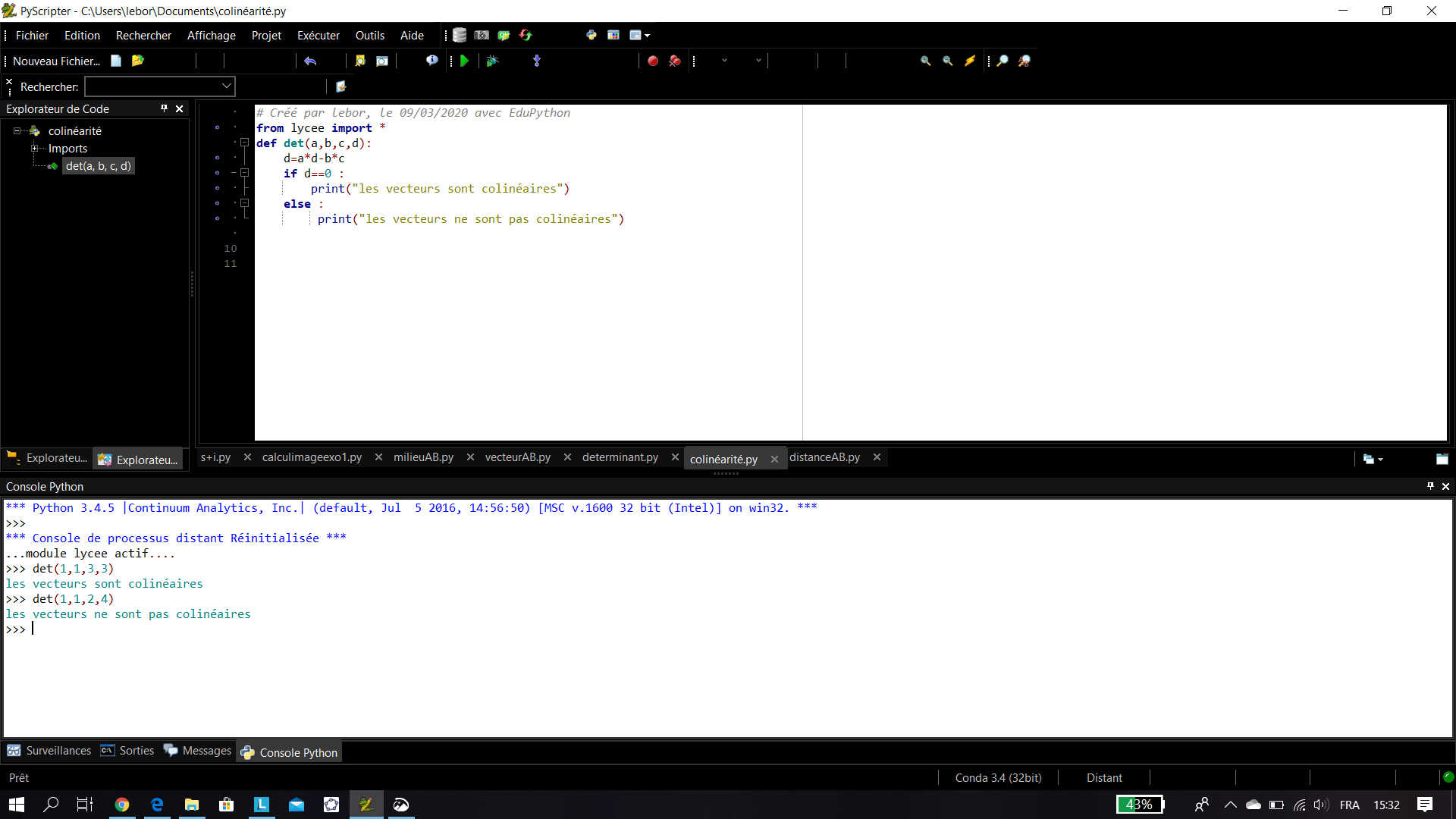
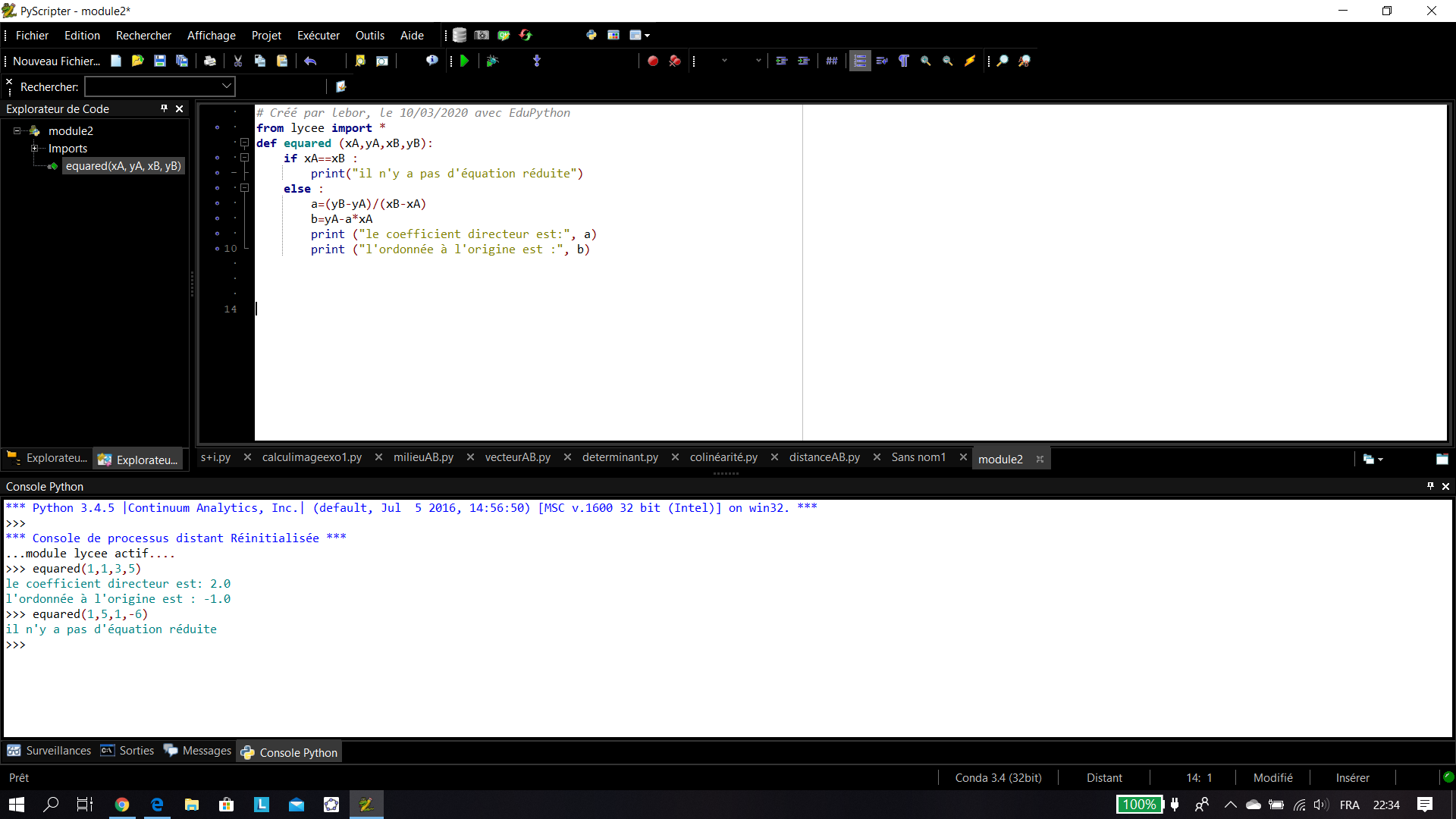
Exemple n°2 : Voici un programme pour déterminer quand c’est possible l’équation réduite d’une droite.
Boucles bornées
La boucle bornée pour i allant de 1 à n permet d’exécuter n fois un même bloc d’instructions.
En matière de boucles bornées avec le langage Python, on peut écrire ( on n’oublie pas les deux points à la ligne )
for i in range(1,11) :
(instruction)
Remarque: i prendra les valeurs de 1 à 10 ( celles qui sont strictement inférieures à 11).
En réalité, il faudrait rajouter une troisième valeur : le pas.
Quand on écrit for i in range(1,11) : cela correspond à for i in range(1,11,1) : c’est-à-dire qu’on compte de 1 en 1 , les valeurs prises par i sont 1, 2, 3, 4…, 10.
Si on écrit for i in range(1,11,2) : , on compte de 2 en 2 , les valeurs prises par i sont 1, 3, 5, 7, 9.
Enfin si on on écrit for i in range(3) , les valeurs prises par i sont 0, 1 et 2.
Exemple n°1: Voici un programme qui permet de calculer les dix pemiers nombres triangulaires.,
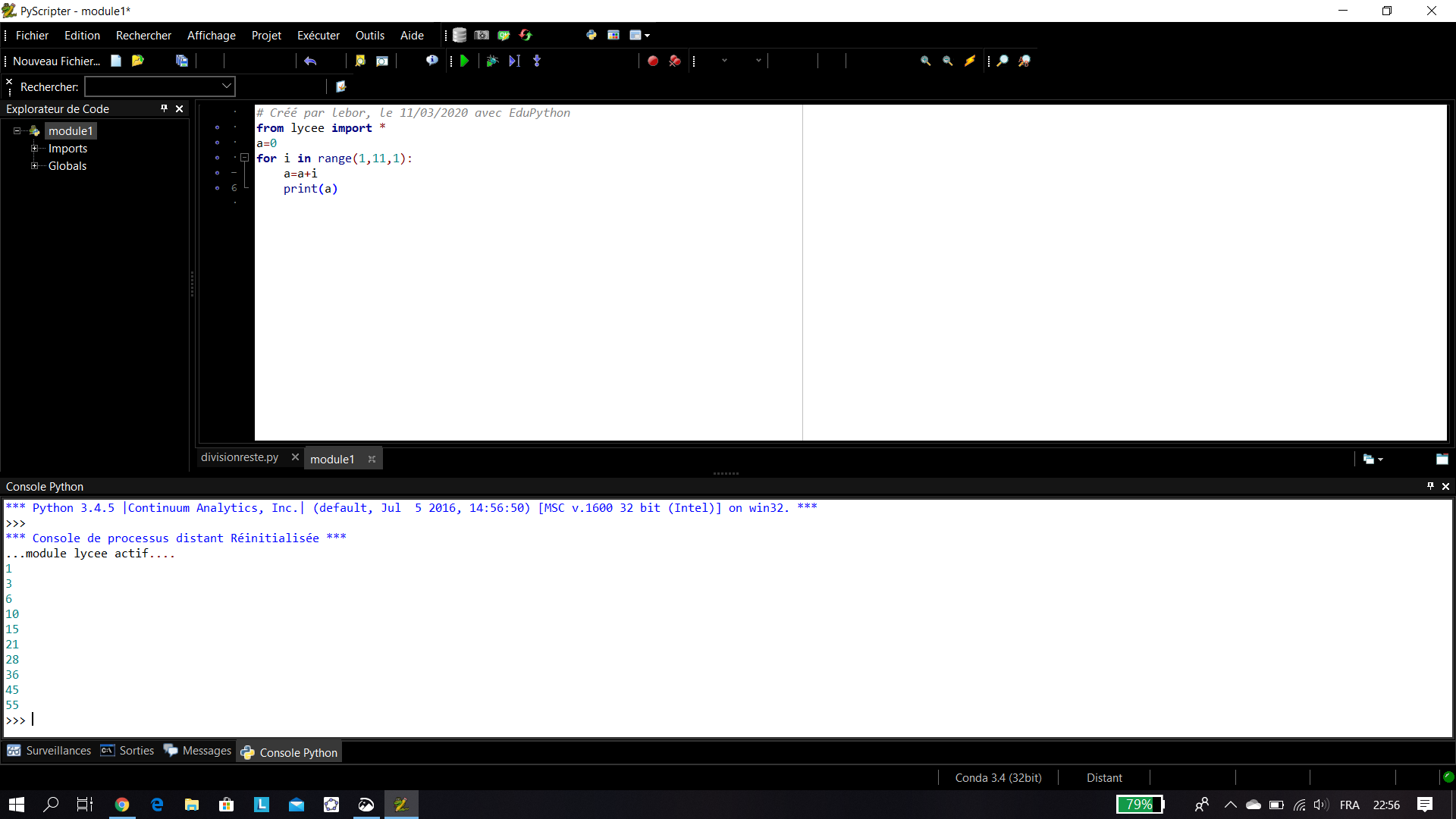
Boucles non bornées
La boucle non bornée tant que… permet d’excécuter un même bloc d’instructions tant qu’une condition reste vraie.
En matière de boucles non bornées avec le langage Python, on peut écrire ( on n’oublie pas les deux points à la ligne ) comme dans l’exemple n°1 paragraphe 5
while a>=7 :
(instruction)
Exemple n°1: déterminer le reste dans la division d’un nombre donné par 7.
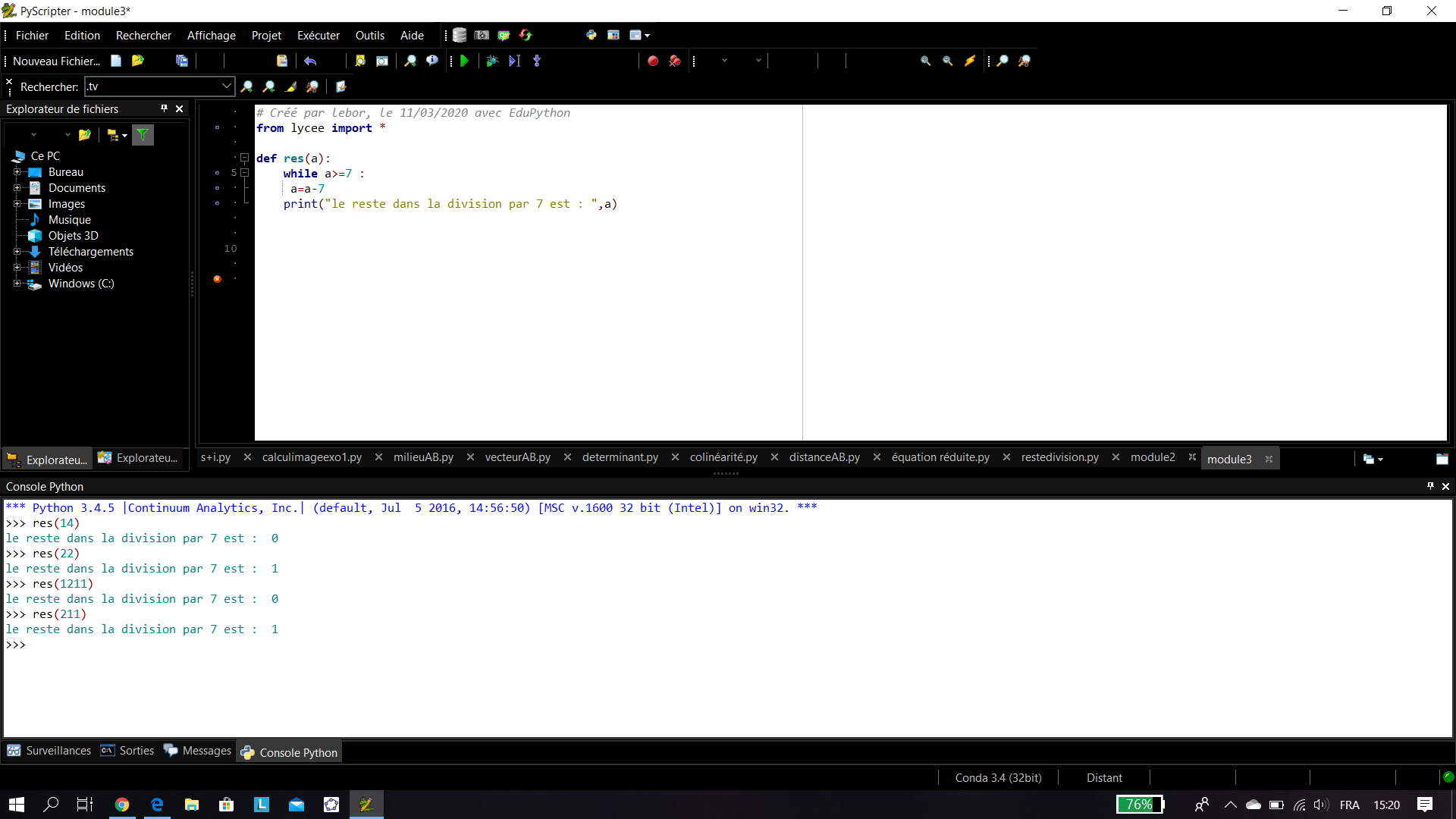
Exemple n°2: Evolution de la vente des téléphones portables en France. En 2009, il s’est vendu 3 millions de portables en France. Avec un taux d’augmentation de 40% d’une année sur l’autre, en quelle année aura-t-on vendu plus de 20 millions d’unités ?
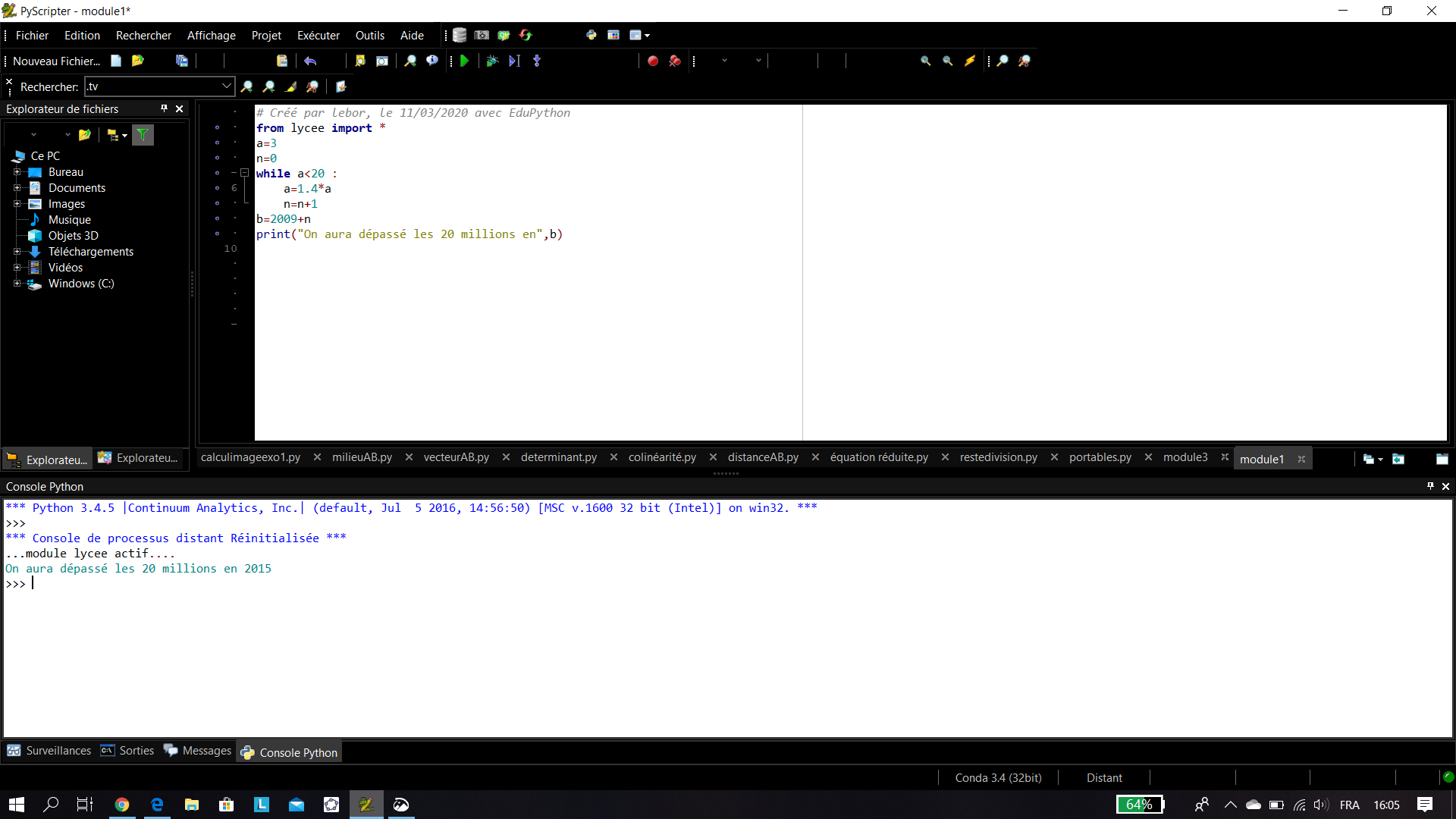
Exemple n°3: déterminer le reste dans la division d’un nombre donné a par un nombre donné b.
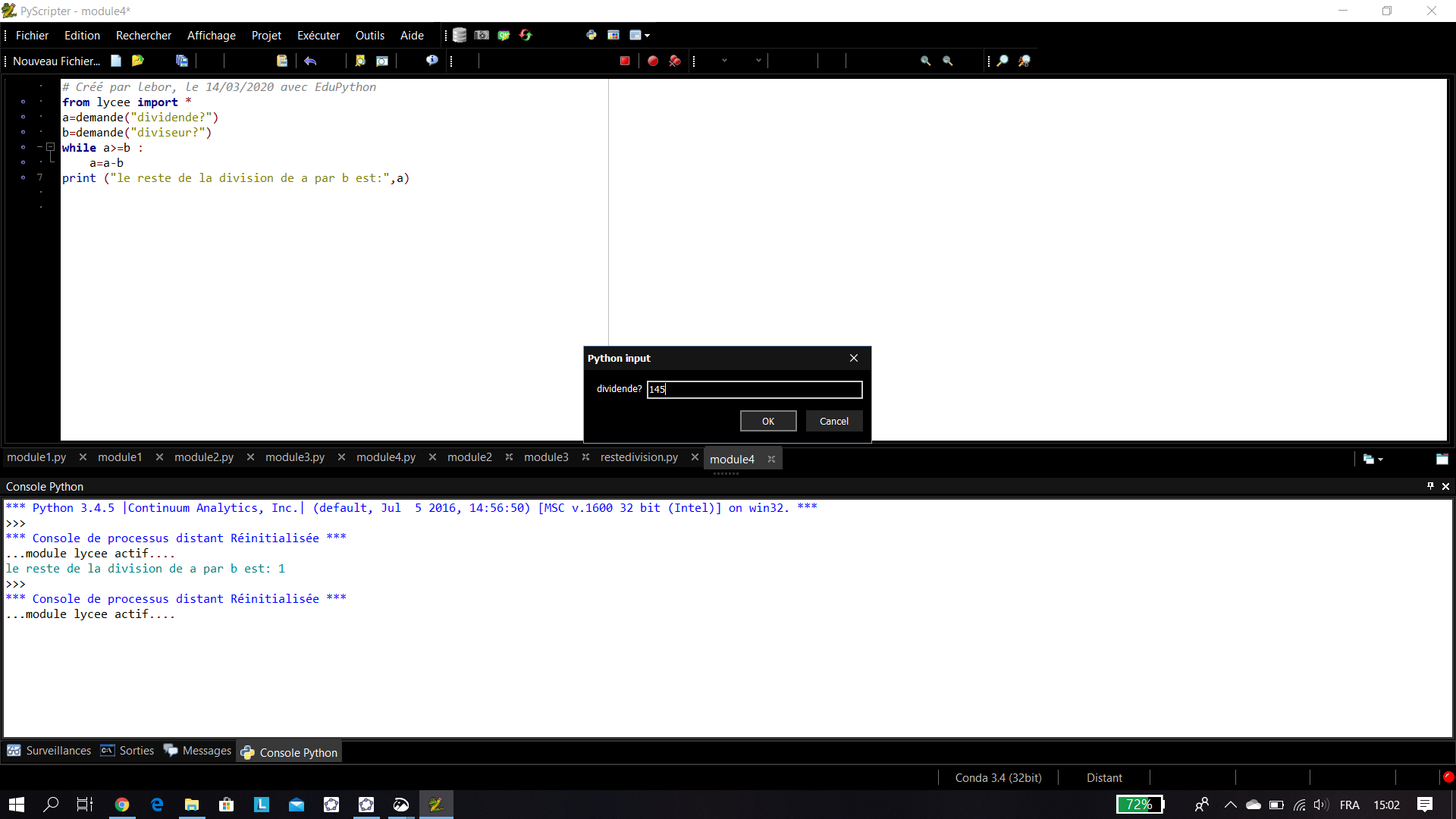
Fonctions
On peut définir des fonctions en programmation. Elles possèdent des paramètres et un bloc d’instructions, elles renvoient un résultat et peuvent être appelées plusieurs fois par un programme.
En matière de fonctions avec le langage Python, on peut écrire ( on n’oublie pas les deux points à la ligne ) comme dans l’exemple n°1 paragraphe 6
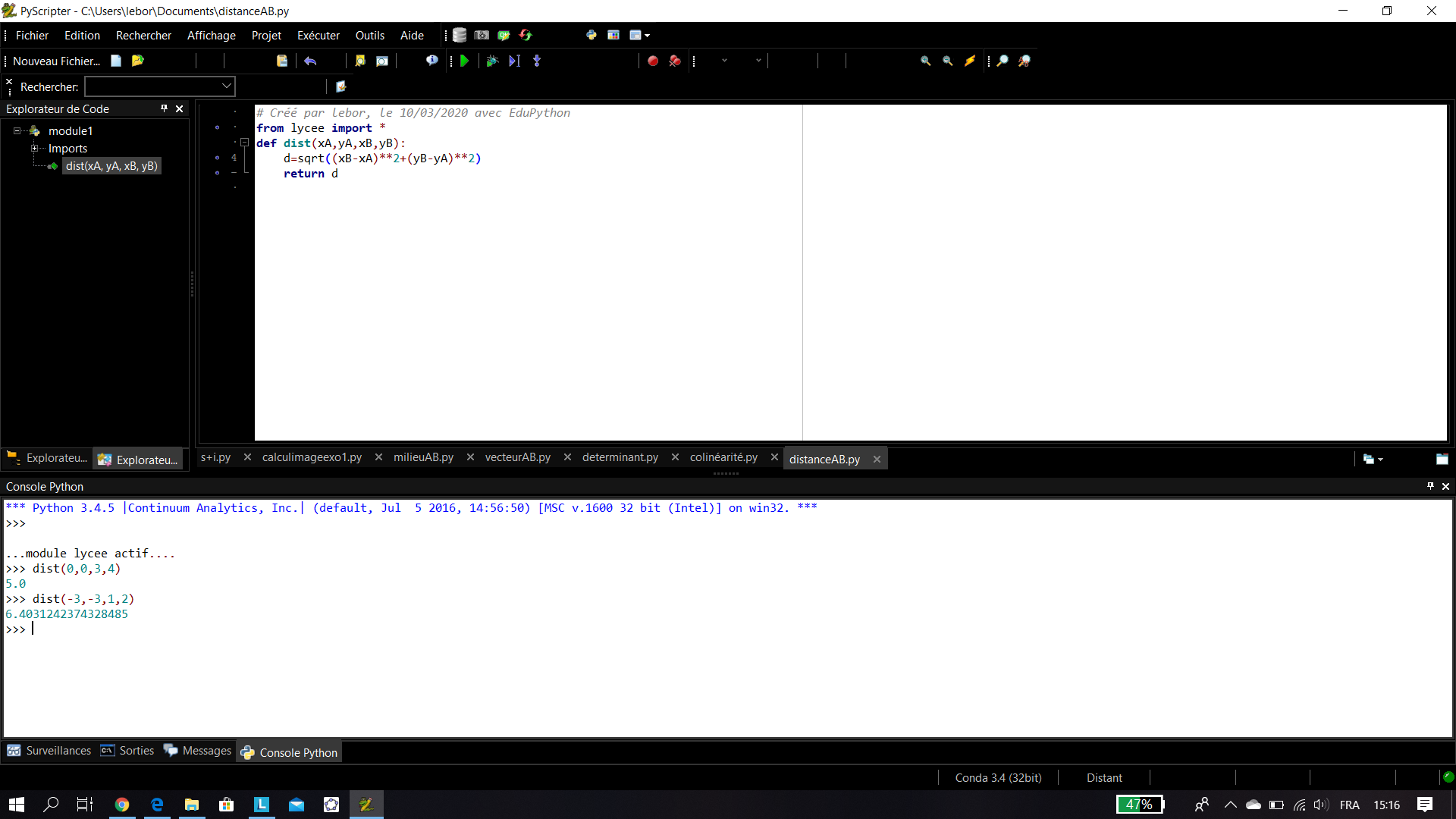
def dist(xA,yA,xB,yB) :
(bloc d’instructions)
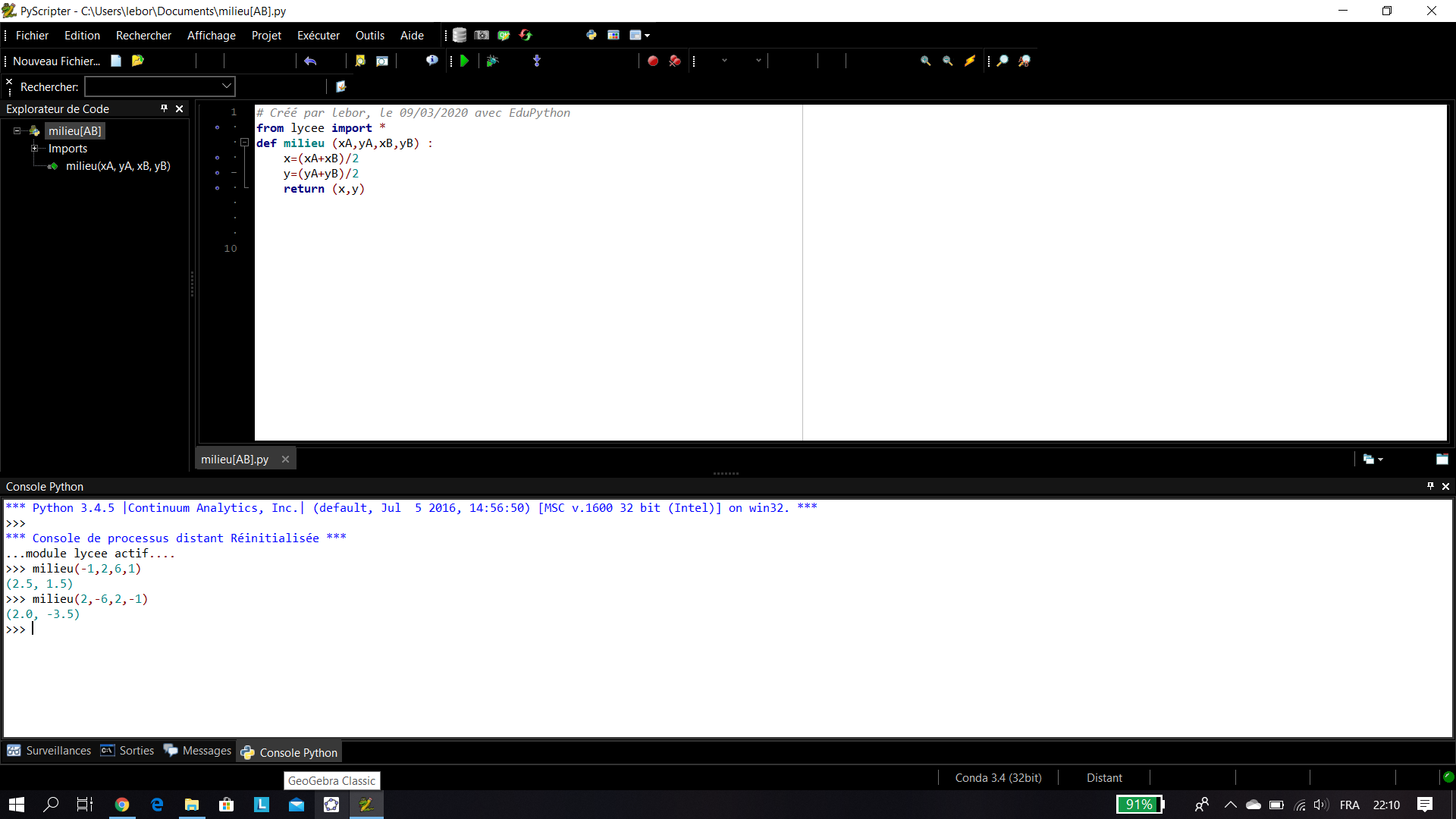
Exemple n°1: Voici une fonction qu’on a baptisée dist qui calcule la distance entre deux points A et B.
Exemple n°2: Voici une fonction qu’on a baptisée milieu qui calcule les coordonnées du milieu de deux points A et B.