2.Arithmétique.

Définition n°1 : Soient $a$ et $b$ deux nombres entiers relatifs.

$a$ est un diviseur de $b$ s’il existe $k\in\mathbb{Z}$ tel que $b=k\times a$ .

On dit aussi que $b$ est un multiple de $a$ .

Propriété n°1:

Soit $a\in\mathbb{Z}$ , la somme de deux multiples de $a$ est un multiple de $a$ .

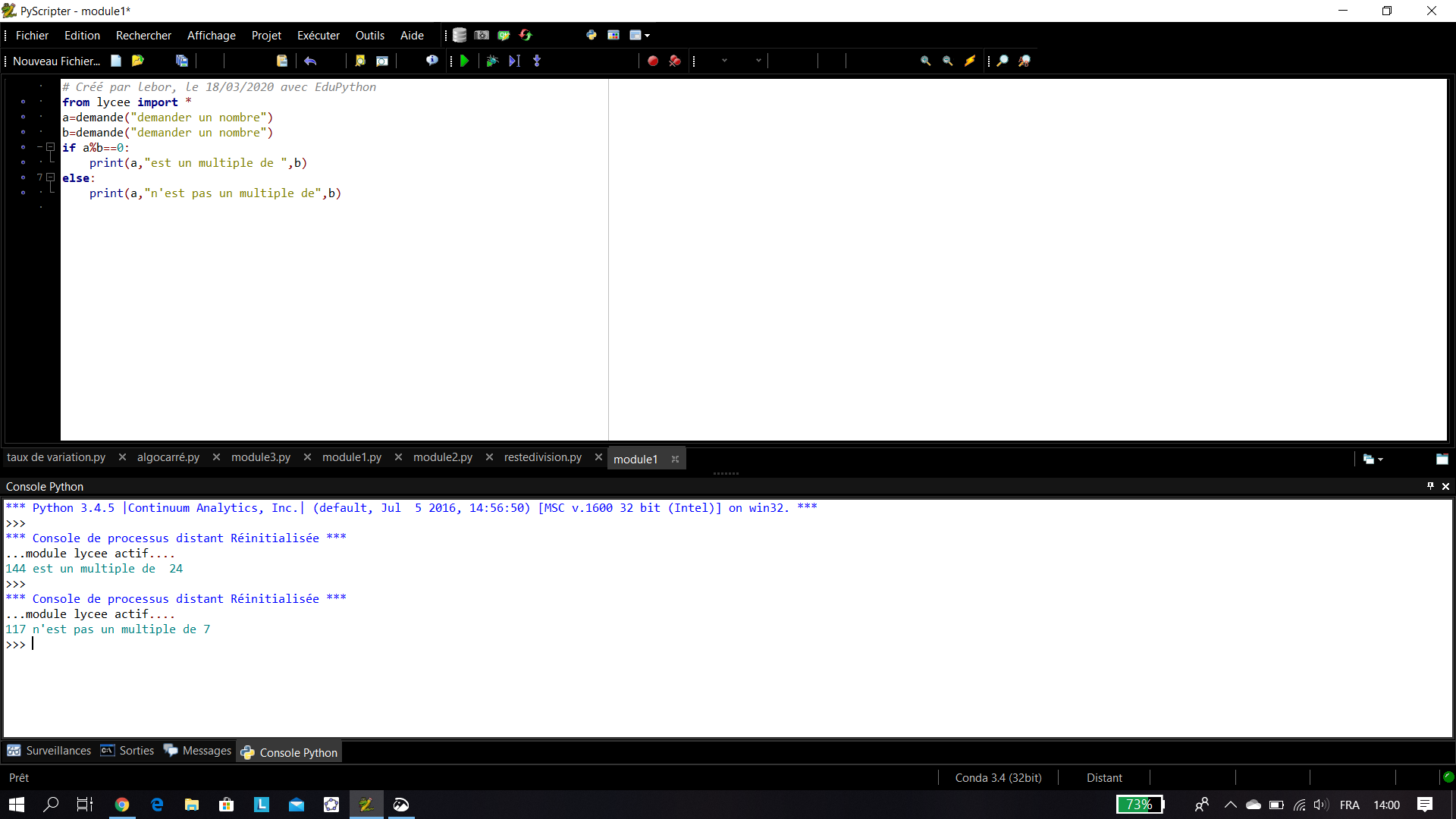
Algorithme 1: Déterminer si un entier naturel $a$ est multiple d’un entier naturel $n$ .

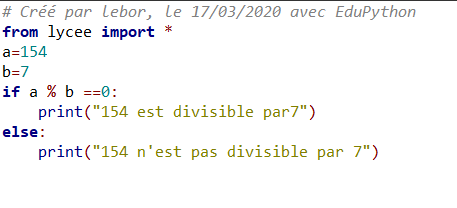
Exemple n°1: 154 est-il un multiple de 7 ?

1) Répondre en utilisant la définition 1.

2) Répondre en utilisant un algorithme écrit en langage Python.

Algorithme 2: Pour des entiers $a$ et $b$ donnés, déterminer le plus grand multiple de $a$ inférieur ou égal à $b$ .

Définition n°2: Soit $a\in\mathbb{Z}\\a$ est pair s’il est divisible par 2 c’est-à-dire $a=2\times k$ .

$a$ est impair s’il n’est pas divisible par 2 c’est-à-dire $a=2\times k+1$ .

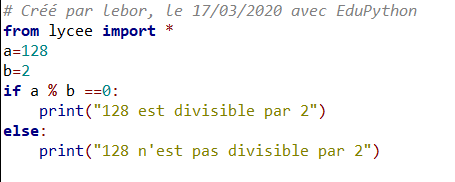
Exemple n°2: 128 est-il pair ?

2) Répondre en utilisant un algorithme écrit en langage Python.

Propriété n°2:

Le carré d’un nombre impair est impair.

Définition n°3: Un nombre premier est un nombre entier naturel qui a exactement deux diviseurs 1 et lui-même.

Exemple n°3 : En utilisant la définition n°3 montrer que tout nombre pair autre que 2 ne peut pas être premier.

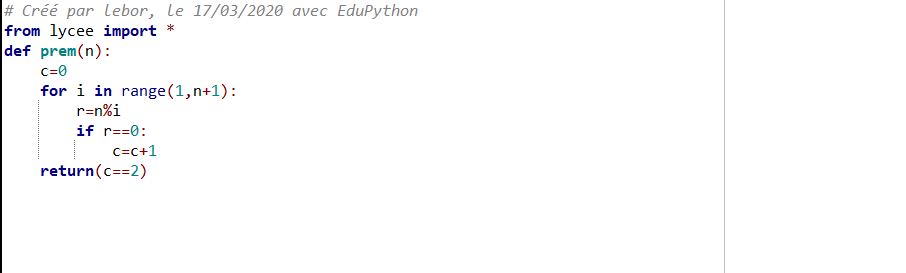
Algorithme 3 : Ecrire un algorithme en Python qui détermine si un entier naturel est premier.