Sommaire
Exercice n°1
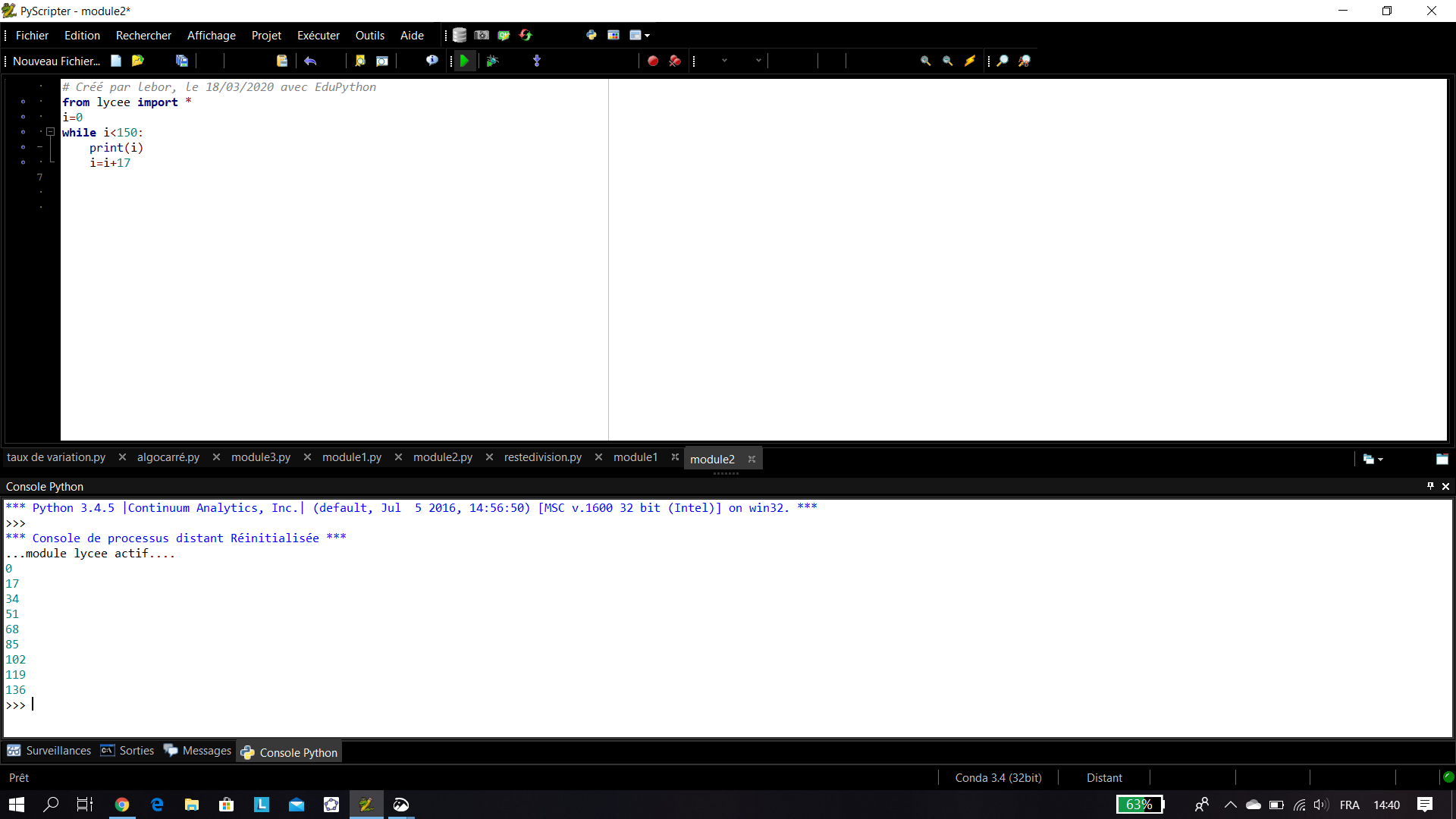
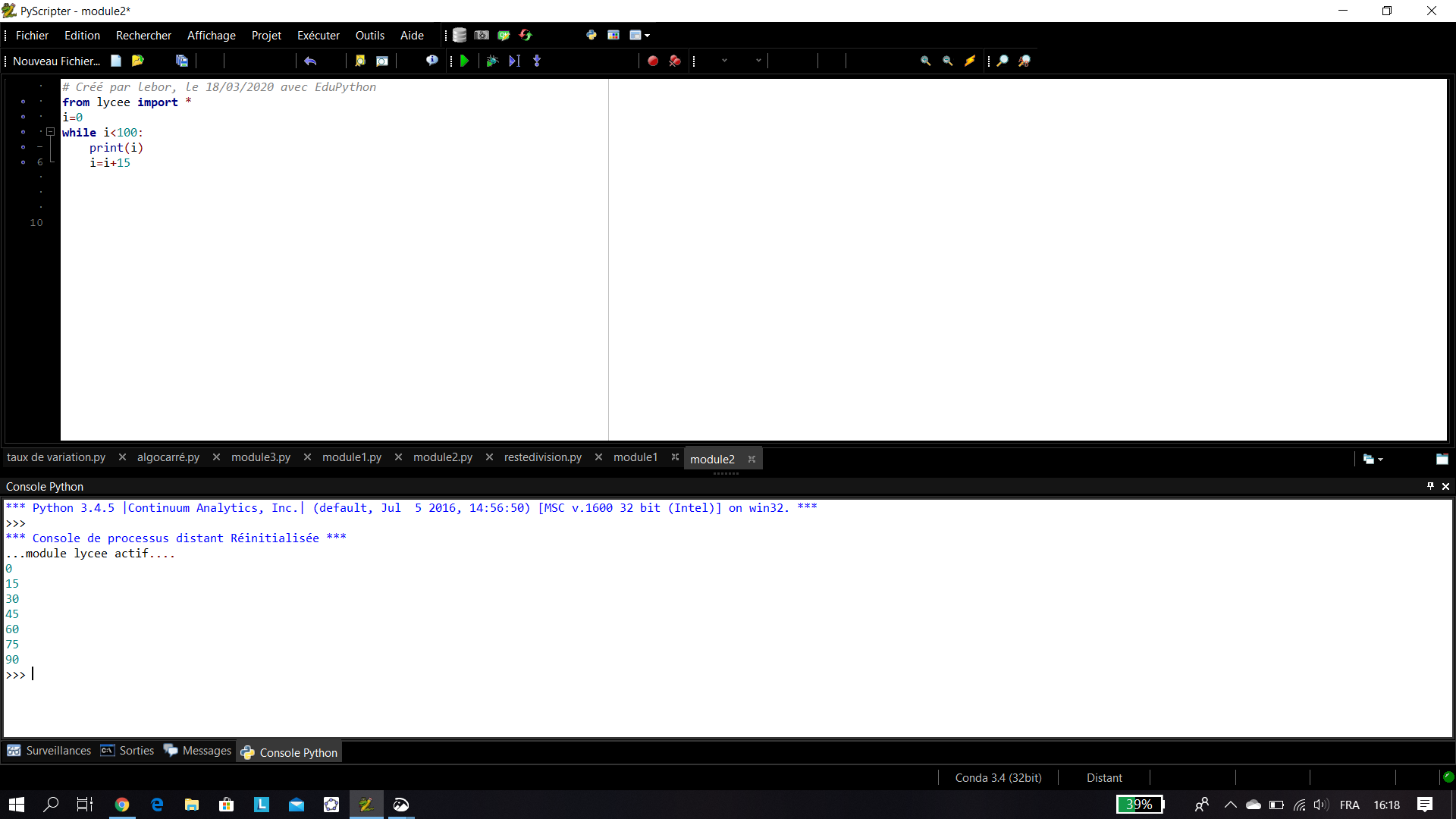
Déterminer tous les entiers naturels multiples de 17 inférieurs à150.
- En utilisant la définition 1 du cours.
2. En utilisant un algorithme écrit en langage Python.
Exercice n°2
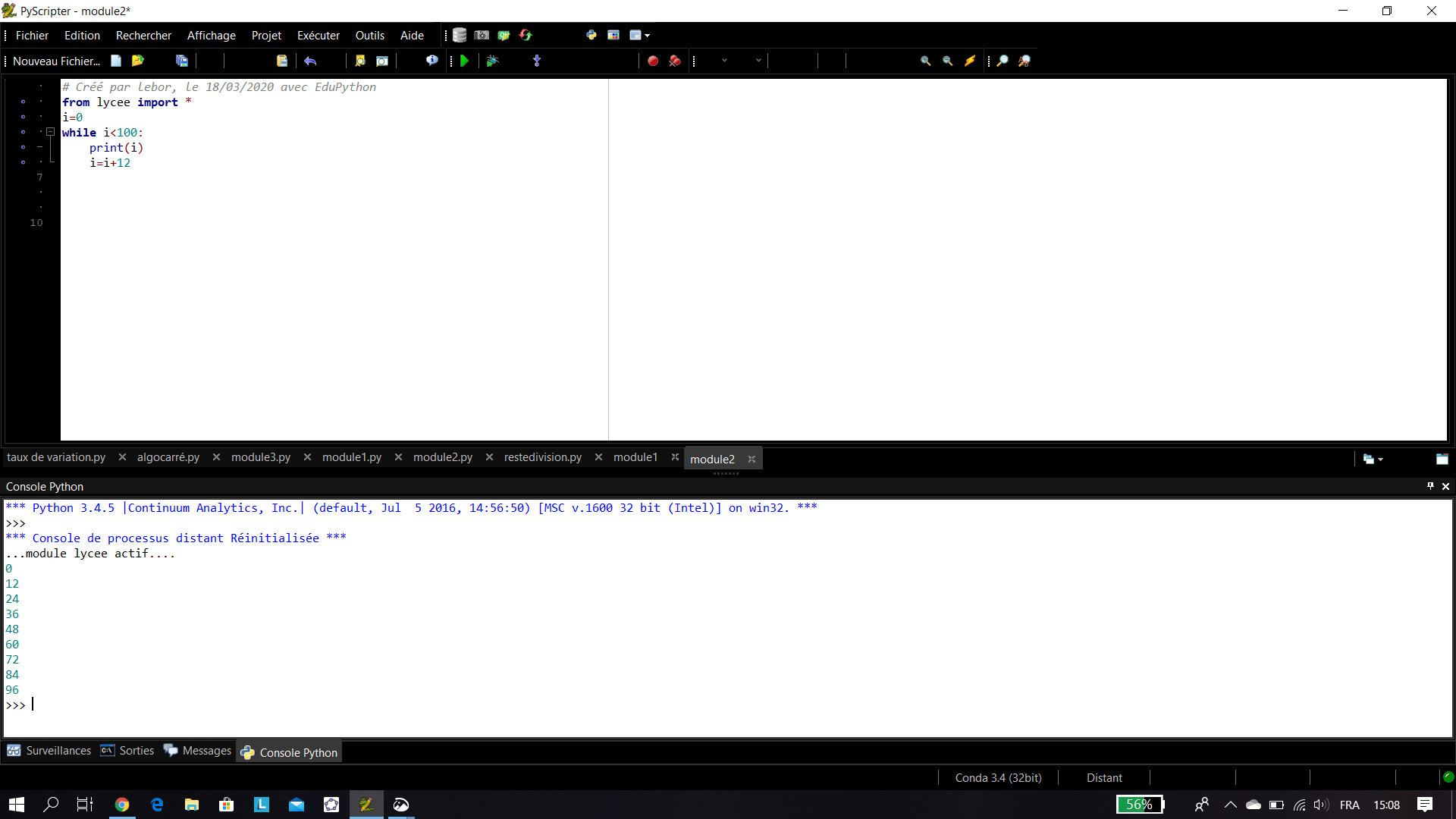
- Déterminer tous les entiers naturels multiples de 12 inférieurs à 100.
a. En utilisant la définition 1 du cours.
b. En utilisant un algorithme écrit en langage Python.
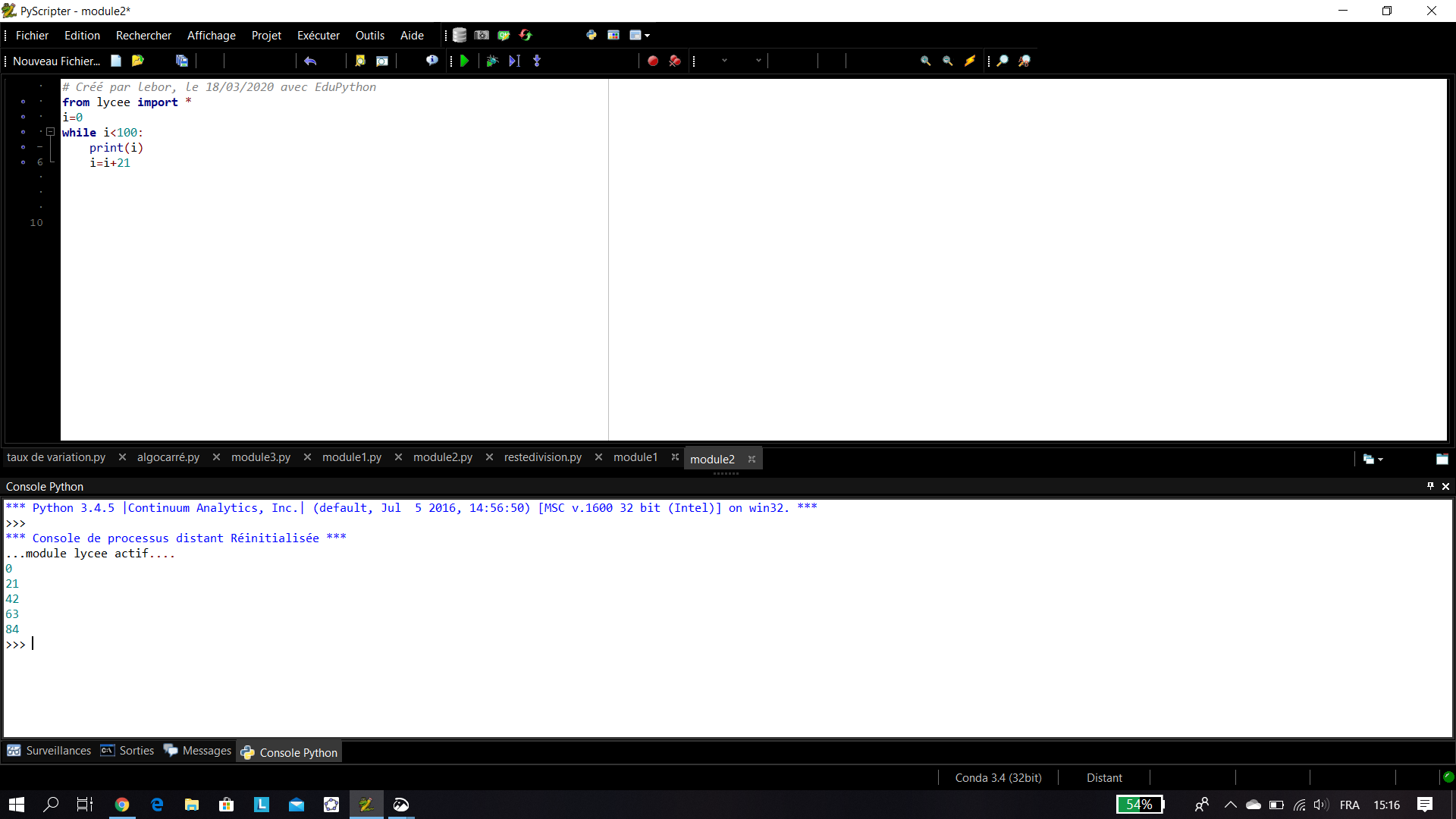
2. Déterminer tous les entiers naturels multiples de 21 inférieurs à 100.
a. En utilisant la définition 1 du cours.
b. En utilisant un algorithme écrit en langage Python.
3. Quel est le plus petit multiple commun non nul à 12 et à 21.
4. A l’aide de la question 3, calculer \frac{1}{12}+\frac{5}{21}
Exercice n°3
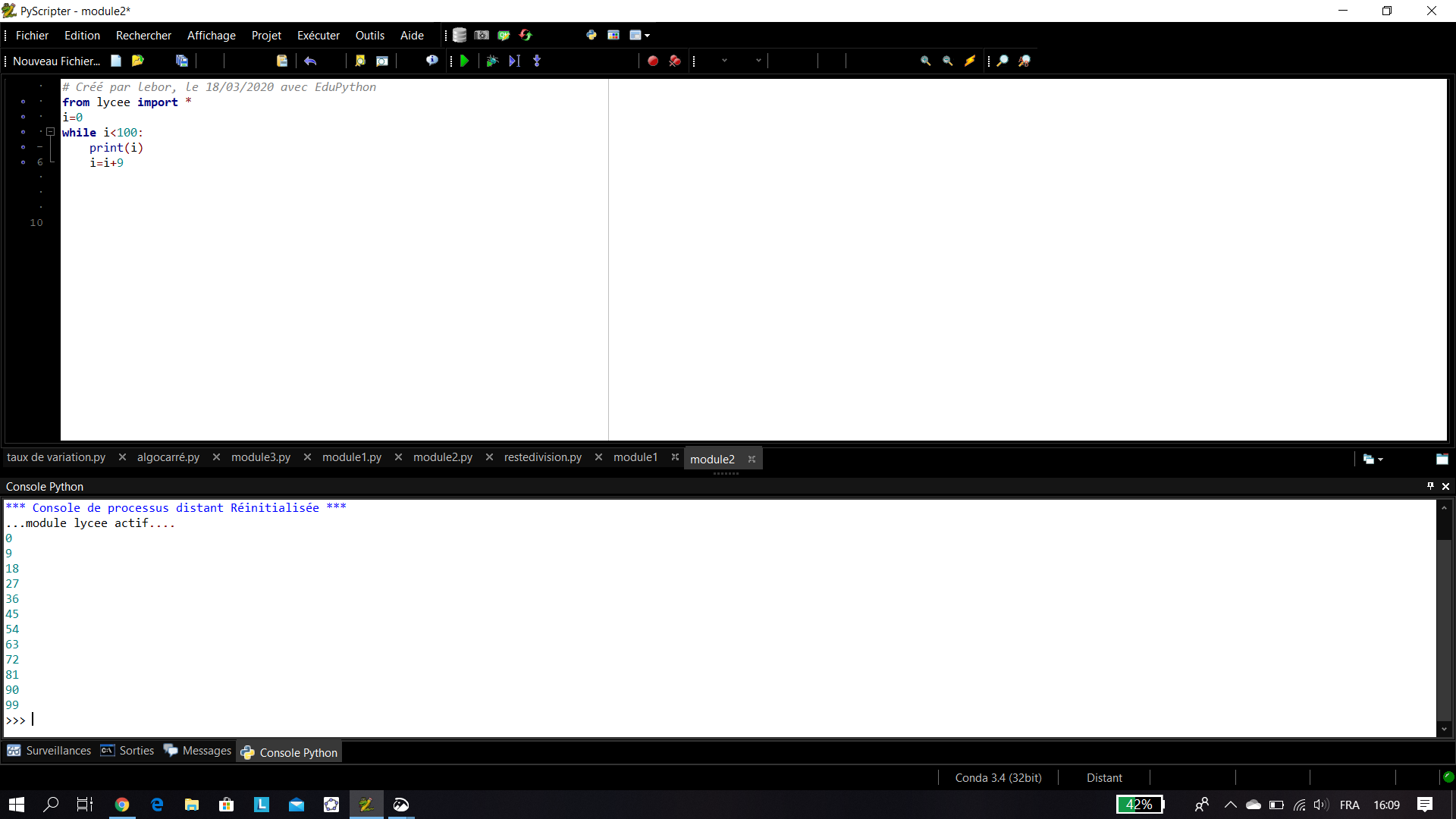
- Déterminer tous les entiers naturels multiples de 9 inférieurs à 100.
a. En utilisant la définition 1 du cours.
b. En utilisant un algorithme écrit en langage Python.
2. Déterminer tous les entiers naturels multiples de 15 inférieurs à 100.
a. En utilisant la définition 1 du cours.
b. En utilisant un algorithme écrit en langage Python.
3. Quel est le plus petit multiple commun non nul à 9 et à 15.
4. A l’aide de la question 3, calculer \frac{4}{9}-\frac{2}{15}
Exercice n°4
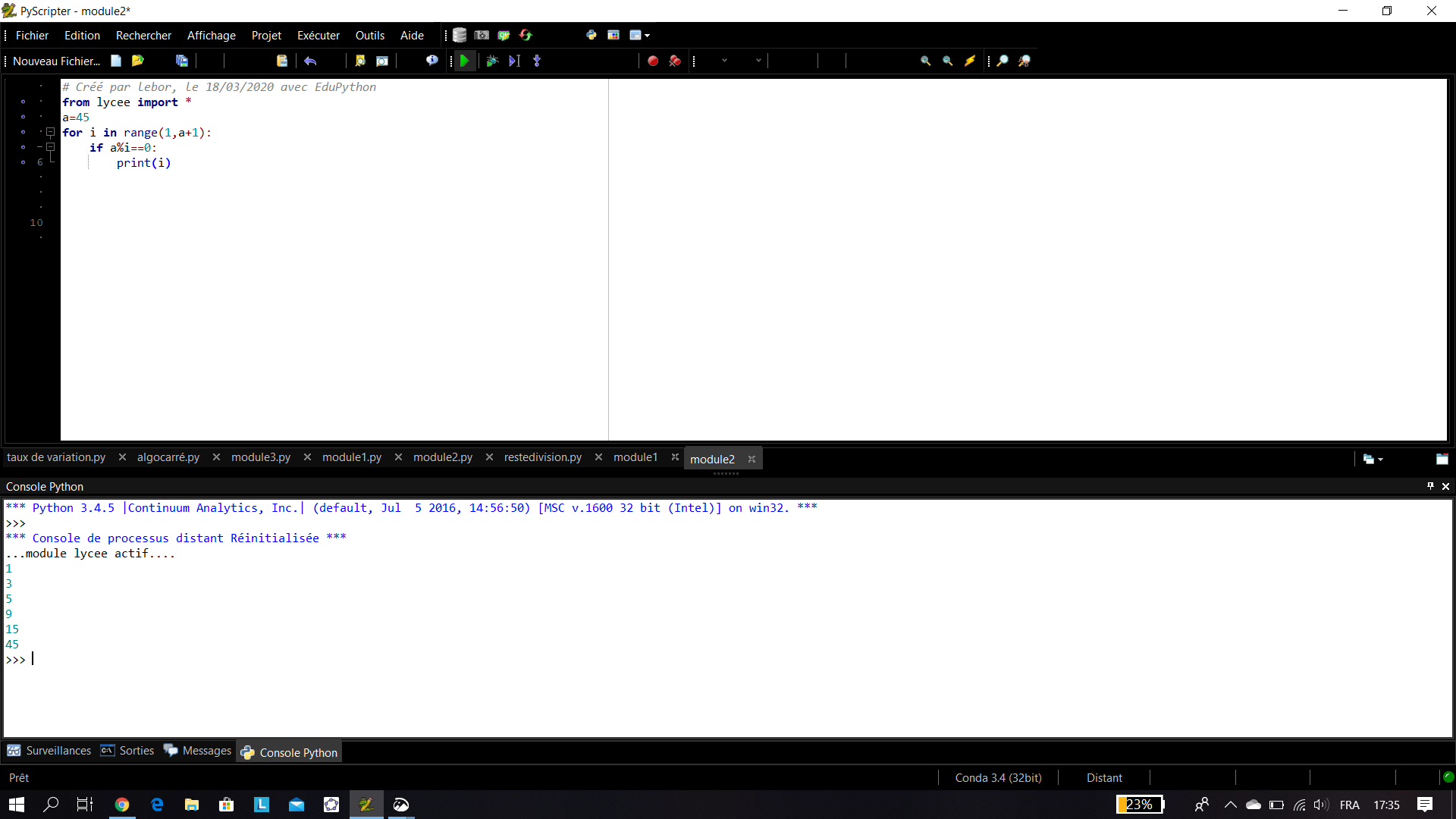
Déterminer tous les diviseurs positifs de 45.
1. En utilisant la définition 1 du cours.
2. En utilisant un algorithme écrit en langage Python.
Exercice n°5
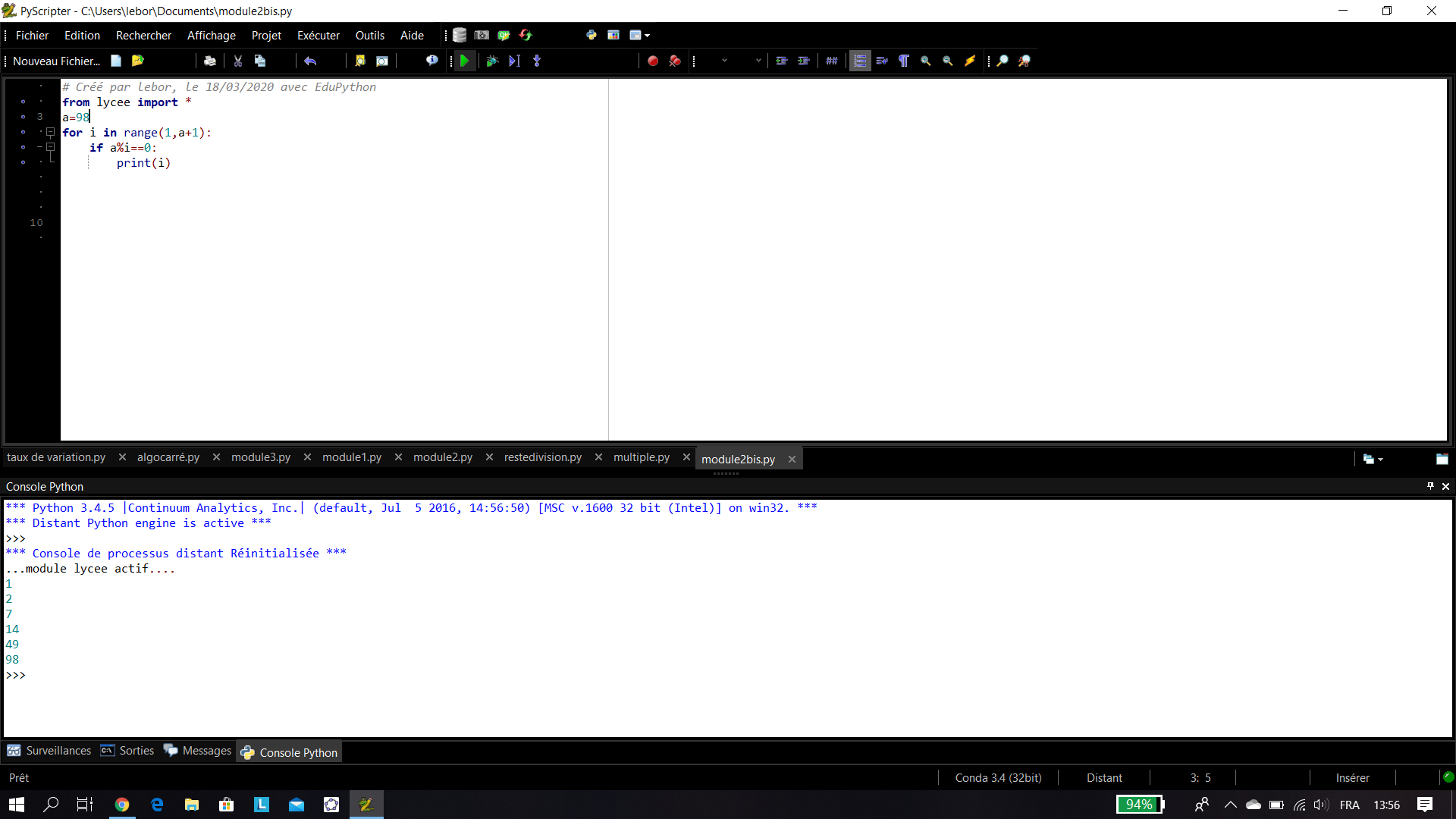
- Déterminer tous les diviseurs positifs de 98.
a. En utilisant la définition 1 du cours.
b. En utilisant un algorithme écrit en langage Python.
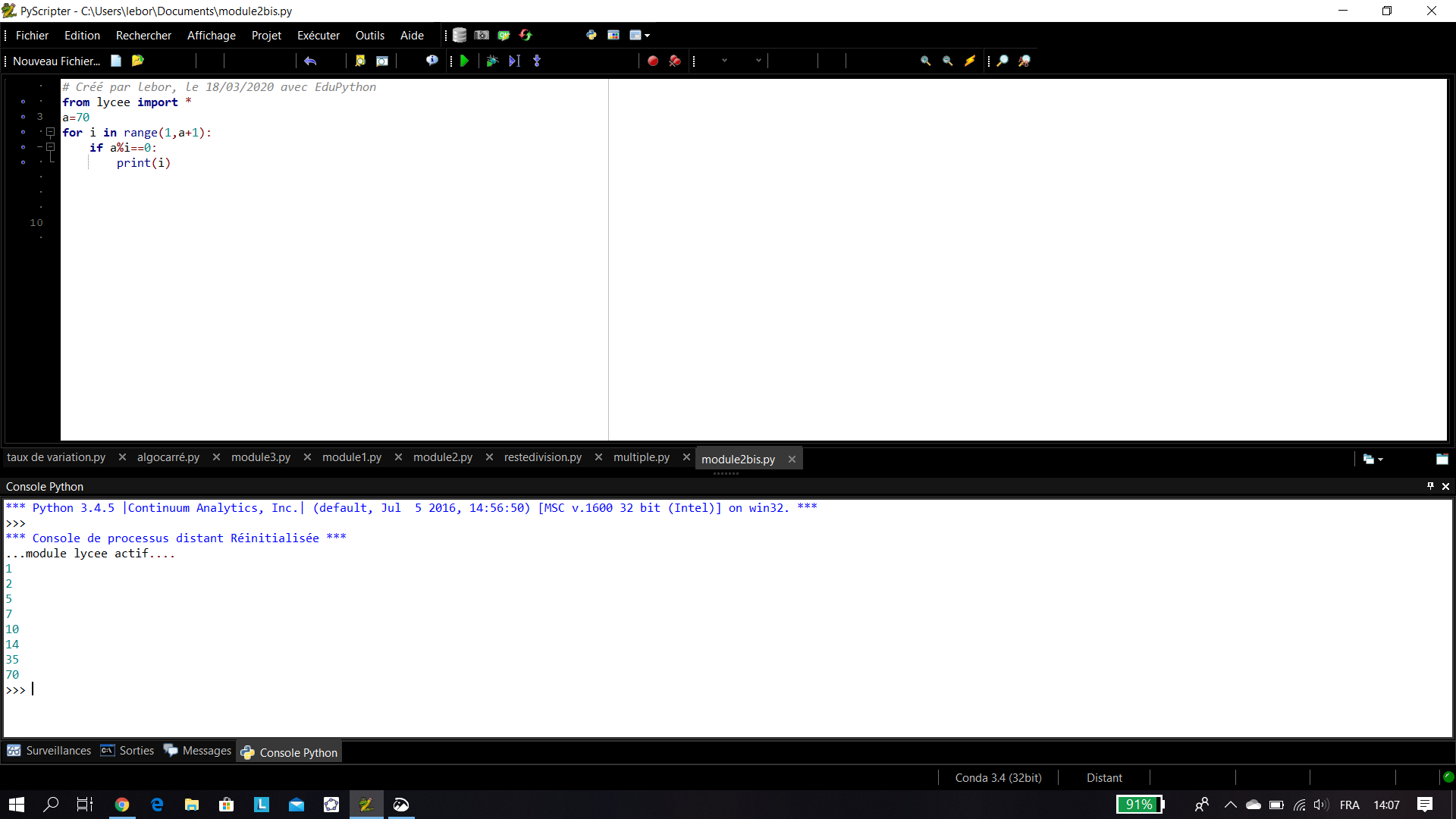
2. Déterminer tous les diviseurs positifs de 70.
a. En utilisant la définition 1 du cours.
b. En utilisant un algorithme écrit en langage Python.
3. Déterminer le plus grand diviseur commun à 98 et 70.
4. En utilisant le résultat de la question précédente écrire la fraction \frac{98}{70} sous forme irréductible.
Exercice n°6
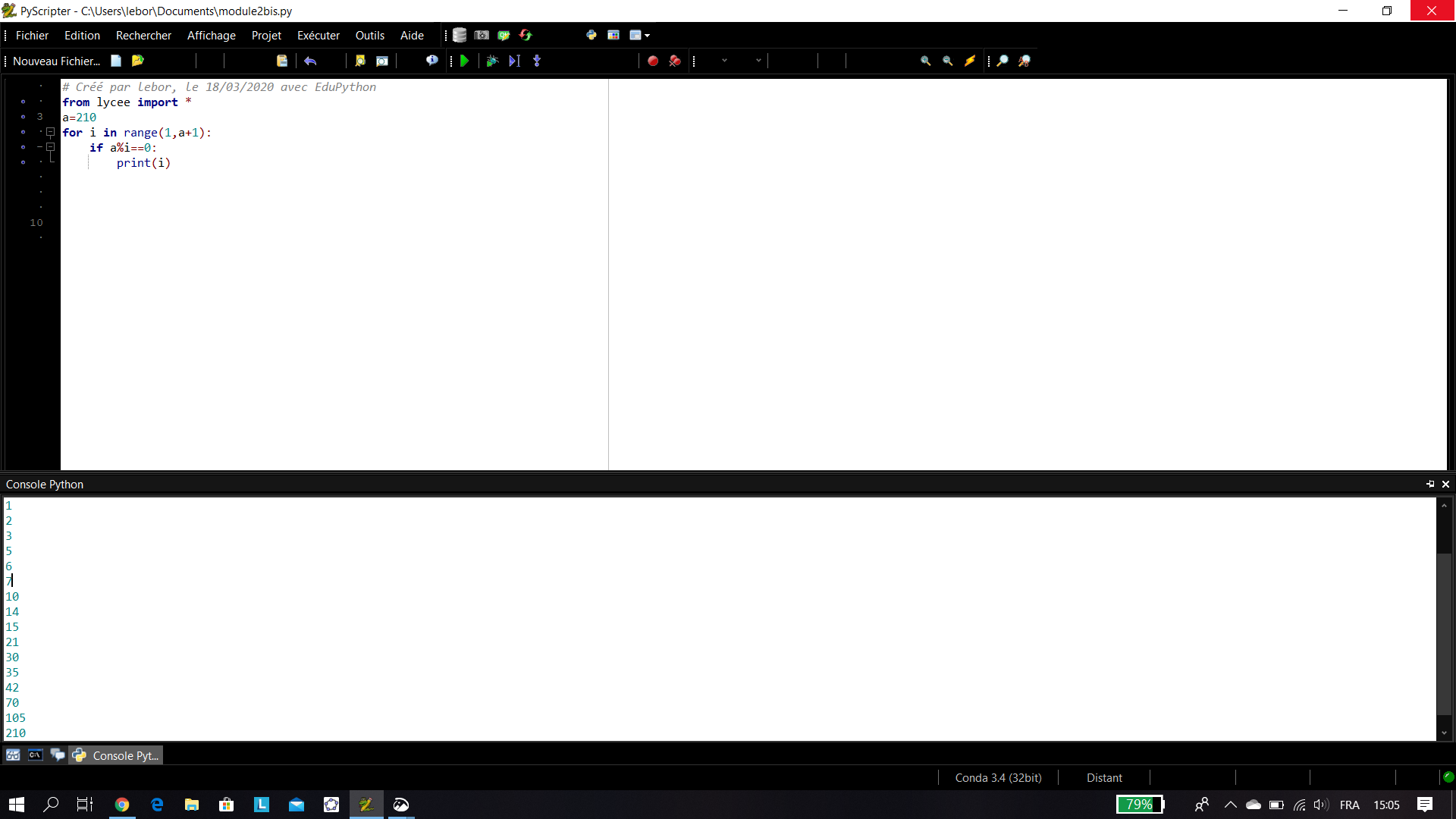
- Déterminer tous les diviseurs positifs de 210.
a. En utilisant la définition 1 du cours.
b. En utilisant un algorithme écrit en langage Python.
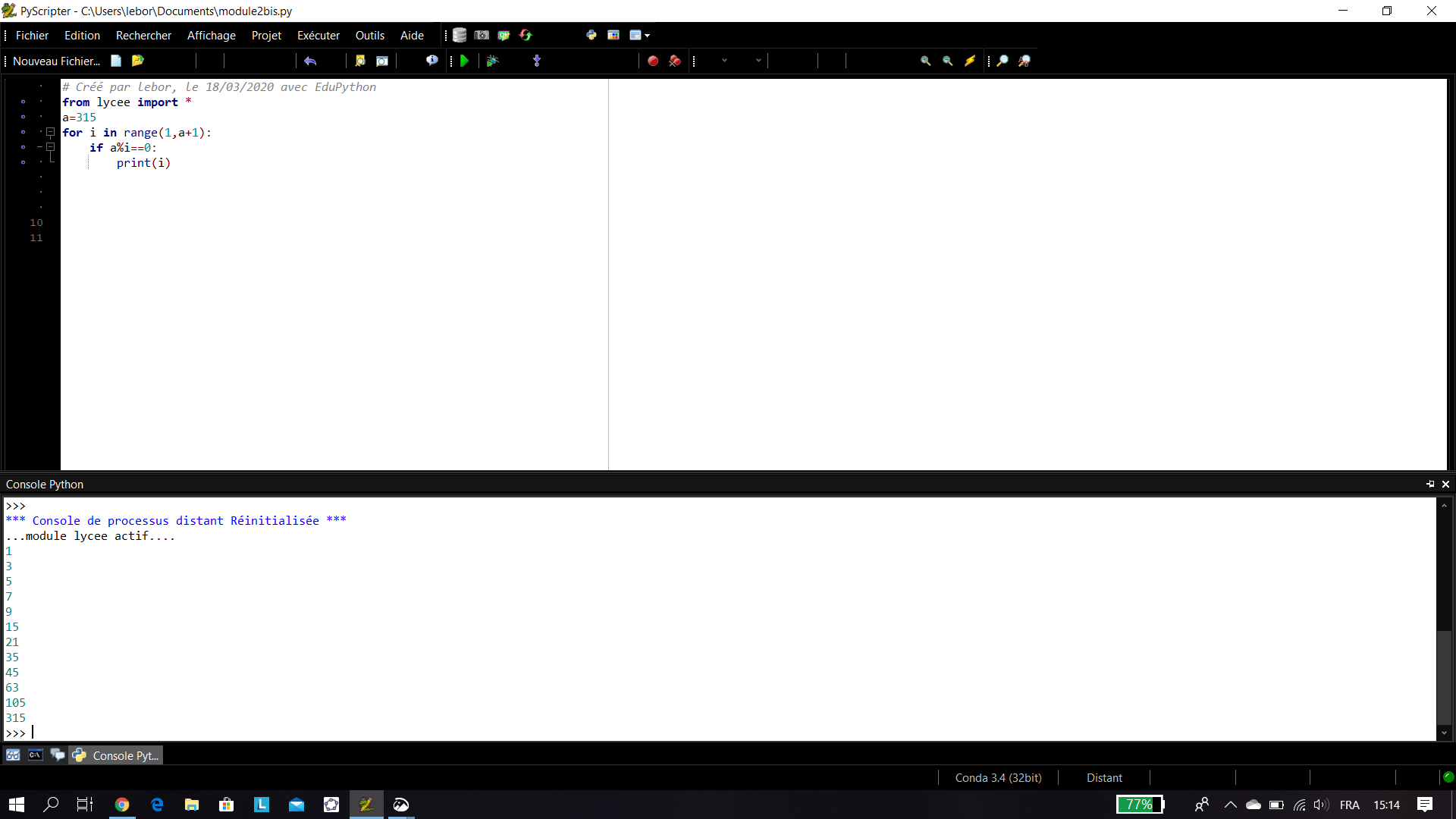
2. Déterminer tous les diviseurs positifs de 315.
a. En utilisant la définition 1 du cours.
b. En utilisant un algorithme écrit en langage Python.
3. Déterminer le plus grand diviseur commun à 98 et 70.
4. En utilisant le résultat de la question précédente écrire la fraction \frac{210}{315} sous forme irréductible.
Exercice n°7
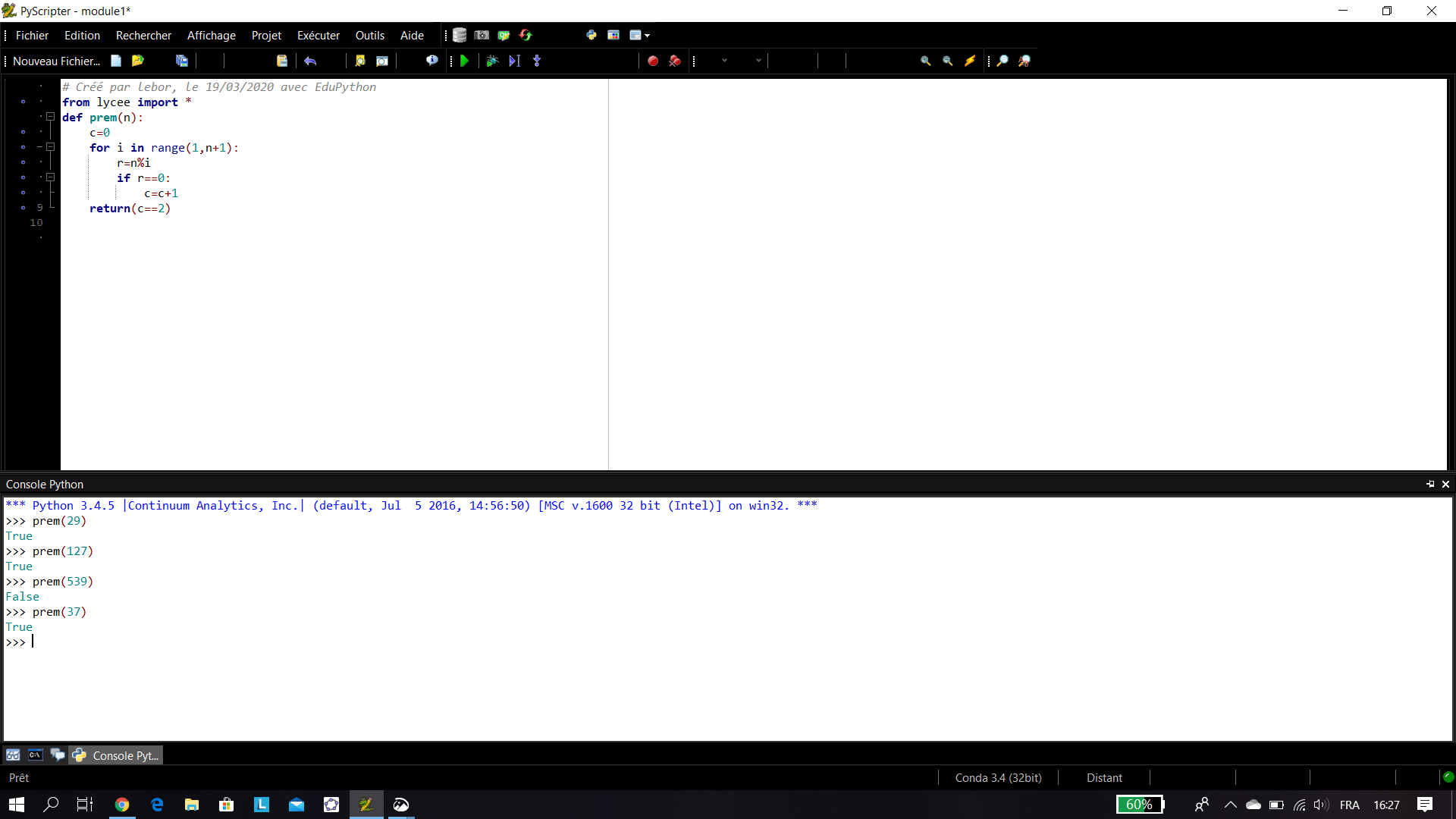
Les nombres suivants sont-ils premiers ? On pourra au besoin utiliser un algorithme écrit en langage Python.
21 25 29 34 37 120 127 306 335 372 539
Exercice n°8
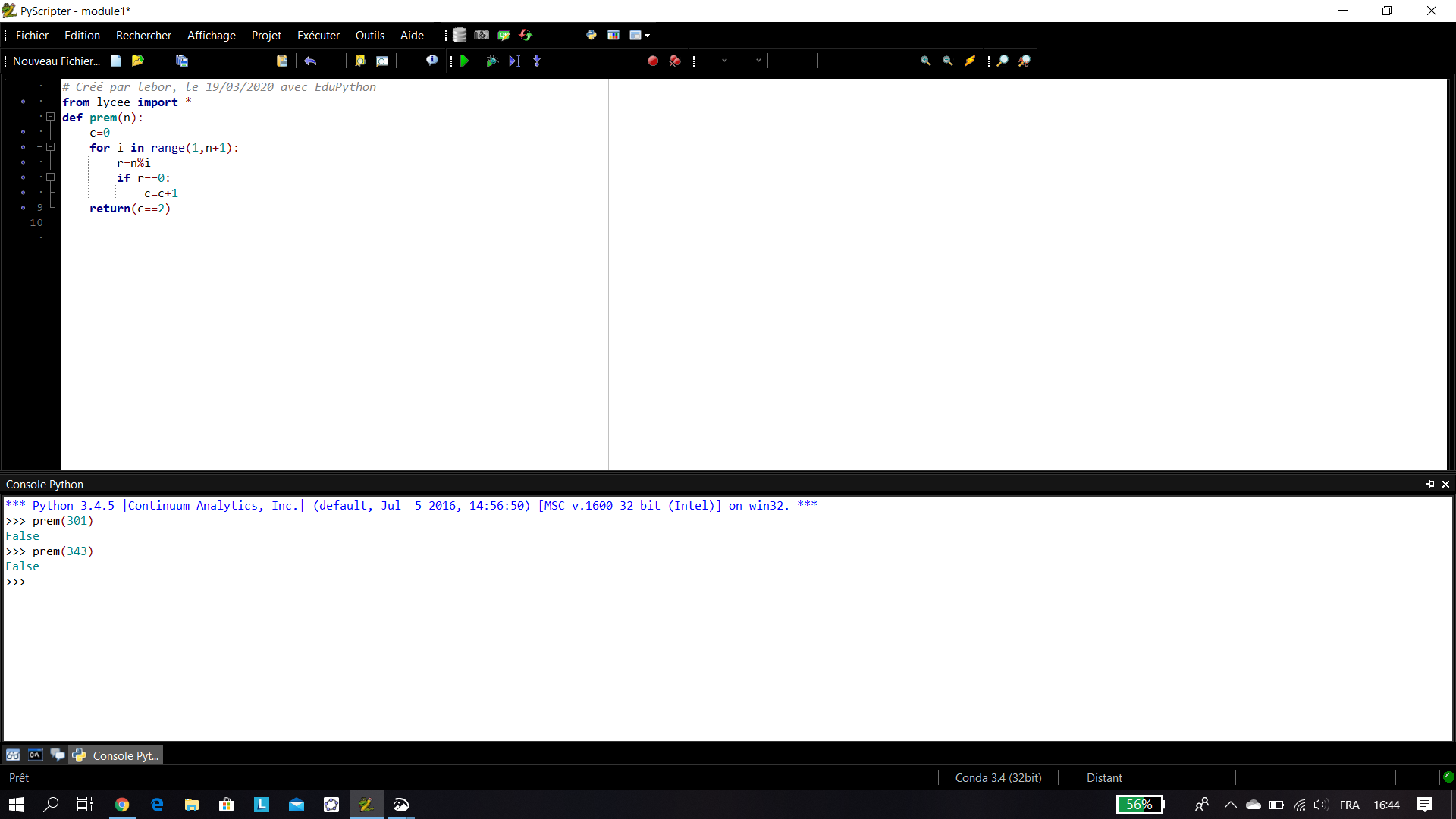
Les nombres suivants sont-ils premiers ? On pourra au besoin utiliser un algorithme écrit en langage Python.
22 27 35 36 110 125 301 334 343
Exercice n°9
Montrer que si n est impair alors n^2-1 est un multiple de 4.
Exercice n°10
Montrer que si n est un entier pair alors n^2(n+20) est un multiple de 8.