Méthode: Vous avez trouvé un facteur commun aux deux termes d’une somme, écrire les deux termes sous la forme de deux produits de deux facteurs dont l’un est commun aux deux. Utiliser le diagramme suivant.
Premier terme = facteur commun \times deuxième facteur n°1
Deuxième terme = facteur commun \timesdeuxième facteur n°2
puis écrire la somme sous la forme
facteur commun ( deuxième facteur n°1 + ( ou –) deuxième facteur n°2)
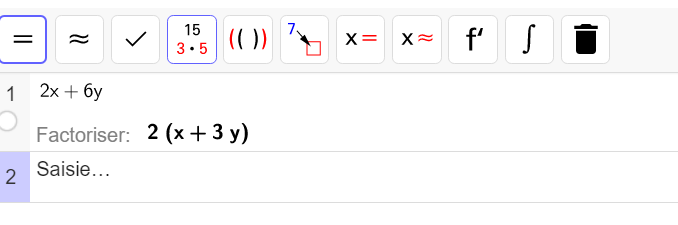
Par exemple , factorisons 2x+6y
1.Voici ce qu’il y aura sur la copie :
2x={2}\times{x}\\6y={2}\times{3y}\\2x+6y=2(x+3y)2. Un petite illustration géométrique :
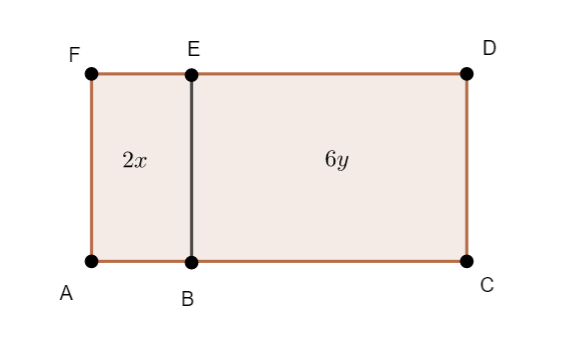
Quelle valeur la plus grande possible choisir pour la largeur AF ?
Voici la réponse :
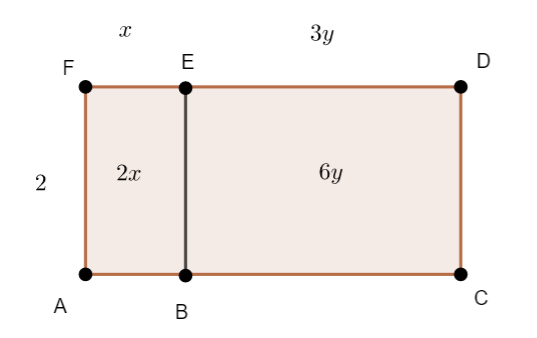
3. Valider avec l’application Calcul Formel de Géogébra :