Lorsqu’on a identifié qu’on va utiliser a^{2}+2ab +b^{2}= (a+b)^{2} pour factoriser.
Le plus simple est d’abord de compléter les pointillés ci-dessous:
a^{2}=… donc a=…\\b^{2}=… donc b=…
Ensuite je calcule le double produit 2ab en remplaçant a et b par leurs valeurs et je m’assure que le résultat obtenu est bien le troisième terme de l’expression de départ.
Pour finir, il suffit de remplacer a, b , a^{2}, 2ab et b^{2} par leurs valeurs dans :
a^{2}+2ab +b^{2}= (a+b)^{2}Factorisons par exemple, 4x^{2}+20x+25.
1. Ce qu’il doit y avoir sur la copie :
a^{2}=4x^2 donc a=2x\\b^{2}=25 donc b=5
Ensuite je calcule le double produit 2ab en remplaçant a et b par leurs valeurs et je m’assure que le résultat obtenu est bien le troisième terme de l’expression de départ.
2ab=2\times 2x\times 5=20xPour finir, il suffit de remplacer a, b , a^{2}, 2ab et b^{2} par leurs valeurs dans a^{2}+2ab +b^{2}= (a+b)^{2}\\4x^2+20x+25= (2x+5)^{2}
2. Illustration géométrique :
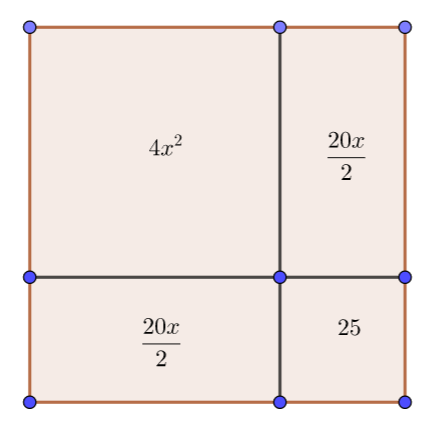
L’idée générale est la suivante : il faut voir 4x^2+20x+25 comme un calcul de l’aire du grand carré par découpage et on cherche à l’exprimer à l’aide d’une formule.
Le carré d’aire 4x^2 a pour côté 2x, le carré d’aire 25 a pour côté 5. Voyons si ça fonctionne avec les deux rectangles ?
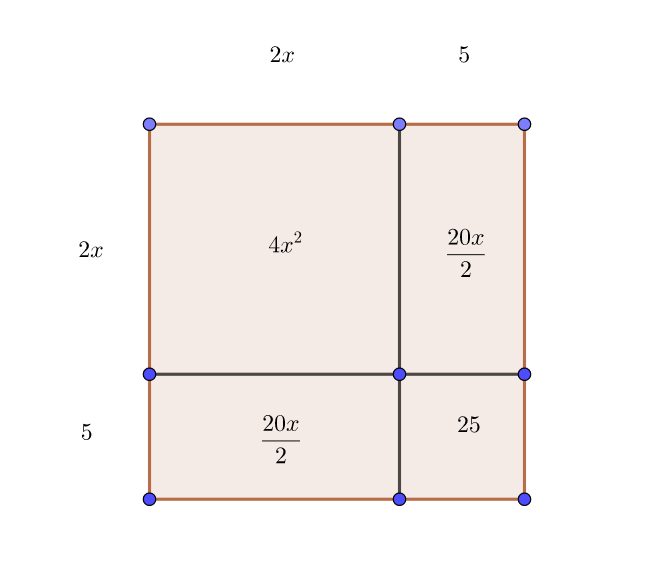
3. Valider notre réponse à l’aide de l’application Calcul Formel de géogébra.
Pour faire apparaître la page Calcul Formel dans Géogébra.
Cliquer en haut à droite de l’écran sur l’onglet représenté par trois traits horizontaux.
Cliquer sur Affichage dans le menu déroulant
Cocher la case Calcul Formel et décocher toutes les autres cases si nécessaire.




