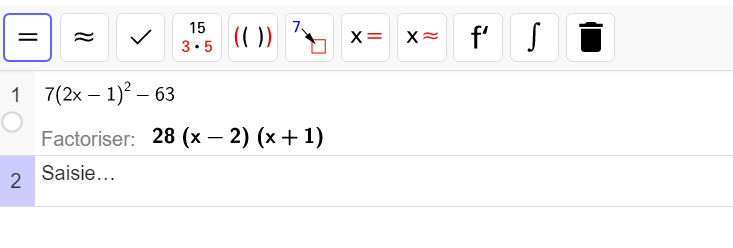
2. factoriser avec un facteur commun puis une identité remarquable.

Factoriser une expression littérale, Niveau seconde, Nombres et calculs

On se propose de factoriser $7(2x-1)^2-63$

1. Il y a un facteur commun, ici 7

Utiliser le diagramme suivant.

$7(2x-1)^2$ = $7$ $\times$ $(2x-1)^2\\63$ = $7$ $\times$ $9$

puis écrire la somme sous la forme

$7(2x-1)^2-63=$ $7$ $((2x-1)^2$ $-$ $9)$

2. on va utiliser $a^{2}-b^{2}= (a-b)(a+b)$ pour factoriser $(2x-1)^2-9$

$a^{2}=(2x-1)^2$ donc $a=2x-1\\b^{2}=9$ donc $b=3$

Pour finir, il suffit de remplacer $a$ , $b$ , $a^{2}$ et $b^{2}$ par leurs valeurs dans $a^{2}-b^{2}= (a-b)(a+b)$ .

(2x-1)^2-9= (2x-1-3)(2x-1+3)\\(2x-1)^2-9= (2x-4)(2x+2)

3. On termine :

7(2x-1)^2-63=7(2x-4)(2x+2)

4. Valider notre réponse à l’aide de l’application Calcul Formel de géogébra.

Pour faire apparaître la page Calcul Formel dans Géogébra.

Cliquer en haut à droite de l’écran sur l’onglet représenté par trois traits horizontaux.
Cliquer sur Affichage dans le menu déroulant
Cocher la case Calcul Formel et décocher toutes les autres cases si nécessaire.