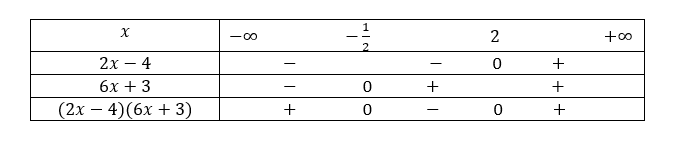logo

2.Inéquations du second degré.Exercices.

Sommaire

Exercice n°1

Résoudre dans \mathbf{R} les inéquations du second degré suivantes :

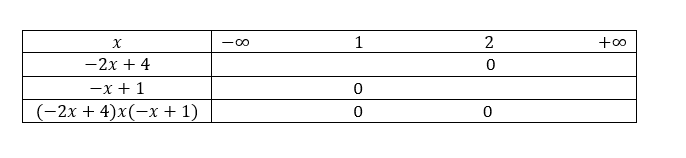
  1. (-2x+4)(-x+1)\leq 0
correction

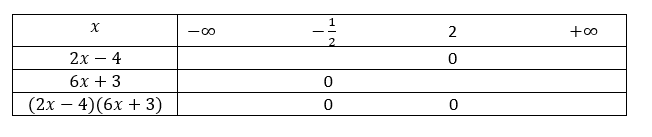
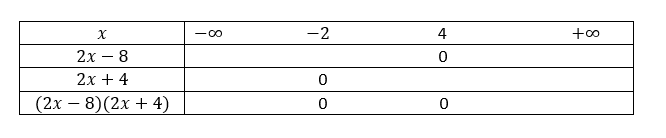
2. (2x-4)(6x+3)>0

correction

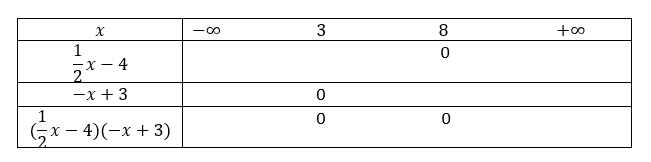
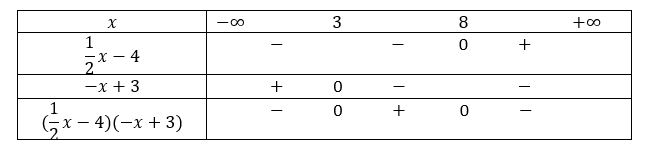
3. (\frac{1}{2}x-4)(-x+3)<0

correction

Valider vos réponses avec la page géogébra ci-dessous.

Exercice n°2

Résoudre dans \mathbf{R} les inéquations du second degré suivantes :

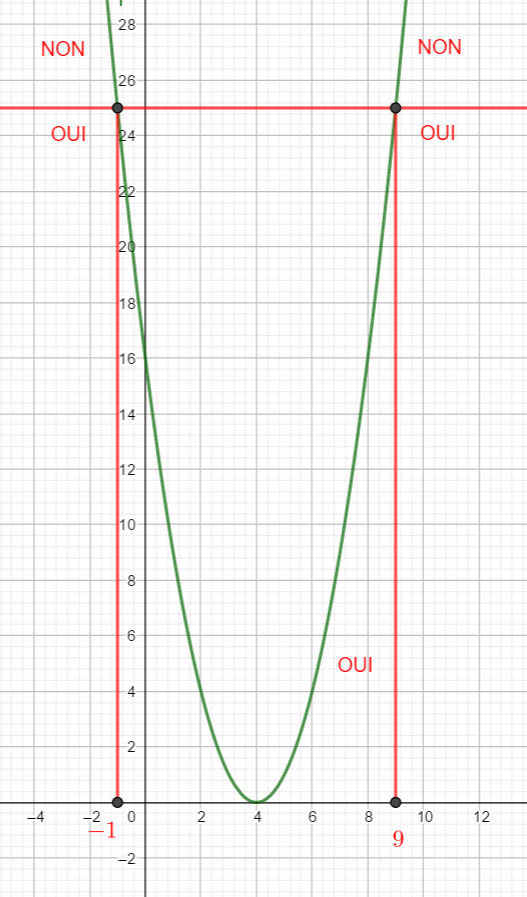
  1. (x-4)^2\leq 25
conjecture graphique
correction

2. (2x-2)^2-12>24

correction

3. (3x-1)^2-2\geq1

correction

Valider vos réponses avec la page géogébra ci-dessous.

Exercice n°3

Exercice n°3 : Résoudre dans \mathbf{R} les inéquations du second degré suivantes :

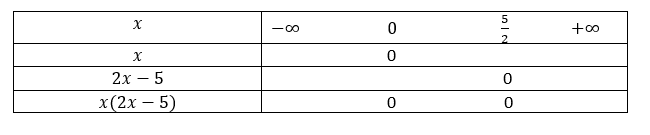
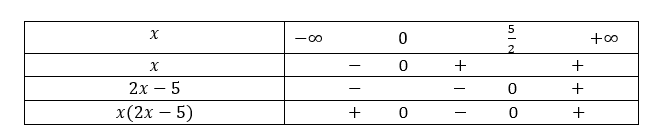
  1. 2x^2-5x+1>1
correction

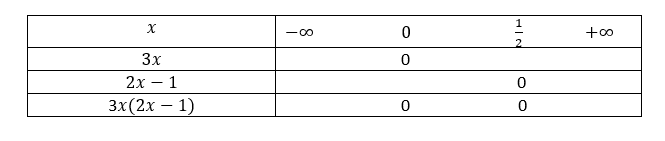
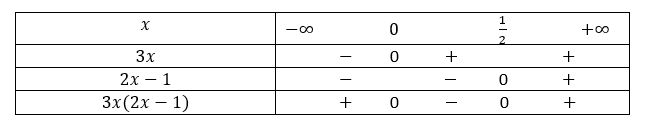
2. 6x^2-x+2\geq2x+2

correction

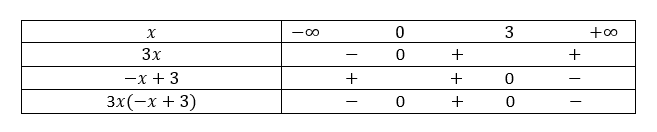
3. -3x^2+8x+5<-x+5

correction

Valider vos réponses avec la page géogébra ci-dessous.

©2020 – Math’O karé SAS

Résolvons dans \mathbf{R}, l’inéquation suivante (-2x+4)(-x+1)\leq 0

L’inéquation à résoudre (-2x+4)(-x+1)\leq 0 est du 2nd degré car en développant (-2x+4)(-x+1)  le plus grand exposant de  x est 2.

La méthode proposée concerne les inéquations du second degré.

(-2x+4)(-x+1)\leq 0

1.Je ne fais pas tout passer à gauche, zéro est déjà à droite.

2. Je ne factorise pas le membre de gauche.

3. J’écris la phrase d’introduction.

Je cherche pour quelles valeurs de x , le produit (-2x+4)(-x+1) est de signe (-) ou nul.

4. Je prépare mon tableau de signes.

Je résous -2x+4=0\\-2x=-4\\x=\frac{-4}{-2}\\x=2

Je résous -x+1=0\\-x=-1\\x=1

Je place les valeurs 1 et 2 sur la première ligne du tableau en les rangeant dans le bon ordre. Je place les zéros sur les lignes en-dessous. 

Je remplis ce tableau avec des signes (-), (+) , des zéros et parfois des doubles barres quand il y a des valeurs interdites.

On utilise le résultat du cours suivant :

Sur la ligne du facteur (-2x+4), comme a=-2 , on commence par le signe (+) jusqu’au zéro et on complète avec des (-).

Sur la ligne du facteur (-x+1), comme a=-1 , on commence par le signe (+) jusqu’au zéro et on complète avec des (-).

Pour compléter la ligne du produit (-2x+4)(-x+1), j’applique la règle des signes pour le produit.

plus par plus : plus.

plus par moins : moins.

moins par plus : moins.

moins par moins : plus.

5. Je réponds à la phrase d’introduction.

Le produit (-2x+4)(-x+1) est de signe (-) pour la seconde colonne qui correspondent aux valeurs de x comprises entre 1 et 2.

Je  prends  les valeurs 1 et 2 car le produit  peut  être nul. Donc je ferme les crochets en 1 et 2 , ce qui signifie que les crochets sont tournés vers l’intérieur de l’intervalle..

S=[1;2]

 

Résolvons dans \mathbf{R}, l’inéquation suivante (2x-4)(6x+3)>0

L’inéquation à résoudre (2x-4)(6x+3)>0 est du 2nd degré car en développant (2x-4)(6x+3)>0  le plus grand exposant de  x est 2.

La méthode proposée concerne les inéquations du second degré.

(2x-4)(6x+3)>0

1.Je ne fais pas tout passer à gauche, zéro est déjà à droite.

2. Je ne factorise pas le membre de gauche.

3. J’écris la phrase d’introduction.

Je cherche pour quelles valeurs de x , le produit (2x-4)(6x+3) est de signe (+) .

4. Je prépare mon tableau de signes.

Je résous 2x-4=0\\2x=4\\x=\frac{4}{2}\\x=2

Je résous 6x+3=0\\6x=-3\\x=-\frac{3}{6}\\x=-\frac{1}{2}

Je place les valeurs -\frac{1}{2} et 2 sur la première ligne du tableau en les rangeant dans le bon ordre. Je place les zéros sur les lignes en-dessous. 

Je remplis ce tableau avec des signes (-), (+) , des zéros et parfois des doubles barres quand il y a des valeurs interdites.

On utilise le résultat du cours suivant :

Sur la ligne du facteur (2x-4), comme a=2 , on commence par le signe (-) jusqu’au zéro et on complète avec des (+).

Sur la ligne du facteur (6x+3), comme a=6 , on commence par le signe (-) jusqu’au zéro et on complète avec des (+).

Pour compléter la ligne du produit (2x-4)(6x+3), j’applique la règle des signes pour le produit.

plus par plus : plus.

plus par moins : moins.

moins par plus : moins.

moins par moins : plus.

5. Je réponds à la phrase d’introduction.

Le produit (2x-4)(6x+3) est de signe (+) pour les première et troisième   colonnes qui correspondent aux valeurs de x comprises entre -\infty et -\frac{1}{2} puis entre 2 et +\infty.

Je  ne prends pas les valeurs -\frac{1}{2} et 2 car le produit  ne peut pas  être nul. Donc j’ouvre les crochets en -\frac{1}{2} et 2 , ce qui signifie que les crochets sont tournés vers l’extérieur de l’intervalle..

S=]-\infty;-\frac{1}{2}[\cup]2;+\infty[

 

Résolvons dans \mathbf{R}, l’inéquation suivante (\frac{1}{2}x-4)(-x+3)<0

L’inéquation à résoudre (\frac{1}{2}x-4)(-x+3)<0 est du 2nd degré car en développant (\frac{1}{2}x-4)(-x+3)  le plus grand exposant de  x est 2.

La méthode proposée concerne les inéquations du second degré.

(\frac{1}{2}x-4)(-x+3)<0

1.Je ne fais pas tout passer à gauche, zéro est déjà à droite.

2. Je ne factorise pas le membre de gauche.

3. J’écris la phrase d’introduction.

Je cherche pour quelles valeurs de x , le produit (\frac{1}{2}x-4)(-x+3) est de signe (-) .

4. Je prépare mon tableau de signes.

Je résous \frac{1}{2}x-4=0

\frac{1}{2}x=4

x=4 \times {\frac{2}{1}}\\x=8

Je résous -x+3=0\\-x=-3\\x=3

Je place les valeurs 3 et 8 sur la première ligne du tableau en les rangeant dans le bon ordre. Je place les zéros sur les lignes en-dessous. 

Je remplis ce tableau avec des signes (-), (+) , des zéros et parfois des doubles barres quand il y a des valeurs interdites.

On utilise le résultat du cours suivant :

Sur la ligne du facteur (\frac{1}{2}x-4), comme a=\frac{1}{2} , on commence par le signe (-) jusqu’au zéro et on complète avec des (+).

Sur la ligne du facteur (-x+3), comme a=-1 , on commence par le signe (+) jusqu’au zéro et on complète avec des (-).

Pour compléter la ligne du produit (\frac{1}{2}x-4)(-x+3), j’applique la règle des signes pour le produit.

plus par plus : plus.

plus par moins : moins.

moins par plus : moins.

moins par moins : plus.

5. Je réponds à la phrase d’introduction.

Le produit (\frac{1}{2}x-4)(-x+3) est de signe (-) pour les première et troisième   colonnes qui correspondent aux valeurs de x comprises entre -\infty et 3 puis entre 8 et +\infty.

Je  ne prends pas les valeurs 3 et 8 car le produit  ne peut pas  être nul. Donc j’ouvre les crochets en 3 et 8 , ce qui signifie que les crochets sont tournés vers l’extérieur de l’intervalle..

S=]-\infty;3[\cup]8;+\infty[

 

on résout graphiquement l’inéquation (x-4)^{2} \leq 25

La courbe est située sous la droite d’équation y=25 pour les valeurs de x comprises entre -1 et9.

S=[-1;9].

 

Résolvons dans \mathbf{R}, l’inéquation suivante (x-4)^{2} \leq 25

L’inéquation à résoudre (x-4)^{2} \leq 25 est du 2nd degré car en développant (x-4)^{2} le plus grand exposant de  x est 2.

La méthode proposée concerne les inéquations du second degré.

(x-4)^{2} \leq 25

1.Je fais tout passer à gauche, zéro apparaît à droite.

le 25 à droite  n’est pas à sa place, j’enlève 25 de chaque côté.

(x-4)^{2}-25 \leq 0

2. Je factorise le membre de gauche.

a. Il n’y a pas de facteur commun.

b. J’utilise l’identité remarquable a^{2}-b^{2}=(a-b)(a+b) pour factoriser (x-4)^{2}-25

a^{2}=(x-4)^{2} \hspace{2cm}a=(x-4)

b^{2}=25\hspace{3.2cm}b=5

Je remplace a et b par (x-4) et 5 dans a^{2}-b^{2}=(a-b)(a+b)

((x-4)-5)((x-4)+5) \leq 0\\(x-9)(x+1) \leq 0

3. J’écris la phrase d’introduction.

 Je cherche pour quelles valeurs de x, le produit (x-9)(x+1) est de signe(-) ou nul.

4. Je prépare mon tableau de signes.

Je résous x-9=0\\x=9

Je résous x+1=0\\x=-1

Je place les valeurs -1 et 9 sur la première ligne du tableau en les rangeant dans le bon ordre. Je place les zéros sur les lignes en-dessous. 

Je remplis ce tableau avec des signes (-), (+) , des zéros et parfois des doubles barres quand il y a des valeurs interdites.

On utilise le résultat du cours suivant :

Sur la ligne du facteur (x-9), comme a=1 , on commence par le signe (-) jusqu’au zéro et on complète avec des (+).

Sur la ligne du facteur (x+1), comme a=1 , on commence par le signe (-) jusqu’au zéro et on complète avec des (+).

Pour compléter la ligne du produit (x-9)(x+1), j’applique la règle des signes pour le produit.

plus par plus : plus.

plus par moins : moins.

moins par plus : moins.

moins par moins : plus.

5. Je réponds à la phrase d’introduction.

Le produit (x-9)(x+1) est de signe(-) pour la deuxième colonne qui correspond aux valeurs de x comprises entre -1 et 9.

Je  prends  les valeurs -1 et 9 car le produit  peut  être nul. Donc je ferme les crochets en -1 et 9, ce qui signifie que les crochets sont tournés vers l’intérieur.

S=[-1;9]

 

Résolvons dans \mathbf{R}, l’inéquation suivante (2x-2)^{2}-12 >24

L’inéquation à résoudre (2x-2)^{2}-12 >24 est du 2nd degré car en développant (2x-2)^{2} le plus grand exposant de  x est 2.

La méthode proposée concerne les inéquations du second degré.

(2x-2)^{2}-12 >24

1.Je fais tout passer à gauche, zéro apparaît à droite.

le 24 à droite n’est pas à sa place, j’enlève 24 de chaque côté.

(2x-2)^{2}-12 -24>0

(2x-2)^{2}-36>0

2. Je factorise le membre de gauche.

a. Il n’y a pas de facteur commun.

b. J’utilise l’identité remarquable a^{2}-b^{2}=(a-b)(a+b) pour factoriser (2x-2)^{2}-36

a^{2}=(2x-2)^{2} \hspace{2cm}a=(2x-2)

b^{2}=36\hspace{3.2cm}b=6

Je remplace a et b par (2x-2) et 6 dans a^{2}-b^{2}=(a-b)(a+b)

((2x-2)-6)((2x-2)+6) >0\\(2x-8)(2x+4) >0

3. J’écris la phrase d’introduction.

 Je cherche pour quelles valeurs de x, le produit (2x-8)(2x+4) est de signe(+) .

4. Je prépare mon tableau de signes.

Je résous 2x-8=0\\2x=8\\x=\frac{8}{2}\\x=4

Je résous 2x+4=0\\2x=-4\\x=-\frac{4}{2}\\x=-2

Je place les valeurs -2 et 4 sur la première ligne du tableau en les rangeant dans le bon ordre. Je place les zéros sur les lignes en-dessous. 

Je remplis ce tableau avec des signes (-), (+) , des zéros et parfois des doubles barres quand il y a des valeurs interdites.

On utilise le résultat du cours suivant :

Sur la ligne du facteur (2x-8), comme a=2 , on commence par le signe (-) jusqu’au zéro et on complète avec des (+).

Sur la ligne du facteur (2x+4), comme a=2 , on commence par le signe (-) jusqu’au zéro et on complète avec des (+).

Pour compléter la ligne du produit (2x-8)(2x+4), j’applique la règle des signes pour le produit.

plus par plus : plus.

plus par moins : moins.

moins par plus : moins.

moins par moins : plus.

5. Je réponds à la phrase d’introduction.

Le produit (2x-8)(2x+4) est de signe(+) pour les première et troisième colonnes qui correspondent aux valeurs de x comprises entre -\infty et -2 puis entre 4 et +\infty.

Je  ne prends pas les valeurs -2 et 4 car le produit  ne peut pas être nul. Donc j’ouvre les crochets en -2 et 4, ce qui signifie que les crochets sont tournés vers l’extérieur.

S=]-\infty;-2[ \cup]4;+\infty[

 

Résolvons dans \mathbf{R}, l’inéquation suivante (3x-1)^{2}-2 \geq 1

L’inéquation à résoudre (3x-1)^{2}-2 \geq 1 est du 2nd degré car en développant (3x-1)^{2} le plus grand exposant de  x est 2.

La méthode proposée concerne les inéquations du second degré.

(3x-1)^{2}-2 \geq 1

1.Je fais tout passer à gauche, zéro apparaît à droite.

le 1 à droite  n’est pas à sa place, j’enlève 1 de chaque côté.

(3x-1)^{2}-2-1 \geq 0

(3x-1)^{2}-3 \geq 0

2. Je factorise le membre de gauche.

a. Il n’y a pas de facteur commun.

b. J’utilise l’identité remarquable a^{2}-b^{2}=(a-b)(a+b) pour factoriser (3x-1)^{2}-3

a^{2}=(3x-1)^{2} \hspace{2cm}a=(3x-1)

b^{2}=3\hspace{3.2cm}b=\sqrt{3}

Je remplace a et b par (3x-1) et \sqrt{3} dans a^{2}-b^{2}=(a-b)(a+b)

((3x-1)-\sqrt{3})((3x-1)+\sqrt{3}) \geq 0

(3x-1-\sqrt{3})(3x-1+\sqrt{3}) \geq 0

3. J’écris la phrase d’introduction.

 Je cherche pour quelles valeurs de x, le produit (3x-1-\sqrt{3})(3x-1+\sqrt{3}) est de signe(+) ou nul.

4. Je prépare mon tableau de signes.

Je résous 3x-1-\sqrt{3} =0

3x=1+\sqrt{3}

x=\frac{1+\sqrt{3}}{3}

Je résous 3x-1+\sqrt{3} =0

3x=1-\sqrt{3}

x=\frac{1-\sqrt{3}}{3}

Je place les valeurs \frac{1-\sqrt{3}}{3} et \frac{1+\sqrt{3}}{3} sur la première ligne du tableau en les rangeant dans le bon ordre. Je place les zéros sur les lignes en-dessous. 

Je remplis ce tableau avec des signes (-), (+) , des zéros et parfois des doubles barres quand il y a des valeurs interdites.

On utilise le résultat du cours suivant :

Sur la ligne du facteur 3x-1-\sqrt{3}, comme a=3 , on commence par le signe (-) jusqu’au zéro et on complète avec des (+).

Sur la ligne du facteur 3x-1+\sqrt{3} , comme a=3 , on commence par le signe (-) jusqu’au zéro et on complète avec des (+).

Pour compléter la ligne du produit (3x-1-\sqrt{3})(3x-1+\sqrt{3}) , j’applique la règle des signes pour le produit.

plus par plus : plus.

plus par moins : moins.

moins par plus : moins.

moins par moins : plus.

5. Je réponds à la phrase d’introduction.

Le produit (3x-1-\sqrt{3})(3x-1+\sqrt{3}) est de signe(+) pour les première et troisième colonnes qui correspondent aux valeurs de x comprises entre -\infty et \frac{1-\sqrt{3}}{3} puis entre -\frac{1+\sqrt{3}}{3} et +\infty.

Je  prends  les valeurs \frac{1-\sqrt{3}}{3} et \frac{1+\sqrt{3}}{3} car le produit  peut  être nul. Donc je ferme les crochets en \frac{1-\sqrt{3}}{3} et \frac{1+\sqrt{3}}{3}, ce qui signifie que les crochets sont tournés vers l’intérieur.

S=]-\infty;\frac{1-\sqrt{3}}{3}]\cup[\frac{1+\sqrt{3}}{3};+\infty[

 

Résolvons dans \mathbf{R}, l’inéquation suivante 2x^{2}-5x+1 >1

L’inéquation à résoudre 2x^{2}-5x+1 >1 est du 2nd degré . Dans  2x^{2}-5x+1 le plus grand exposant de  x est 2.

La méthode proposée concerne les inéquations du second degré.

2x^{2}-5x+1 >1

1.Je fais tout passer à gauche, zéro apparaît à droite.

le 1 à droite  n’est pas à sa place, j’enlève 1 de chaque côté.

2x^{2}-5x+1-1 >0

2x^{2}-5x >0

2. Je factorise le membre de gauche.

a. Il y a un facteur commun.

2x^{2}= {x}\times{2x}

5x ={x}\times{5}

x(2x-5) > 0

3. J’écris la phrase d’introduction.

 Je cherche pour quelles valeurs de x, le produit x(2x-5) est de signe(+) .

4. Je prépare mon tableau de signes.

Je résous x=0

 Je résous 2x-5=0\\2x=5\\x=\frac{5}{2}

Je place les valeurs 0 et \frac{5}{2} sur la première ligne du tableau en les rangeant dans le bon ordre. Je place les zéros sur les lignes en-dessous. 

Je remplis ce tableau avec des signes (-), (+) , des zéros et parfois des doubles barres quand il y a des valeurs interdites.

On utilise le résultat du cours suivant :

Sur la ligne du facteur x, comme a=1 , on commence par le signe (-) jusqu’au zéro et on complète avec des (+).

Sur la ligne du facteur (2x-5), comme a=2 , on commence par le signe (-) jusqu’au zéro et on complète avec des (+).

Pour compléter la ligne du produit x(2x-5), j’applique la règle des signes pour le produit.

plus par plus : plus.

plus par moins : moins.

moins par plus : moins.

moins par moins : plus.

5. Je réponds à la phrase d’introduction.

Le produit x(2x-5) est de signe(+) pour les première et troisième colonnes  qui correspondent aux valeurs de x comprises entre -\infty et 0 puis entre \frac{5}{2} et +\infty.

Je  ne prends pas les valeurs 0 et \frac{5}{2} car le produit  ne peut pas être nul. Donc j’ouvre les crochets en 0 et \frac{5}{2}, ce qui signifie que les crochets sont tournés vers l’extérieur de l’intervalle.

S=]-\infty;0[\cup]\frac{5}{2};+\infty[

 

Résolvons dans \mathbf{R}, l’inéquation suivante 6x^{2}-x+2 \geq2x+2

L’inéquation à résoudre 6x^{2}-x+2 \geq2x+2 est du 2nd degré car le plus grand exposant de  x est 2.

La méthode proposée concerne les inéquations du second degré.

6x^{2}-x+2 \geq2x+2

1.Je fais tout passer à gauche, zéro apparaît à droite.

le 2x+2 à droite  n’est pas à sa place, j’enlève 2x+2 de chaque côté.

6x^{2}-x+2 -2x-2\geq0

6x^{2}-3x\geq 0

2. Je factorise le membre de gauche.

a. Il y a un facteur commun.

6x^{2}= {3x}\times{2x}

3x ={3x}\times{1}

3x(2x-1) \geq0

3. J’écris la phrase d’introduction.

 Je cherche pour quelles valeurs de x, le produit 3x(2x-1) est de signe(+) ou nul .

4. Je prépare mon tableau de signes.

Je résous 3x=0\\x=\frac{0}{3}\\x=0

 Je résous 2x-1=0\\2x=1\\x=\frac{1}{2}

Je place les valeurs 0 et \frac{1}{2} sur la première ligne du tableau en les rangeant dans le bon ordre. Je place les zéros sur les lignes en-dessous. 

Je remplis ce tableau avec des signes (-), (+) , des zéros et parfois des doubles barres quand il y a des valeurs interdites.

On utilise le résultat du cours suivant :

Sur la ligne du facteur 3x, comme a=3 , on commence par le signe (-) jusqu’au zéro et on complète avec des (+).

Sur la ligne du facteur (2x-1), comme a=2 , on commence par le signe (-) jusqu’au zéro et on complète avec des (+).

Pour compléter la ligne du produit 3x(2x-1), j’applique la règle des signes pour le produit.

plus par plus : plus.

plus par moins : moins.

moins par plus : moins.

moins par moins : plus.

5. Je réponds à la phrase d’introduction.

Le produit 3x(2x-1) est de signe(+) pour les première et troisième colonnes  qui correspondent aux valeurs de x comprises entre -\infty et 0 puis entre \frac{1}{2} et +\infty.

Je prends les valeurs 0 et \frac{1}{2} car le produit   peut  être nul. Donc je ferme les crochets en 0 et \frac{1}{2}, ce qui signifie que les crochets sont tournés vers l’intérieur de l’intervalle.

S=]-\infty;0]\cup[\frac{1}{2};+\infty[

 

Résolvons dans \mathbf{R}, l’inéquation suivante -3x^{2}+8x+5 <-x+5

L’inéquation à résoudre -3x^{2}+8x+5 <-x+5 est du 2nd degré car le plus grand exposant de  x est 2.

La méthode proposée concerne les inéquations du second degré.

-3x^{2}+8x+5 <-x+5

1.Je fais tout passer à gauche, zéro apparaît à droite.

le -x+5 à droite  n’est pas à sa place, j’enlève -x+5 de chaque côté.

-3x^{2}+8x+5+x-5 <0

-3x^{2}+9x<0

2. Je factorise le membre de gauche.

a. Il y a un facteur commun.

-3x^{2}= {3x}\times{(-x)}

9x ={3x}\times{3}

3x(-x+3)<0

3. J’écris la phrase d’introduction.

 Je cherche pour quelles valeurs de x, le produit 3x(-x+3) est de signe(-) .

4. Je prépare mon tableau de signes.

Je résous 3x=0\\x=\frac{0}{3}\\x=0

 Je résous -x+3=0\\-x=-3\\x=\frac{-3}{-1}\\x=3

Je place les valeurs 0 et 3 sur la première ligne du tableau en les rangeant dans le bon ordre. Je place les zéros sur les lignes en-dessous. 

Je remplis ce tableau avec des signes (-), (+) , des zéros et parfois des doubles barres quand il y a des valeurs interdites.

On utilise le résultat du cours suivant :

Sur la ligne du facteur 3x, comme a=3 , on commence par le signe (-) jusqu’au zéro et on complète avec des (+).

Sur la ligne du facteur (-x+3), comme a=-1 , on commence par le signe (+) jusqu’au zéro et on complète avec des (-).

Pour compléter la ligne du produit 3x(-x+3), j’applique la règle des signes pour le produit.

plus par plus : plus.

plus par moins : moins.

moins par plus : moins.

moins par moins : plus.

5. Je réponds à la phrase d’introduction.

Le produit 3x(-x+3) est de signe(-) pour les première et troisième colonnes  qui correspondent aux valeurs de x comprises entre -\infty et 0 puis entre 3 et +\infty.

Je ne prends pas les valeurs 0 et 3 car le produit   ne peut pas être nul. Donc j’ouvre les crochets en 0 et 3, ce qui signifie que les crochets sont tournés vers l’extérieur de l’intervalle.

S=]-\infty;0[\cup]3;+\infty[

 

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.