En 2016, une entreprise compte produire au plus 60 000 téléphones mobiles pour la France et les
vendre 800 euros l’unité. On supposera que tous les téléphones produits sont vendus. On s’intéressera dans cet exercice au bénéfice éventuel réalisé par l’entreprise.
Après plusieurs études, les coûts, en euros, liés à la production, à la distribution et à la publicité, sont
modélisés par
C(x) = 0,01x^2 +250x +2500000
(où x est le nombre d’exemplaires fabriqués et vendus).
Combien l’entreprise doit fabriquer de téléphones pour être bénéficiaire ?
Une entreprise réalise un bénéfice lorsque la recette est srictement supérieure aux coûts de production.
Question préliminaire: On note R(x) la recette générée par la vente de x téléphones.
Exprimer R(x) en fonction de x.
Méthode n°1: Déterminer pour quelles valeurs de x la courbe R est au-dessus et pas sur la courbe C.
Pour cela utiliser la fenêtre Géogébra ci-dessous. Pour modifier les graduations sur les axes, cliquer gauche dans le repère et sélectionner Graphique dans le menu déroulant. Paramétrer ensuite l’affichage de votre fenêtre.
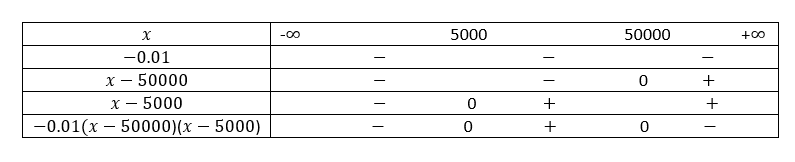
Méthode n°2: Résoudre R(x)>C(x) par le calcul.
On peut conjecturer le résultat à l’aide de la fenêtre Géogébra avec l’application Calcul formel.
Conseil :Après avoir fait apparaître le zéro à droite, utiliser l’application Calcul Formel de Géogébra pour factoriser le membre de gauche.