logo

2. Equation réduite. Exercices.

Sommaire

Exercice 1 

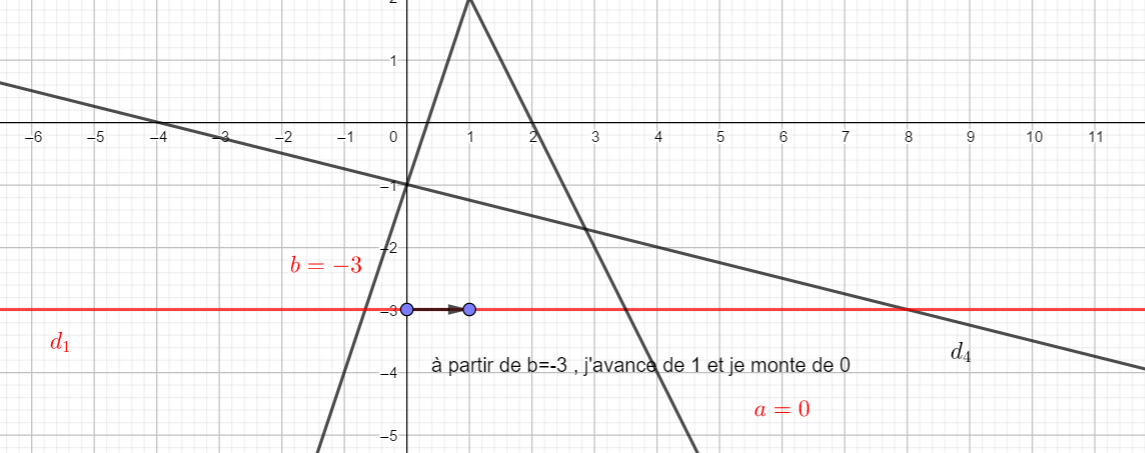
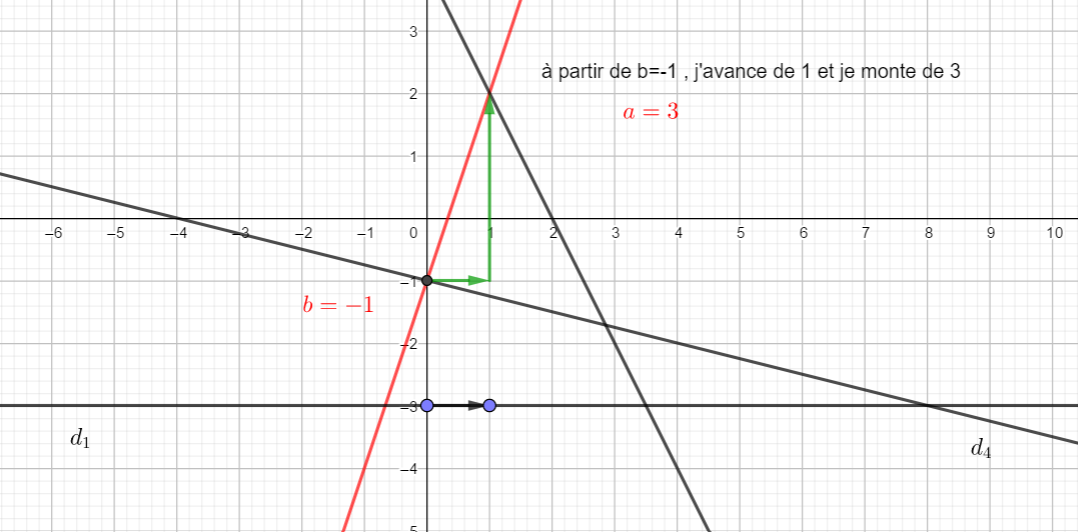
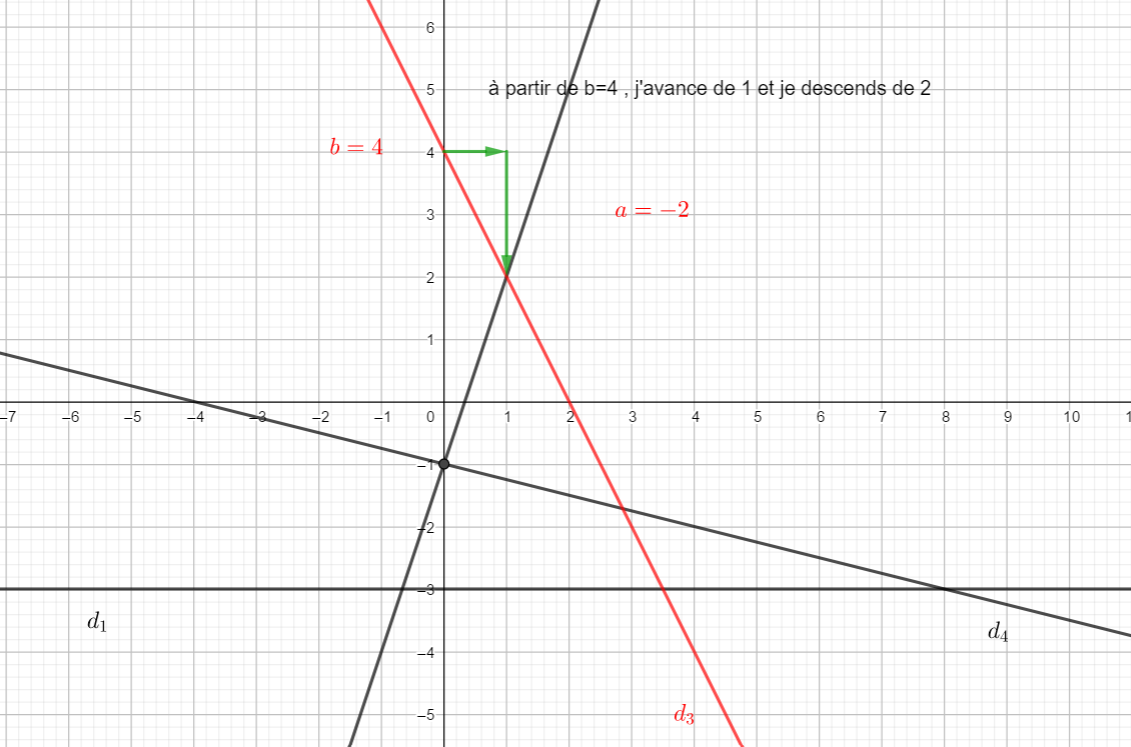
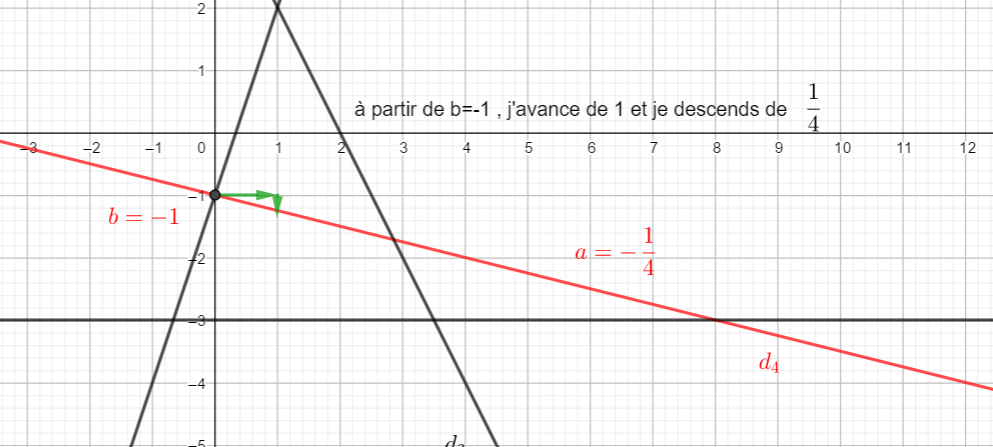
Déterminer graphiquement dans chaque cas, l’équation réduite (si elle existe) de chaque droite.

correction d_1
correction d_2
correction d_3
correction d_4

Vidéo : déterminer quand c’est possible l’équation réduite d’une droite.

Exercice n°2

Déterminer l’équation réduite de d quand c’est possible. On pourra utiliser Géogébra pour conjecturer l’équation réduite. Pour cela on crée deux points A et B dans le repère, on trace la droite qui passe par ces deux points et on lit son équation réduite dans la colonne algèbre. Dans la fenêtre ci-dessous tout est déjà configuré. Il ne reste qu’à cliquer sur le premier onglet en haut à gauche (le flèche) et sélectionner Déplacer dans le menu déroulant. Puis on déplace les points A et B pour obtenir ceux de l’énoncé . Par exemple dans la question 1 on a A(1;3) et B(5;-1). Ne pas hésiter à utiliser le 11ème onglet et sélectionner Déplacer graphique si nécessaire. 

  1. d passe par A(1;3) et B(5;-1)
correction

2. d passe par A(-1;3) et B(1;-2)

correction

3. d passe par A(-1;1) et B(4;-1)

correction

4. d passe par A(-2;3) et B(7;3)

correction

5. d passe par A(-3;3) et B(-3;9)

correction

Exercice n°3

Déterminer l’équation réduite de d quand c’est possible.

1. d passe par C(1;3) et a pour coefficient directeur 2

correction

2. d passe par C(0;2) et a pour coefficient directeur -1

correction

3. d passe par C(\frac{1}{2};\frac{2}{5}) et a pour coefficient directeur -5

correction

4. d passe par C(-1;-2) et a pour coefficient directeur 0

correction

5. d passe par C(-2;-3) et a pour coefficient directeur 1

correction

Exercice n°4

Déterminer l’équation réduite de d quand c’est possible.

1. d passe par E(-1;0) et est parallèle à la droite d’équation y=x-3

correction

2. d passe par E(0;\frac{1}{2}) et est parallèle à la droite d’équation y=-2x+1

correction

3. d passe par E(-\frac{1}{2};2) et est parallèle à la droite d’équation y=3

correction

4. d passe par E(1;1) et est parallèle à la droite d’équation y=-\frac{1}{2}x+2

correction

5. d passe par E(-2;-3) et est parallèle à la droite d’équation y=\frac{2}{3}x-1

correction

Exercice n°5

Déterminer l’équation réduite de d quand c’est possible.

1. d passe par E(-2;-1) et a pour ordonnée à l’origine 3

correction méthode n°1
correction méthode n°2

2. d passe par E(\frac{1}{2};3) et a pour ordonnée à l’origine 2

correction méthode n°1
correction méthode n°2

3. d passe par E(6;-1) et a pour ordonnée à l’origine -1

correction méthode n°1
correction méthode n°2

4. d passe par E(8;0) et a pour ordonnée à l’origine -\frac{1}{2}

correction méthode n°1
correction méthode n°2

5. d passe par E(\frac{1}{5};\frac{1}{4}) et a pour ordonnée à l’origine 0

correction méthode n°1
correction méthode n°2

©2020 – Math’O karé SAS

Déterminons l’équation réduite de d_1

La droite d_1coupe l’axe des ordonnées en -3 donc b=-3.

A partir du point de la droite de coordonnées (0;-3) , j’avance horizontalement de 1 vers la droite. Pour retomber sur la droite, je ne monte pas, je ne descends pas  donc a=0

Je remplace a  et b par 0 et -3 dans l’équation générale y=ax+b donc :

L’équation réduite de  d_1 est  y=0x-3   ou y=-3.

 

Déterminons l’équation réduite de d_2

La droite d_2 coupe l’axe des ordonnées en -1 donc b=-1.

A partir du point de la droite de coordonnées (0;-1) , j’avance horizontalement de 1 vers la droite. Pour retomber sur la droite, je ne monte de 3 donc a=3

Je remplace a  et b par 3 et -1 dans l’équation générale y=ax+b donc :

L’équation réduite de  d_2 est  y=3x-1 .

 

Déterminons l’équation réduite de d_3

La droite d_3 coupe l’axe des ordonnées en 4 donc b=4.

A partir du point de la droite de coordonnées (0;4) , j’avance horizontalement de 1 vers la droite. Pour retomber sur la droite, je descends de 2 donc a=-2

Je remplace a  et b par -2 et 4 dans l’équation générale y=ax+b donc :

L’équation réduite de  d_3 est  y=-2x+4 .

Déterminons l’équation réduite de d_4

La droite d_4 coupe l’axe des ordonnées en -1 donc b=-1.

A partir du point de la droite de coordonnées (0;-1) , j’avance horizontalement de 1 vers la droite. Pour retomber sur la droite, je descends de \frac{1}{4} donc a=-\frac{1}{4}

Je remplace a  et b par -\frac{1}{4} et -1 dans l’équation générale y=ax+b donc :

L’équation réduite de  d_4 est  y=-\frac{1}{4}x-1 .

 

d passe par A(1;3) B(5;-1)

On n’hésite pas à repérer les coordonnées des points A et B ainsi

\hspace{0.3cm} x_{A} y_{A} \hspace{0.4cm} x_{B} y_{B}

A(1;3) \hspace{0.2cm} B(5;-1)

Je compare x_{A} et x_{B}

x_{A} \neq x_{B} car   1 \neq 5

Je peux donc calculer le coefficient directeur , en utilisant la formule suivante:

a=\frac{y_{B}-y_{A}} {x_{B}-x_{A}}

On prend soin ensuite de remplacer les lettres par les bons nombres. Si le nombre est négatif, je prends l’habitude de l’écrire entre parenthèses.

a=\frac{(-1)-3} {5-1} \\ a=\frac{-4} {4} \\ a=-1

Je calcule ensuite l’ordonnée à l’origine, en utilisant la formule suivante:

b= y_{A} – ax_{A}

On prend soin ensuite de remplacer les lettres par les bons nombres. Si le nombre est négatif, je prends l’habitude de l’écrire entre parenthèses.

b=3-(-1)\times1

Dans cette suite d’opérations, on effectue d’abord le produit puis la somme :

b=3+1=4

Pour finir je remplace a et b par -1 et 4 dans l’équation réduite y=ax+b

L’équation de la droite d est

y= (-1) x+ 4\\ y=-x+4

 

d passe par A(-1;3) B(1;-2)

On n’hésite pas à repérer les coordonnées des points A et B ainsi

\hspace{0.4cm} x_{A} y_{A} \hspace{0.8cm} x_{B} y_{B}

A(-1;3) \hspace{0.4cm} B(1;-2)

Je compare x_{A} et x_{B}

x_{A} \neq x_{B} car   -1 \neq 1

Je peux donc calculer le coefficient directeur , en utilisant la formule suivante:

a=\frac{y_{B}-y_{A}} {x_{B}-x_{A}}

On prend soin ensuite de remplacer les lettres par les bons nombres. Si le nombre est négatif, je prends l’habitude de l’écrire entre parenthèses.

a=\frac{(-2)-3} {1-(-1)} \\ a=\frac{-5} {2}

Je calcule ensuite l’ordonnée à l’origine, en utilisant la formule suivante:

b= y_{A} – ax_{A}

On prend soin ensuite de remplacer les lettres par les bons nombres. Si le nombre est négatif, je prends l’habitude de l’écrire entre parenthèses.

b=3-(\frac{-5} {2})\times(-1) \\b=3-\frac{5} {2}

Pour calculer 3-\frac{5} {2}, il faut mettre au même dénominateur, ici 2.

b={3}\times {\frac{2} {2}} -\frac{5} {2}\\b=\frac{6} {2} -\frac{5} {2}\\b=\frac{1} {2}

Pour finir je remplace a et b par -\frac{5} {2} et \frac{1} {2} dans l’équation réduite y=ax+b

L’équation de la droite d est y= -\frac{5} {2}x+ \frac{1} {2}

 

 

d passe par A(-1;1) B(4;-1)

On n’hésite pas à repérer les coordonnées des points A et B ainsi

\hspace{0.4cm} x_{A} y_{A} \hspace{0.8cm} x_{B} y_{B}

A(-1;1) \hspace{0.4cm} B(4;-1)

Je compare x_{A} et x_{B}

x_{A} \neq x_{B} car   -1 \neq 4

Je peux donc calculer le coefficient directeur , en utilisant la formule suivante:

a=\frac{y_{B}-y_{A}} {x_{B}-x_{A}}

On prend soin ensuite de remplacer les lettres par les bons nombres. Si le nombre est négatif, je prends l’habitude de l’écrire entre parenthèses.

a=\frac{(-1)-1} {4-(-1)} \\a=\frac{-2} {5}

Je calcule ensuite l’ordonnée à l’origine, en utilisant la formule suivante:

b= y_{A} – ax_{A}

On prend soin ensuite de remplacer les lettres par les bons nombres. Si le nombre est négatif, je prends l’habitude de l’écrire entre parenthèses.

b=1-(-\frac{2} {5})\times(-1) \\b=1-\frac{2} {5}

Pour calculer 1-\frac{2} {5}, il faut mettre au même dénominateur, ici 5.

b={1}\times {\frac{5} {5}} -\frac{2} {5}\\b=\frac{5} {5} -\frac{2} {5}\\b=\frac{3} {5}

Pour finir je remplace a et b par -\frac{2} {5} et \frac{3} {5} dans l’équation réduite y=ax+b

L’équation de la droite d est y= -\frac{2} {5}x+ \frac{3} {5}

 

 

d passe par A(-2;3) B(7;3)

On n’hésite pas à repérer les coordonnées des points A et B ainsi

\hspace{0.4cm} x_{A} y_{A} \hspace{0.7cm} x_{B} y_{B}

A(-2;3) \hspace{0.4cm} B(7;3)

Je compare x_{A} et x_{B}

x_{A} \neq x_{B} car -2 \neq 7

Je peux donc calculer le coefficient directeur , en utilisant la formule suivante:

a=\frac{y_{B}-y_{A}} {x_{B}-x_{A}}

On prend soin ensuite de remplacer les lettres par les bons nombres. Si le nombre est négatif, je prends l’habitude de l’écrire entre parenthèses.

a=\frac{3-3} {7-(-2)} \\ a=\frac{0} {9} \\ a=0

Je calcule ensuite l’ordonnée à l’origine, en utilisant la formule suivante:

b= y_{A} – ax_{A}

On prend soin ensuite de remplacer les lettres par les bons nombres. Si le nombre est négatif, je prends l’habitude de l’écrire entre parenthèses.

b=3-0\times(-2) \\b=3

Pour finir je remplace a et b par 0 et 3 dans l’équation réduite y=ax+b

L’équation de la droite d est y= 0x+ 3 ou y= 3 

 

 

 

d passe par A(-3;3) B(-3;9)

On n’hésite pas à repérer les coordonnées des points A et B ainsi

\hspace{0.4cm} x_{A} y_{A} \hspace{0.8cm} x_{B} y_{B}

A(-3;3) \hspace{0.4cm} B(-3;9)

Je compare x_{A} et x_{B}

x_{A} = x_{B} car -3=-3

Donc la droite d n’admet pas d’équation réduite.

 

d passe par C(1;3) et a pour coefficient directeur 2

D’après l’énoncé le coefficient directeur a=2

On n’hésite pas à repérer les coordonnées du point C ainsi

\hspace{0.3cm} x_{C} y_{C}

C(1;3)

Je calcule l’ordonnée à l’origine, en utilisant la formule suivante ( ici, c’est : C qui est le point de la droite d )

b= y_{C} – ax_{C}

On prend soin ensuite de remplacer les lettres par les bons nombres. Si le nombre est négatif, je prends l’habitude de l’écrire entre parenthèses.

b= y_{C} – ax_{C} \\b=3-2\times1 \\b=3-2 \\ b=1

Pour finir je remplace a et b par 2 et 1 dans l’équation réduite y=ax+b

L’équation de la droite d est y= 2 x+1

 

 

d passe par C(0;2) et a pour coefficient directeur -1

D’après l’énoncé le coefficient directeur a=-1

On n’hésite pas à repérer les coordonnées du point C ainsi

\hspace{0.3cm} x_{C} y_{C}

C(0;2)

Je calcule l’ordonnée à l’origine, en utilisant la formule suivante ( ici, c’est : C qui est le point de la droite d )

b= y_{C} – ax_{C}

On prend soin ensuite de remplacer les lettres par les bons nombres. Si le nombre est négatif, je prends l’habitude de l’écrire entre parenthèses.

b= y_{C} – ax_{C} \\b=2-(-1)\times0 \\b=2-0 \\b=2

Pour finir je remplace a et b par -1 et 2 dans l’équation réduite y=ax+b

L’équation de la droite d est y= -1 x+2 ou y= -x+2  

 

 

d passe par C(\frac{1}{2};\frac{2}{5}) et a pour coefficient directeur -5

D’après l’énoncé le coefficient directeur a=-5

On n’hésite pas à repérer les coordonnées du point C ainsi

\hspace{0.4cm} x_{C} y_{C}

C(\frac{1}{2};\frac{2}{5})

Je calcule l’ordonnée à l’origine, en utilisant la formule suivante ( ici, c’est : C qui est le point de la droite d )

b= y_{C} – ax_{C}

On prend soin ensuite de remplacer les lettres par les bons nombres. Si le nombre est négatif, je prends l’habitude de l’écrire entre parenthèses.

b= y_{C} – ax_{C} \\b=\frac{2}{5}-(-5)\times{ \frac{1}{2}}\\b=\frac{2}{5}+ \frac{5}{2}\\b={\frac{2}{5}}\times {\frac{2}{2}}+ {\frac{5}{2}}\times {\frac{5}{5}}\\b=\frac{4}{10}+ \frac{25}{10}\\b=\frac{29}{10}

Pour finir je remplace a et b par -5 et \frac{29}{10} dans l’équation réduite y=ax+b

L’équation de la droite d est y= -5 x+\frac{29}{10}  

 

 

d passe par C(-1;-2) et a pour coefficient directeur 0

D’après l’énoncé le coefficient directeur a=0

On n’hésite pas à repérer les coordonnées du point C ainsi

\hspace{0.6cm} x_{C} y_{C}

C(-1;-2)

Je calcule l’ordonnée à l’origine, en utilisant la formule suivante ( ici, c’est : C qui est le point de la droite d )

b= y_{C} – ax_{C}

On prend soin ensuite de remplacer les lettres par les bons nombres. Si le nombre est négatif, je prends l’habitude de l’écrire entre parenthèses.

b= y_{C} – ax_{C} \\b=-2-0\times(-1) \\b=-2

Pour finir je remplace a et b par 0 et -2 dans l’équation réduite y=ax+b

L’équation de la droite d est y= 0 x-2 ou y= -2  

 

d passe par C(-2;-3) et a pour coefficient directeur 1

D’après l’énoncé le coefficient directeur a=1

On n’hésite pas à repérer les coordonnées du point C ainsi

\hspace{0.6cm} x_{C} y_{C}

C(-2;-3)

Je calcule l’ordonnée à l’origine, en utilisant la formule suivante ( ici, c’est : C qui est le point de la droite d )

b= y_{C} – ax_{C}

On prend soin ensuite de remplacer les lettres par les bons nombres. Si le nombre est négatif, je prends l’habitude de l’écrire entre parenthèses.

b= y_{C} – ax_{C} \\b=-3-1\times(-2) \\b=-3+2\\b=-1

Pour finir je remplace a et b par 1 et -1 dans l’équation réduite y=ax+b

L’équation de la droite d est y= 1 x-1 ou y= x-1  

 

 

d passe par E(-1;0) et est parallèle à la droite d’équation réduite y=x-3

On désigne par a le coefficient directeur de la droite d .

Le coefficient directeur de la droite d’équation y=x-3 vaut 1.

Comme les droites sont parallèles, leurs coefficients directeurs sont égaux donc a=1

On n’hésite pas à repérer les coordonnées du point E ainsi

\hspace{0.5cm} x_{E} y_{E}

E(-1;0)

Je calcule l’ordonnée à l’origine, en utilisant la formule suivante ( ici, c’est : E qui est le point de la droite d )

b= y_{E} – ax_{E}

On prend soin ensuite de remplacer les lettres par les bons nombres. Si le nombre est négatif, je prends l’habitude de l’écrire entre parenthèses.

b= y_{E} – ax_{E} \\b=0-1\times(-1) \\b=0+1 \\b=1

Pour finir je remplace a et b par 1 et 1 dans l’équation réduite y=ax+b

L’équation de la droite d est

y= 1x+1 \\y= x+1

 

 

d passe par E(0;\frac{1}{2}) et est parallèle à la droite d’équation réduite y=-2x+1

On désigne par a le coefficient directeur de la droite d .

Le coefficient directeur de la droite d’équation y=-2x+1 vaut -2 .

Comme les droites sont parallèles, leurs coefficients directeurs sont égaux donc a=-2

On n’hésite pas à repérer les coordonnées du point E ainsi

\hspace{0.3cm} x_{E} y_{E}

E(0;\frac{1}{2})

Je calcule l’ordonnée à l’origine, en utilisant la formule suivante ( ici, c’est : E qui est le point de la droite d )

b= y_{E} – ax_{E}

On prend soin ensuite de remplacer les lettres par les bons nombres. Si le nombre est négatif, je prends l’habitude de l’écrire entre parenthèses.

b= y_{E} – ax_{E} \\b=\frac{1}{2}-(-2)\times 0\\b=\frac{1}{2}+0 \\b=\frac{1}{2}

Pour finir je remplace a et b par -2 et \frac{1}{2} dans l’équation réduite y=ax+b

L’équation de la droite d est y= -2x+\frac{1}{2}

 

 

d passe par E(-\frac{1}{2};2) et est parallèle à la droite d’équation réduite y=3

On désigne par a le coefficient directeur de la droite d .

Le coefficient directeur de la droite d’équation y=3 vaut 0 .

Comme les droites sont parallèles, leurs coefficients directeurs sont égaux donc a=0

On n’hésite pas à repérer les coordonnées du point E ainsi

\hspace{0.5cm} x_{E} y_{E}

E(-\frac{1}{2};2)

Je calcule l’ordonnée à l’origine, en utilisant la formule suivante ( ici, c’est : E qui est le point de la droite d )

b= y_{E} – ax_{E}

On prend soin ensuite de remplacer les lettres par les bons nombres. Si le nombre est négatif, je prends l’habitude de l’écrire entre parenthèses.

b= y_{E} – ax_{E} \\b=2-0\times{(-\frac{1}{2})}\\b=2-0 \\b=2

Pour finir je remplace a et b par 0 et 2 dans l’équation réduite y=ax+b

L’équation de la droite d est y= 0x+2 ou y= 2

 

 

d passe par E(1;1) et est parallèle à la droite d’équation réduite y=-\frac{1}{2}x+2

On désigne par a le coefficient directeur de la droite d .

Le coefficient directeur de la droite d’équation y=-\frac{1}{2}x+2 vaut -\frac{1}{2} .

Comme les droites sont parallèles, leurs coefficients directeurs sont égaux donc a=-\frac{1}{2}

On n’hésite pas à repérer les coordonnées du point E ainsi

\hspace{0.5cm} x_{E} y_{E}

E(1;1)

Je calcule l’ordonnée à l’origine, en utilisant la formule suivante ( ici, c’est : E qui est le point de la droite d )

b= y_{E} – ax_{E}

On prend soin ensuite de remplacer les lettres par les bons nombres. Si le nombre est négatif, je prends l’habitude de l’écrire entre parenthèses.

b= y_{E} – ax_{E} \\b=1-{(-\frac{1}{2})}\times{1}\\b=1+ \frac{1}{2} \\b=\frac{2}{2}+ \frac{1}{2}\\b=\frac{3}{2}

Pour finir je remplace a et b par -\frac{1}{2} et \frac{3}{2} dans l’équation réduite y=ax+b

L’équation de la droite d est y= -\frac{1}{2}x+\frac{3}{2}  

 

 

d passe par E(-2;-3) et est parallèle à la droite d’équation réduite y=\frac{2}{3}x-1

On désigne par a le coefficient directeur de la droite d .

Le coefficient directeur de la droite d’équation y=\frac{2}{3}x-1 vaut \frac{2}{3} .

Comme les droites sont parallèles, leurs coefficients directeurs sont égaux donc a=\frac{2}{3}

On n’hésite pas à repérer les coordonnées du point E ainsi

\hspace{0.6cm} x_{E} y_{E}

E(-2;-3)

Je calcule l’ordonnée à l’origine, en utilisant la formule suivante ( ici, c’est : E qui est le point de la droite d )

b= y_{E} – ax_{E}

On prend soin ensuite de remplacer les lettres par les bons nombres. Si le nombre est négatif, je prends l’habitude de l’écrire entre parenthèses.

b= y_{E} – ax_{E} \\b=(-3)-{(\frac{2}{3})}\times{(-2)}\\b=-3+ \frac{4}{3} \\b=-\frac{9}{3}+ \frac{4}{3}\\b=-\frac{5}{3}

Pour finir je remplace a et b par \frac{2}{3} et -\frac{5}{3} dans l’équation réduite y=ax+b

L’équation de la droite d est y= \frac{2}{3}x-\frac{5}{3}  

 

 

d passe par E(-2;-1) et a pour ordonnée à l’origine 3

Donc b=3

On n’hésite pas à repérer les coordonnées du point E ainsi

\hspace{0.6cm} x_{E} y_{E}

E(-2;-1)

Je détermine le coefficient directeur, en utilisant la formule suivante ( ici, c’est : E qui est le point de la droite d )

y_{E}= ax_{E}+b

On prend soin ensuite de remplacer les lettres par les bons nombres. Si le nombre est négatif, je prends l’habitude de l’écrire entre parenthèses.

-1=  a\times (-2)+3

L’égalité A=B peut aussi s’écrire B=A.

-2a+3= -1 \\-2a= -1-3 \\-2a= -4\\a=\frac{-4}{-2}\\a=2

Pour finir je remplace a et b par 2 et 3 dans l’équation réduite y=ax+b

L’équation de la droite d est y= 2x+3 

 

d passe par E(-2;-1) et  b=3.

Comme b=3 la droite coupe l’axe des ordonnées au  point de coordonnées (0;3). Appelons-le F.

Déterminons maintenant l’équation de la droite (EF).

On n’hésite pas à repérer les coordonnées des points E et F ainsi

\hspace{0.55cm} x_{E} y_{E} \hspace{0.8cm} x_{F} y_{F}

E(-2;-1) \hspace{0.4cm} F(0;3)

Je compare x_{E} et x_{F}

x_{E} \neq x_{F} car -2 \neq 0

Je peux donc calculer le coefficient directeur , en utilisant la formule suivante:

a=\frac{y_{F}-y_{E}} {x_{F}-x_{E}}

On prend soin ensuite de remplacer les lettres par les bons nombres. Si le nombre est négatif, je prends l’habitude de l’écrire entre parenthèses.

a=\frac{3-(-1)} {0-(-2))} \\a=\frac{4} {2}\\a=2

Pour finir je remplace a et b par 2 et 3 dans l’équation réduite y=ax+b

L’équation de la droite d est y= 2x+ 3.

 

 

 

d passe par E(\frac{1}{2};3) et a pour ordonnée à l’origine 2

Donc b=2

On n’hésite pas à repérer les coordonnées du point E ainsi

\hspace{0.3cm} x_{E} y_{E}

E(\frac{1}{2};3)

Je détermine le coefficient directeur, en utilisant la formule suivante ( ici, c’est : E qui est le point de la droite d )

y_{E}= ax_{E}+b

On prend soin ensuite de remplacer les lettres par les bons nombres. Si le nombre est négatif, je prends l’habitude de l’écrire entre parenthèses.

3=  a\times (\frac{1}{2})+2

L’égalité A=B peut aussi s’écrire B=A.

\frac{1}{2}a+2=3 \\\frac{1}{2}a= 3-2 \\\frac{1}{2}a= 1 \\a=1 \times 2\\a=2

Pour finir je remplace a et b par 2 et 2 dans l’équation réduite y=ax+b

L’équation de la droite d est y= 2x+2 

 

d passe par E(\frac{1}{2};3) et  b=2.

Comme b=2 la droite coupe l’axe des ordonnées au  point de coordonnées (0;2). Appelons-le F.

Déterminons maintenant l’équation de la droite (EF).

On n’hésite pas à repérer les coordonnées des points E et F ainsi

\hspace{0.3cm} x_{E} y_{E} \hspace{0.6cm} x_{F} y_{F}

E(\frac{1}{2};3) \hspace{0.4cm} F(0;2)

Je compare x_{E} et x_{F}

x_{E} \neq x_{F} car \frac{1}{2} \neq 0

Je peux donc calculer le coefficient directeur , en utilisant la formule suivante:

a=\frac{y_{F}-y_{E}} {x_{F}-x_{E}}

On prend soin ensuite de remplacer les lettres par les bons nombres. Si le nombre est négatif, je prends l’habitude de l’écrire entre parenthèses.

a=\frac{2-3} {0-(\frac{1}{2}))} \\a=\frac{-1}{-\frac{1}{2}}\\a=-1\times (- \frac{2}{1}) \\a=2

Pour finir je remplace a et b par 2 et 2 dans l’équation réduite y=ax+b

L’équation de la droite d est y= 2x+ 2.

 

 

 

d passe par E(6;-1) et a pour ordonnée à l’origine -1

Donc b=-1

On n’hésite pas à repérer les coordonnées du point E ainsi

\hspace{0.4cm} x_{E} y_{E}

E(6;-1)

Je détermine le coefficient directeur, en utilisant la formule suivante ( ici, c’est : E qui est le point de la droite d )

y_{E}= ax_{E}+b

On prend soin ensuite de remplacer les lettres par les bons nombres. Si le nombre est négatif, je prends l’habitude de l’écrire entre parenthèses.

(-1)=  a\times 6-1

L’égalité A=B peut aussi s’écrire B=A.

6a-1= -1 \\6a= -1+1 \\6a= 0\\a=\frac{0}{6}\\a=0

Pour finir je remplace a et b par 0 et -1 dans l’équation réduite y=ax+b

L’équation de la droite d est y= 0x-1 ou y= -1

 

 

d passe par E(6;-1) et  b=-1.

Comme b=-1 la droite coupe l’axe des ordonnées au  point de coordonnées (0;-1). Appelons-le F.

Déterminons maintenant l’équation de la droite (EF).

On n’hésite pas à repérer les coordonnées des points E et F ainsi

\hspace{0.3cm} x_{E} y_{E} \hspace{0.8cm} x_{F} y_{F}

E(6;-1) \hspace{0.4cm} F(0;-1)

Je compare x_{E} et x_{F}

x_{E} \neq x_{F} car 6 \neq 0

Je peux donc calculer le coefficient directeur , en utilisant la formule suivante:

a=\frac{y_{F}-y_{E}} {x_{F}-x_{E}}

On prend soin ensuite de remplacer les lettres par les bons nombres. Si le nombre est négatif, je prends l’habitude de l’écrire entre parenthèses.

a=\frac{(-1)-(-1)} {0-6)} \\a=\frac{-1+1}{-6}\\a=\frac{0}{-6}\\a=0

Pour finir je remplace a et b par 0 et -1 dans l’équation réduite y=ax+b

L’équation de la droite d est y= 0x-1 ou y= -1 .

 

 

 

 

d passe par E(8;0) et a pour ordonnée à l’origine -\frac{1}{2}

Donc b=-\frac{1}{2}

On n’hésite pas à repérer les coordonnées du point E ainsi

\hspace{0.25cm} x_{E} y_{E}

E(8;0)

Je détermine le coefficient directeur, en utilisant la formule suivante ( ici, c’est : E qui est le point de la droite d )

y_{E}= ax_{E}+b

On prend soin ensuite de remplacer les lettres par les bons nombres. Si le nombre est négatif, je prends l’habitude de l’écrire entre parenthèses.

0=  a\times 8-\frac{1}{2}

L’égalité A=B peut aussi s’écrire B=A.

8a-\frac{1}{2}=0\\8a= \frac{1}{2}\\a= \frac{\frac{1}{2}}{8}

Diviser par 8 revient à multiplier par son inverse \frac{1}{8}

a= {\frac{1}{2}}\times{\frac{1}{8}}\\a= \frac{1}{16}

Pour finir je remplace a et b par \frac{1}{16} et -\frac{1}{2} dans l’équation réduite y=ax+b

L’équation de la droite d est y= \frac{1}{16}x-\frac{1}{2} 

 

d passe par E(8;0) et  b=-\frac{1}{2}.

Comme b=-\frac{1}{2} la droite coupe l’axe des ordonnées au  point de coordonnées (0;-\frac{1}{2}). Appelons-le F.

Déterminons maintenant l’équation de la droite (EF).

On n’hésite pas à repérer les coordonnées des points E et F ainsi

\hspace{0.3cm} x_{E} y_{E} \hspace{0.8cm} x_{F} y_{F}

E(8;0) \hspace{0.4cm} F(0;-\frac{1}{2})

Je compare x_{E} et x_{F}

x_{E} \neq x_{F} car 8 \neq 0

Je peux donc calculer le coefficient directeur , en utilisant la formule suivante:

a=\frac{y_{F}-y_{E}} {x_{F}-x_{E}}

On prend soin ensuite de remplacer les lettres par les bons nombres. Si le nombre est négatif, je prends l’habitude de l’écrire entre parenthèses.

a=\frac{(-\frac{1}{2})-0} {0-8} \\a=\frac{-\frac{1}{2}}{-8}\\a={-\frac{1}{2}}\times {(-\frac{1}{8})}\\a=\frac{1}{16}

Pour finir je remplace a et b par \frac{1}{16} et -\frac{1}{2} dans l’équation réduite y=ax+b

L’équation de la droite d est y= \frac{1}{16}x-\frac{1}{2}

 

 

 

d passe par E(\frac{1}{5};\frac{1}{4}) et a pour ordonnée à l’origine 0

Donc b=0

On n’hésite pas à repérer les coordonnées du point E ainsi

\hspace{0.3cm} x_{E} y_{E}

E(\frac{1}{5};\frac{1}{4})

Je détermine le coefficient directeur, en utilisant la formule suivante ( ici, c’est : E qui est le point de la droite d )

y_{E}= ax_{E}+b

On prend soin ensuite de remplacer les lettres par les bons nombres. Si le nombre est négatif, je prends l’habitude de l’écrire entre parenthèses.

\frac{1}{4}=  a\times (\frac{1}{5})+0

L’égalité A=B peut aussi s’écrire B=A.

\frac{1}{5}a=\frac{1}{4}\\a={\frac{1}{4}}\times{5}\\a=\frac{5}{4}

Pour finir je remplace a et b par \frac{5}{4} et 0 dans l’équation réduite y=ax+b

L’équation de la droite d est y= \frac{5}{4}x+0 ou y= \frac{5}{4}x

 

d passe par E(\frac{1}{5};\frac{1}{4}) et  b=0.

Comme b=0 la droite coupe l’axe des ordonnées au  point de coordonnées (0;0). Appelons-le F.

Déterminons maintenant l’équation de la droite (EF).

On n’hésite pas à repérer les coordonnées des points E et F ainsi

\hspace{0.3cm} x_{E} y_{E} \hspace{0.6cm} x_{F} y_{F}

E(\frac{1}{5};\frac{1}{4}) \hspace{0.4cm} F(0;0)

Je compare x_{E} et x_{F}

x_{E} \neq x_{F} car \frac{1}{5} \neq 0

Je peux donc calculer le coefficient directeur , en utilisant la formule suivante:

a=\frac{y_{F}-y_{E}} {x_{F}-x_{E}}

On prend soin ensuite de remplacer les lettres par les bons nombres. Si le nombre est négatif, je prends l’habitude de l’écrire entre parenthèses.

a=\frac{0-\frac{1}{4}} {0-\frac{1}{5}} \\a=\frac{-\frac{1}{4}} {-\frac{1}{5}} \\a={\frac{1}{4}}\times {\frac{5}{1}} \\a=\frac{5}{4}

Pour finir je remplace a et b par \frac{5}{4} et 0 dans l’équation réduite y=ax+b

L’équation de la droite d est y= \frac{5}{4}x+ 0 ou y= \frac{5}{4}x.

 

 

 

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.