A. Cosinus, sinus et tangente d’un angle aigu.
1.Définition:
Soit ABC un triangle rectangle en B
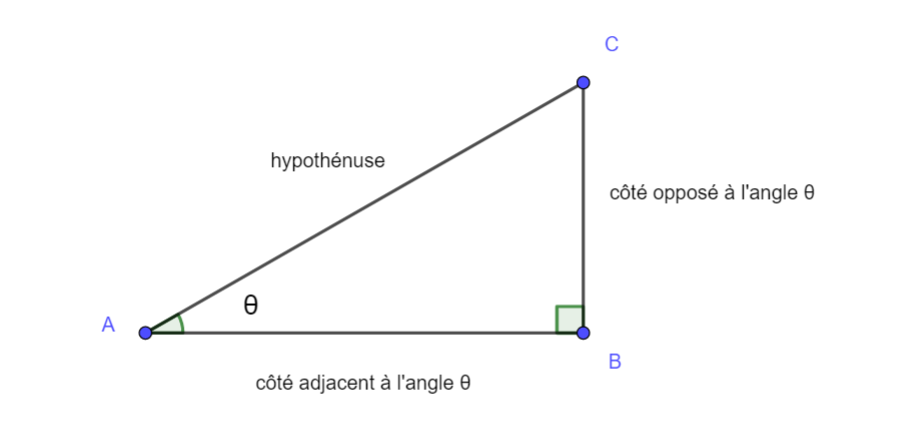
On appelle sinus de l’angle \widehat{ABC} le quotient \frac{BC}{AC}.(\frac{côté \hspace{0.1cm}opposé\hspace{0.1cm}à \hspace{0.1cm} l’angle}{hypothénuse}).
On appelle cosinus de l’angle \widehat{ABC} le quotient \frac{AB}{AC}(\frac{côté \hspace{0.1cm}adjacent\hspace{0.1cm}à \hspace{0.1cm} l’angle}{hypothénuse}).
On appelle tangente de l’angle \widehat{ABC} le quotient \frac{BC}{AB}.(\frac{côté \hspace{0.1cm}opposé\hspace{0.1cm}à \hspace{0.1cm} l’angle}{côté \hspace{0.1cm}adjacent\hspace{0.1cm}à \hspace{0.1cm} l’angle}).
On note sin(\widehat{ABC})=\frac{BC}{AC}; cos(\widehat{ABC})=\frac{AB}{AC} et tan(\widehat{ABC})=\frac{BC}{AB}
Pour s’en rappeler :
SOPHY CACHE TOA
SinOPposéHYpothéuse CosAdjaCentHypothénusE TanOpposéAdjacent
Exercice n°1:
Soit ABC un triangle rectangle en A.
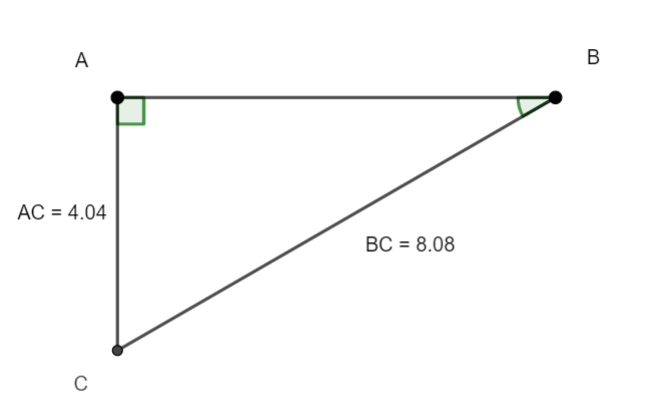
1.Dans le triangle rectangle ABC en A, quel est le côté opposé à l’angle \widehat{B} et quel côté est l’hypothénuse?
2.Déterminer sin(\widehat{B}) à l’aide de la formule de la définition.
Exercice n°2:
Soit ABC un triangle rectangle en A.
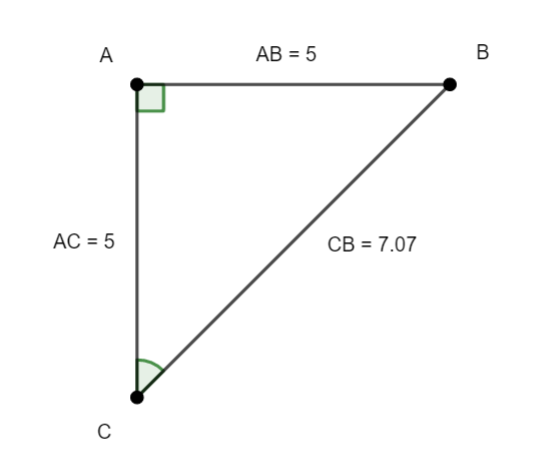
1.Dans le triangle rectangle ABC en A, quel est le côté adjacent à l’angle \widehat{C} et quel côté est l’hypothénuse?
2.Déterminer cos(\widehat{C}) à l’aide de la formule de la définition.
Exercice n°3:
Soit ABC un triangle rectangle en B.
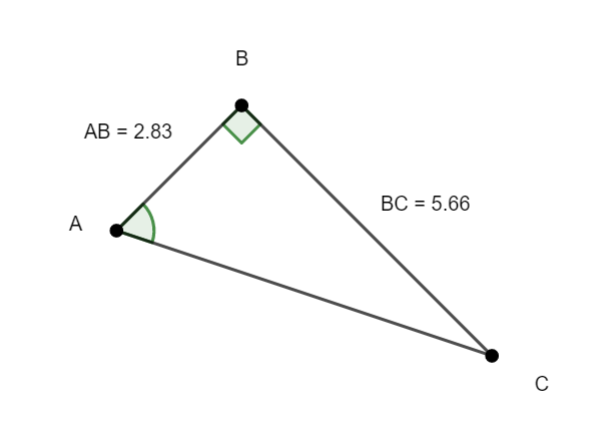
1.Dans le triangle rectangle ABC en B, quel est le côté opposé à l’angle \widehat{A} et quel est le côté adjacent à l’angle \widehat{A}?
2.Déterminer tan(\widehat{A}) à l’aide de la formule de la définition.
2. Utilisation de la calculatrice TI83 Python
On connaît la mesure de l’angle en degrés, par exemple 45° et on veut calculer cos 45°.

On connaît la valeur du cosinus par exemple 0.5 et on veut calculer la mesure de l’angle.

Exercice n°4:
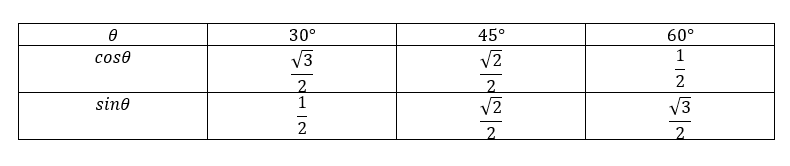
A l’aide votre calculatrice, compléter le tableau suivant.

Exercice n°5:
Soit ABC un triangle rectangle en A.
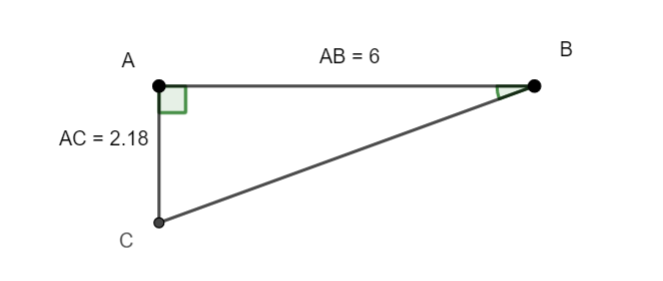
1.Déterminer tan(\widehat{B}) à l’aide de la formule de la définition.
2.En déduire la mesure en degré de l’angle \widehat{B}
B. La relation cos^2(\alpha)+sin^2(\alpha)=1où \alpha est un angle aigu.
1.Activité:
Soit AMC un triangle rectangle en C. On ne connaît que la longueur AM que l’on pourra remplacer par 1. Pour les distances AC et CM on ne les remplacera pas.
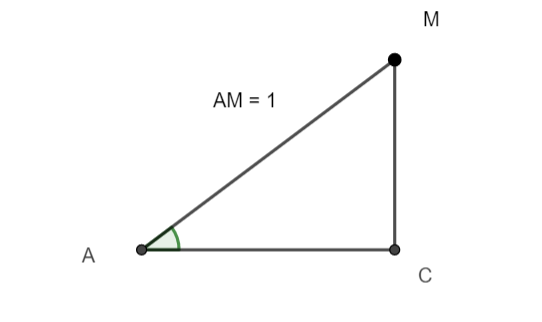
1.Déterminer sin(\widehat{A}) à l’aide de la formule de la définition.
2.Déterminer cos(\widehat{A}) à l’aide de la formule de la définition.
3.a. Appliquer le théorème de Pythagore dans le triangle AMC.
3.b. En utilisant les questions précédentes, démontrer que cos^2(\widehat{A})+sin^2(\widehat{A})=1
2.Propriété:
Pour tout angle aigu de mesure \alpha on a cos^2(\alpha)+sin^2(\alpha)=1
Exercice n°6:
On considère un angle aigu de mesure \alpha tel que sin\alpha=\frac{1}{2}. Calculer cos\alpha.
Exercice n°7:
On considère un angle aigu de mesure \alpha tel que sin\alpha=\frac{\sqrt{2}}{2}. Calculer cos\alpha.