Leopold Kronecker ( 7 décembre 1823 – 29 décembre 1891 ) est un mathématicien et logicien allemand. Il a déclaré : « Dieu a fait les nombres entiers, tout le reste est l’œuvre de l’Homme. »
1.Ensembles de nombres : définitions et propriétés:
L’ensemble des entiers naturels , noté \mathbb{N} est l’ensemble des entiers positifs ou nuls : 0; 1; 2; 3; …
L’ensemble des entiers relatifs, noté \mathbb{Z} est l’ensemble des entiers négatifs, positifs ou nuls : -3; -2; -1; 0; 1; 2; 3; …
L’ensemble des décimaux relatifs, noté \mathbb{D} est l’ensemble des nombres de la forme \frac{a}{10^n} avec a\in\mathbb{Z} et n\in\mathbb{N}
L’ensemble des rationnels, noté \mathbb{Q} est l’ensemble des nombres de la forme \frac{a}{b} avec a\in\mathbb{Z} et b\in\mathbb{N}^*
L’ensemble des réels, noté \mathbb{R} est le plus grand ensemble de nombres vu en seconde.
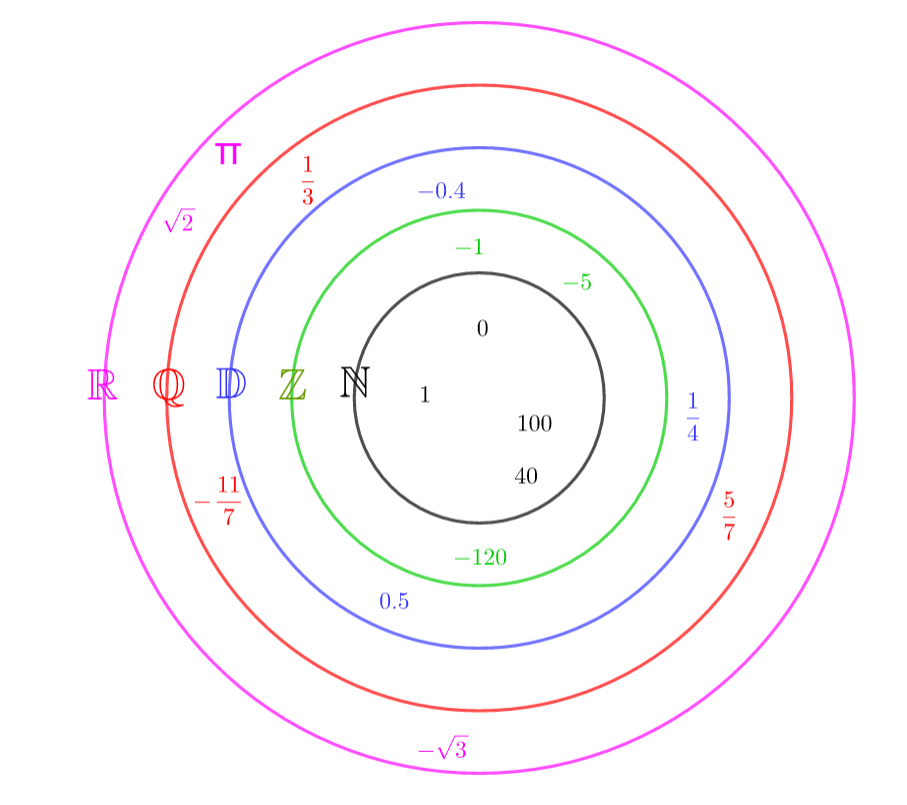
Propriété 1 :
\mathbb{N}\subset\mathbb{Z}\subset\mathbb{D}\subset\mathbb{Q}\subset\mathbb{R}Exercice n°1 :
Reproduire le tableau suivant et cocher la case quand le nombre appartient à l’ensemble.
| \mathbb{N} | \mathbb{Z} | \mathbb{D} | \mathbb{Q} | \mathbb{R} |
| 0.33 | |||||
| \frac{11}{7} | |||||
| \sqrt{14} | |||||
| \frac{\pi}{2} | |||||
| -9 | |||||
| 6 |
Exercice n°2 :
Reproduire le tableau suivant et cocher la case quand le nombre appartient à l’ensemble.
| \mathbb{N} | \mathbb{Z} | \mathbb{D} | \mathbb{Q} | \mathbb{R} |
| \frac{1}{4} | |||||
| \frac{2}{3} | |||||
| \sqrt{4} | |||||
| \frac{\pi}{5} | |||||
| 0.333 | |||||
| -6 |
2.Intervalles. Distance entre nombres réels .
a. Les intervalles
Ensemble des nombres réels x
a \leq x\leq b
On prend les valeurs comprises entre a et b ainsi que la valeur a et la valeur b.
Représentation graphique

Notation intervalle
\left[a;b\right]
Pour que la valeur a soit dans l’intervalle, on l’enferme avec un crochet fermé c’est-à-dire tourné vers l’intérieur de l’intervalle. Idem pour b.
Ensemble des nombres réels x
a \leq x< b
On prend les valeurs comprises entre a et b ainsi que la valeur a mais pas la valeur b.
Représentation graphique

Notation intervalle
\left[a;b\right[
Pour que la valeur a soit dans l’intervalle, on l’enferme avec un crochet fermé c’est-à-dire tourné vers l’intérieur de l’intervalle. Pour que b ne soit pas dans l’intervalle, on ouvre le crochet en le tournant vers l’extérieur.
Ensemble des nombres réels x
x< b
On prend les valeurs inférieures à b mais pas la valeur b.
Représentation graphique

Notation intervalle
\left]-\infty;b\right[
Du côté de -\infty, le crochet est toujours ouvert c’est-à-dire tourné vers l’extérieur de l’intervalle. Pour que b ne soit pas dans l’intervalle, on ouvre le crochet en le tournant vers l’extérieur.
Ensemble des nombres réels x
x\geq a
On prend les valeurs supérieures à a et on prend la valeur a.
Représentation graphique
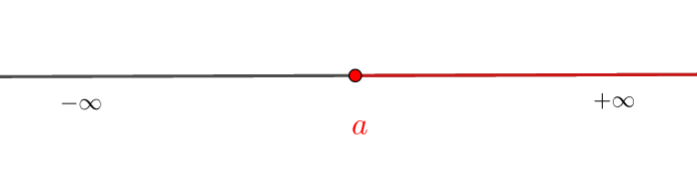
Notation intervalle
\left[a;+\infty\right[
Du côté de +\infty, le crochet est toujours ouvert c’est-à-dire tourné vers l’extérieur de l’intervalle. Pour que a soit dans l’intervalle, on ferme le crochet en le tournant vers l’intérieur.
Exercice n°3 :
Traduire chaque inégalité en utilisant la notation intervalle.
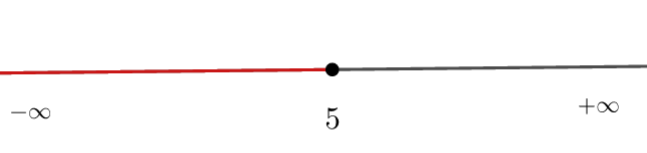
a) x<5
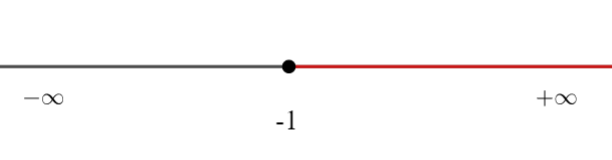
b) x>-1
c) 3<x\leq8
d) -2\leq x\leq 2
e) -6<x<6
b. Distance entre deux nombres réels
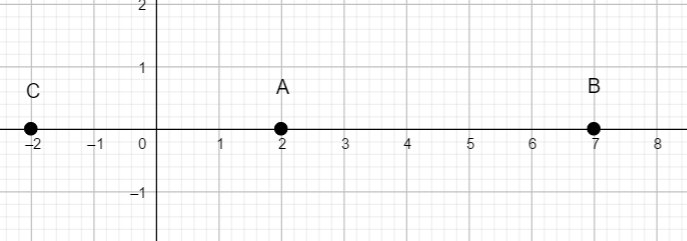
Activité n°1 : Soient les trois points A,B,C situés sur l’axe des abscisses.
Déterminer graphiquement les distances AB, BA, CA, AC, CB, BC
Synthèse de l’activité :
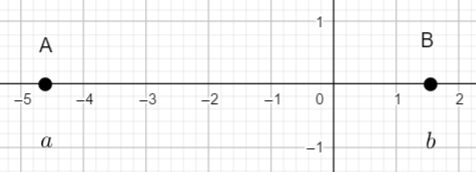
on a vu dans l’activité suivante que pour calculer la distance AB on calcule l’abscisse de B moins celle de A. Ici c’est possible car b>a et donc b-a>0.
Pour calculer la distance BA on voudrait calculer l’abscisse de A moins celle de B. Ici ce n’est pas possible car b>a
et donc a-b<0.
Pour résoudre ce problème, nous allons créer une fonction (elle s’appelle valeur absolue) qui transforme des nombres en des nombres positifs.
Définition 1 : On appelle valeur absolue d’un nombre réel x le nombre réel |x| qui vérifie :
si x\geq 0 alors |x|=x
si x\leq 0 alors |x|=-x
Exemples :
|5|=5 car 5\geq 0 ; |-3|=-(-3)=3 car -3\leq 0 ; |0.33|=0.33 car 0.33\geq 0 ; |\pi-4|=-(\pi-4)=-\pi+4 car \pi-4\leq 0
Définition 2 : Soient a et b deux nombres réels.
La distance entre les réels a et b est le nombre réel |a-b|.
Exercice n°4:
Sur la droite graduée, on a placé les points A, B, C, D d’abscisses respectives -5, -1, \frac{5}{3}, \pi.
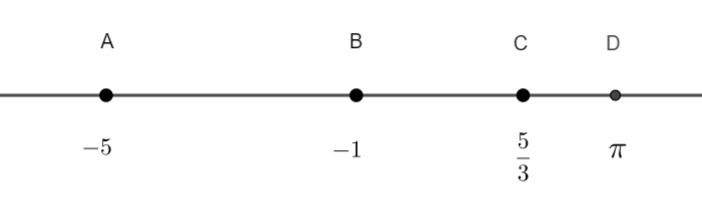
En utilisant la définition, calculer les distances AB, BD, CD, DA,CB.
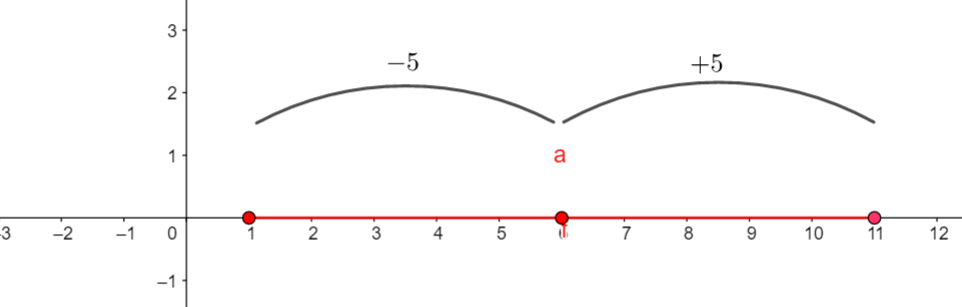
Activité n°2 : Déplacer t de telle sorte que la distance entre les réels a et t reste inférieure ou égale à 5.
A quel intervalle t appartient-il ?
Propriété 2:
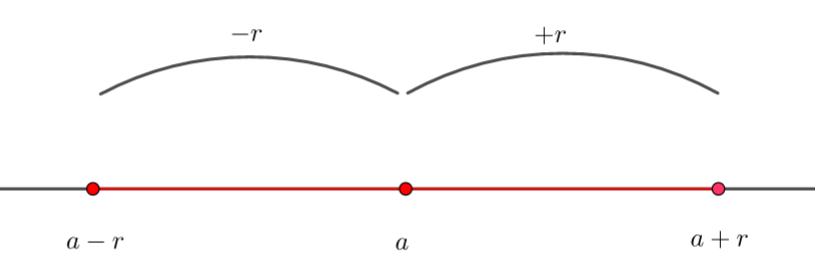
a et r désignent deux nombres réels et r>0 .
|x-a|\leq r équivaut à x\in\left[a-r;a+r\right] .
Exercice n°5:
Ecrire une inégalité vérifiée par x dans les cas suivants :