Sommaire
Multiplier deux fractions
exemple n°1: Calculer {\frac{12}{35}}\times{\frac{14}{11}}.
On applique la règle de calcul suivante : {\frac{a}{b}}\times{\frac{c}{d}}=\frac{a \times c}{b \times d}.
{\frac{12}{35}}\times{\frac{14}{11}}=\frac{12\times 14}{35\times11}
Avant de multiplier, on regarde si on peut simplifier. Ici on peut simplifier par 7 car 14=7 \times 2 et 35=7 \times 5 .
{\frac{12}{35}}\times{\frac{14}{11}}=\frac{12\times 7 \times 2}{7 \times 5\times11} \\\hspace{1.2 cm}=\frac{12\times 2}{5\times11} \\\hspace{1.2 cm}=\frac{24}{55}
exemple n°2: Calculer {\frac{3}{2}}\times{(-\frac{5}{8})}.
On applique la règle de calcul suivante : {\frac{a}{b}}\times{\frac{c}{d}}=\frac{a \times c}{b \times d}.
{\frac{3}{2}}\times{(-\frac{5}{8})}=-\frac{3\times 5}{2\times 8}
Avant de multiplier, on regarde si on peut simplifier. Ici on ne peut pas simplifier.
\hspace{1.2 cm}=-\frac{3\times 5}{2\times8} \\\hspace{1.2 cm}=-\frac{15}{16}
Validation n°1 : A l’aide de la fenêtre Géogébra ci-dessous, saisir sur la ligne n°1 le calcul à effectuer, exemple {\frac{12}{35}}\times{\frac{14}{11}} puis cliquer sur le premier onglet en haut à gauche symbolisé par le signe égal.
Validation n°2 : A l’aide de la calculatrice TI 83 Premium CE EDITION PYTHON
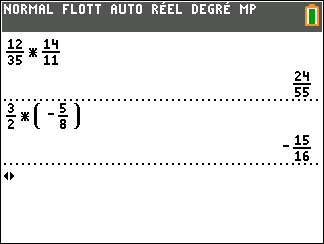
Exercice n°1: Calculer les produits suivants ( après avoir fini le calcul, penser à valider avec la page Géogébra au-dessus ou avec la calculatrice)
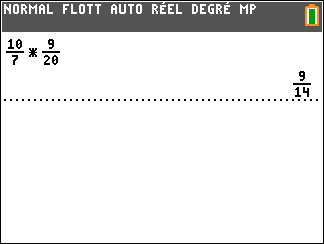
A={\frac{10}{7}}\times{\frac{9}{20}}.
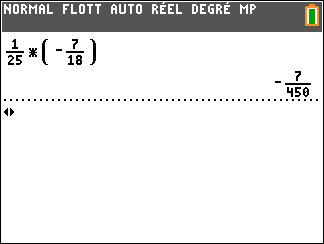
B={\frac{1}{25}}\times{(-\frac{7}{18})}.
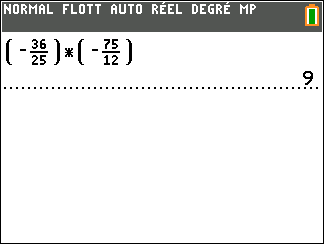
C={(-\frac{36}{25})}\times{(-\frac{75}{12})}.
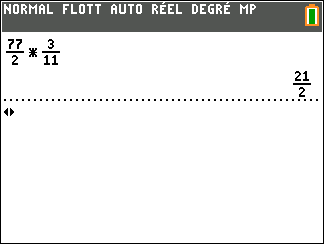
D={\frac{77}{2}}\times{\frac{3}{11}}.
Diviser deux fractions
exemple n°1: Calculer \frac{\frac{2}{7}}{\frac{6}{5}}.
On applique la règle de calcul suivante : \frac{\frac{a}{b}}{\frac{c}{d}}={\frac{a}{b}}\times{\frac{d}{c}}=\frac{a \times d}{b \times c}.
On dit aussi, diviser par une fraction revient à multiplier par son inverse.
\frac{\frac{2}{7}}{\frac{6}{5}}={\frac{2}{7}}\times{\frac{5}{6}}\\\hspace{0.4 cm}=\frac{2\times 5}{7\times 6}
Avant de multiplier, on regarde si on peut simplifier. Ici on peut simplifier par 2 car 2=2 \times 1 et 6=2 \times 3 .
\hspace{0.4 cm}=\frac{2 \times 1\times 5}{7\times 2 \times 3} \\\hspace{0.4 cm}=\frac{1\times 5}{7\times 3} \\\hspace{0.4 cm}=\frac{5}{21}
exemple n°2: Calculer \frac{\frac{11}{7}}{\frac{2}{3}}.
On applique la règle de calcul suivante : \frac{\frac{a}{b}}{\frac{c}{d}}={\frac{a}{b}}\times{\frac{d}{c}}=\frac{a \times d}{b \times c}.
On dit aussi, diviser par une fraction revient à multiplier par son inverse.
\frac{\frac{11}{7}}{\frac{2}{3}}={\frac{11}{7}}\times{\frac{3}{2}}\\\hspace{0.4 cm}=\frac{11\times 3}{7\times 2}
Avant de multiplier, on regarde si on peut simplifier. Ici on ne peut pas simplifier . .
\hspace{0.4 cm}=\frac{33}{14}
Validation n°1 : A l’aide de la fenêtre Géogébra ci-dessous, saisir sur la ligne n°1 le calcul à effectuer, exemple \frac{\frac{2}{7}}{\frac{6}{5}} puis cliquer sur le premier onglet en haut à gauche symbolisé par le signe égal.
Remarque : pour saisir le calcul, taper au clavier (2/7)/(6/5).
Validation n°2 : A l’aide de la calculatrice TI 83 Premium CE EDITION PYTHON
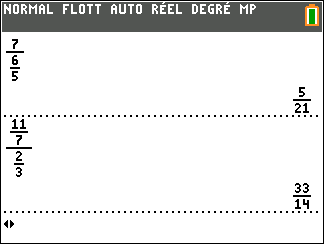
Exercice n°2: Calculer les quotients suivants ( après avoir fini le calcul, penser à valider avec la page Géogébra au-dessus ou avec la calculatrice).
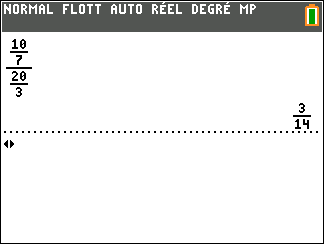
A=\frac{\frac{10}{7}}{\frac{20}{3}}.
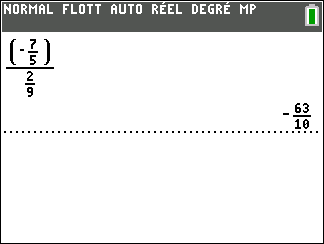
B=\frac{(-\frac{7}{5})}{\frac{2}{9}}.
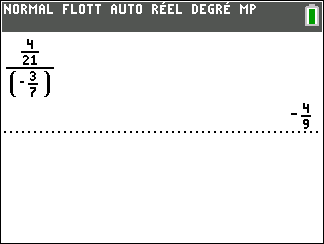
C=\frac{\frac{4}{21}}{(-\frac{3}{7})}.
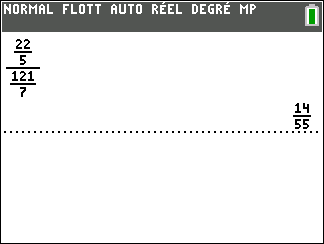
D=\frac{\frac{22}{5}}{\frac{121}{7}}.
Ajouter deux fractions
exemple n°1: Calculer \frac{5}{3}+\frac{1}{2}.
Il faut mettre au même dénominateur, ici 6.
On multiplie \frac{5}{3} par \frac{2}{2} et \frac{1}{2} par \frac{3}{3}\\\frac{5}{3}+\frac{1}{2}={\frac{5}{3}}\times{\frac{2}{2}}+{\frac{1}{2}}\times{\frac{3}{3}}\\\hspace{1 cm}=\frac{5 \times 2}{3\times 2}+\frac{1\times 3}{2\times 3}\\\hspace{1 cm}=\frac{10}{6}+\frac{3}{6}\\\hspace{1 cm}=\frac{13}{6}
exemple n°2: Calculer \frac{7}{30}-\frac{1}{15}.
Il faut mettre au même dénominateur, ici 30.
On multiplie \frac{1}{15} par \frac{2}{2} .
\frac{7}{30}-\frac{1}{15}=\frac{7}{30}-{\frac{1}{15}}\times{\frac{2}{2}}\\\hspace{1.25 cm}=\frac{7}{30}-\frac{1\times 2}{15\times 2}\\\hspace{1.25 cm}=\frac{7}{30}-\frac{2}{30}\\\hspace{1.25 cm}=\frac{5}{30}
Le résultat n’est pas une fraction irréductible, on peut simplifier par 5 .
\hspace{1.25 cm}=\frac{1}{6}
exemple n°3: Calculer -\frac{1}{30}-2.
Il faut mettre au même dénominateur, ici 30.
On multiplie 2 par \frac{30}{30} .
-\frac{1}{30}-2=-\frac{1}{30}-{2}\times{\frac{30}{30}}\\\hspace{1.25 cm}=-\frac{1}{30}-\frac{2\times 30}{30}\\\hspace{1.25 cm}=-\frac{1}{30}-\frac{60}{30}\\\hspace{1.25 cm}=-\frac{61}{30}
Validation n°1 : A l’aide de la fenêtre Géogébra ci-dessous, saisir sur la ligne n°1 le calcul à effectuer, exemple \frac{5}{3}+\frac{1}{2}puis cliquer sur le premier onglet en haut à gauche symbolisé par le signe égal.
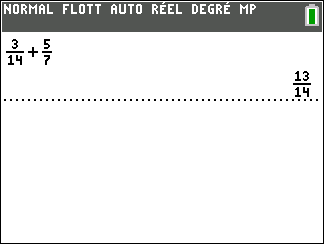
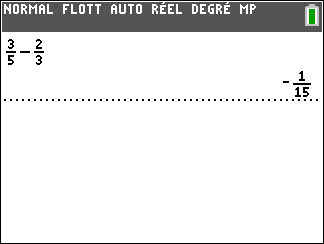
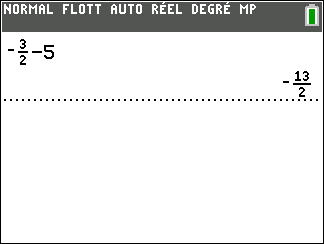
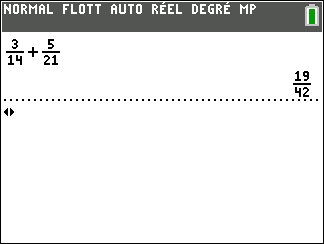
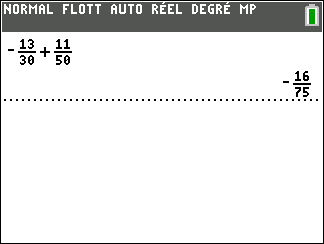
Validation n°2 : A l’aide de la calculatrice TI 83 Premium CE EDITION PYTHON
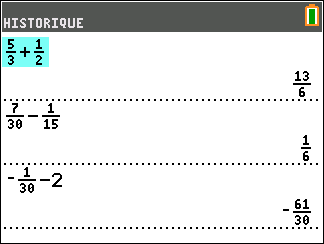
Exercice n°3: Calculer les sommes suivantes
A=\frac{3}{14}+\frac{5}{7}
B=\frac{3}{5}-\frac{2}{3}
C=-\frac{3}{2}-5
D=\frac{3}{14}+\frac{5}{21}
E=-\frac{13}{30}+\frac{11}{50}
Suites d’opérations
Dans une suite d’opérations, on effectue en priorité:
- Ce qu’il y a entre parenthèses
- Les puissances
- Les multiplications et divisions
- Les additions et soustractions
Exemple n°1 : Calculer \frac{1}{6}-{\frac{5}{3}}\times{\frac{2}{7}}
On effectue en priorité la multiplication
\frac{1}{6}-{\frac{5}{3}}\times{\frac{2}{7}}=\frac{1}{6}-\frac{5\times2}{3\times7}\\\hspace{1.6cm}=\frac{1}{6}-\frac{10}{21}
Ensuite on effectue la somme en mettant au même dénominateur, ici 42.
\hspace{1.6cm}={\frac{1}{6}}\times{\frac{7}{7}}-{\frac{10}{21}}\times{\frac{2}{2}}\\\hspace{1.6cm}=\frac{7}{42}-\frac{20}{42}\\\hspace{1.6cm}=-\frac{13}{42}
Exemple n°2 : Calculer (\frac{3}{4}+\frac{1}{2})^2+\frac{5}{3}
On effectue en priorité ce qu’il y a entre parenthèses c’est-à-dire \frac{3}{4}+\frac{1}{2}\\(\frac{3}{4}+\frac{1}{2})^2+\frac{5}{3}=(\frac{3}{4}+{\frac{1}{2}}\times{\frac{2}{2}})^2+\frac{5}{3}\\\hspace{2cm}=(\frac{3}{4}+\frac{1\times 2}{2\times 2})^2+\frac{5}{3}\\\hspace{2cm}=(\frac{3}{4}+\frac{2}{4})^2+\frac{5}{3}\\\hspace{2cm}=(\frac{5}{4})^2+\frac{5}{3}
Ensuite on effectue la puissance 2.
\hspace{2cm}=\frac{5^2}{4^2}+\frac{5}{3}\\\hspace{2cm}=\frac{25}{16}+\frac{5}{3}
Enfin on effectue la somme en mettant au même dénominateur, ici 48.
\hspace{2cm}={\frac{25}{16}}\times{\frac{3}{3}}+{\frac{5}{3}}\times{\frac{16}{16}}\\\hspace{2cm}=\frac{25\times3}{16\times3}+\frac{5\times16}{3\times16}\\\hspace{2cm}=\frac{75}{48}+\frac{80}{48}\\\hspace{2cm}=\frac{155}{48}
Validation n°1 : A l’aide de la fenêtre Géogébra ci-dessous, saisir sur la ligne n°1 le calcul à effectuer, exemple \frac{1}{6}-{\frac{5}{3}}\times{\frac{2}{7}}puis cliquer sur le premier onglet en haut à gauche symbolisé par le signe égal.
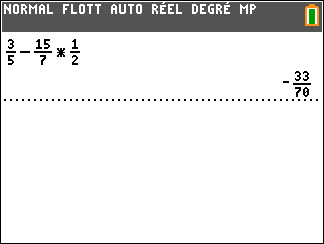
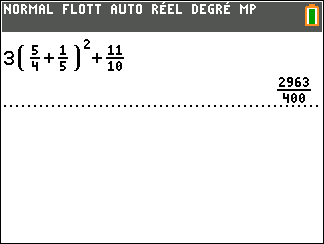
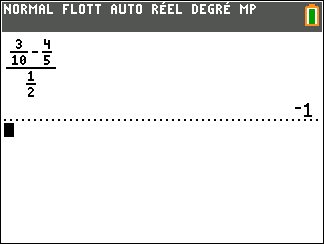
Validation n°2 : A l’aide de la calculatrice TI 83 Premium CE EDITION PYTHON
Exercice n°4: Calculer les expressions suivantes en respectant la priorité des opérations.
A=\frac{3}{5}-{\frac{15}{7}}\times{\frac{1}{2}}
B=(\frac{3}{8}+\frac{1}{4})^2+\frac{5}{4}
C=3(\frac{5}{4}+\frac{1}{5})^2+\frac{11}{10}
D=\frac{\frac{3}{10}-\frac{4}{5}}{\frac{1}{2}}