logo

2. Calculer avec des racines carrées (Rappels)

Sommaire

Un nombre est divisible par 2 s’il finit par 0, 2, 4, 6 ou 8.

Un nombre est divisible par 3 si la somme de ses chiffres est divisible par 3.

Un nombre est divisible par 5 s’il finit par 0 ou 5.

 Calcul de quelques racines carrées

Définition : Soit a un nombre réel positif. La racine carrée du nombre a est l’unique nombre réel positif dont le carré est égal à a. Pour a\geq0, (\sqrt{a})^2=a.

Attention : il faut absolument connaître au moins les carrés des onze premiers nombres entiers non nuls pour les reconnaître si besoin est. Les voici : 1; 4;9;16;25;36;49;64;81;100;121.

Exercice n°1: Calculer les racines carrées suivantes :

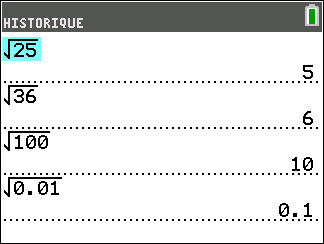
\sqrt{9}; \sqrt{25}; \sqrt{36};\sqrt{100};\sqrt{0.01}; \sqrt{0.64} .

correction

Propriété :

Pour tout réel a . Pour a\geq0, \sqrt{a^2}=|a|.

Exercice n°2: Calculer les racines carrées suivantes :

\sqrt{6^2}; \sqrt{(-2)^2}; \sqrt{(\pi-4)^2};\sqrt{(-0.1)^2};\sqrt{7^2}; \sqrt{(1-\sqrt{2})^2} .

correction

Vous pouvez valider vos réponses aux deux exercices à l’aide de la fenêtre Géogébra ci-dessous . On fait d’abord apparaître le clavier en bas à gauche.Puis cliquer sur l’icône clavier en bas à gauche de la fenêtre et d’utiliser les touches de ce clavier pour saisir par exemple \sqrt{6^2} sur la ligne 1, puis cliquer sur le premier onglet en haut à gauche.

Racine carrée d’un produit 

propriété :  Soit a et b deux nombres réels positifs. \sqrt{ab}={\sqrt a}\times{\sqrt b}

Remarque : par souci d’élégance, on écrira quand c’est possible, le résultat sous la forme a\sqrt{b}

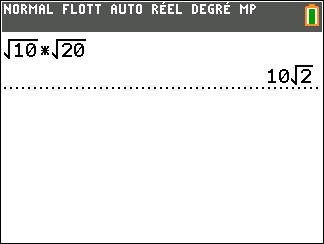
Exemple : Calculer le produit suivant {\sqrt 5}\times{\sqrt {35}} .

On applique la propriété :

{\sqrt 5}\times{\sqrt {35}}=\sqrt {5\times {35}}

Avant d’effectuer le produit, peut-on faire apparaître le carré d’un nombre ? Oui, car 35={5}\times{7}. Je remplace 35 par {5}\times{7}\\\hspace{1.6cm}=\sqrt {5\times {5}\times{7}}\\\hspace{1.6cm}=\sqrt {5^2\times{7}}\\\hspace{1.6cm}={\sqrt {5^2}}\times{\sqrt 7}\\\hspace{1.6cm}={5}\times{\sqrt 7}

On valide à l’aide de la calculatrice :

Vous pouvez valider vos réponses à l’exercice à l’aide de la fenêtre Géogébra ci-dessous . On fait d’abord apparaître le clavier en bas à gauche.Puis cliquer sur l’icône clavier en bas à gauche de la fenêtre et d’utiliser les touches de ce clavier pour saisir par exemple {\sqrt 5}\times{\sqrt {35}} sur la ligne 1, puis cliquer sur le premier onglet en haut à gauche.

Exercice n°3 : Calculer les produits suivants.

A={\sqrt 3}\times{\sqrt 6}
correction du A
B={\sqrt {15}}\times{\sqrt 7}
correction du B
C={\sqrt{ 21}}\times{\sqrt 2}
correction du C
D={\sqrt {10}}\times{\sqrt {20}}
correction du D

 Racine carrée d’un quotient

propriété :  Soit a un nombre réel positif et b un nombre réel positif non nul. \sqrt{\frac{a}{b}}=\frac{\sqrt a}{\sqrt b}

Remarque : par souci d’élégance, on écrira quand c’est possible, le résultat sous la forme a\sqrt{b}.

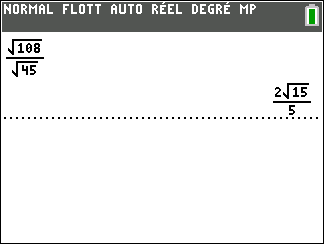
Exemple : Mettre le quotient suivant \frac{\sqrt 15}{\sqrt 6}   sous la forme \frac{\sqrt a}{b}  .

On applique la propriété :

\frac{\sqrt 15}{\sqrt 6} =\sqrt{\frac{15}{6}}

Peut-on simplifier le quotient ? Oui, car 15={3}\times{5} et  6={3}\times{2}  . Je remplace 15 par {3}\times{5} et je remplace 6 par {3}\times{2} . 

\hspace{0.7cm }=\sqrt{\frac{{3}\times{5}}{{3}\times{2}}}

On simplifie par 3.

\hspace{0.7cm } =\sqrt{\frac{5}{2}}

Puis pour faire disparaître la racine carrée du dénominateur, on multiplie par \frac{\sqrt2}{\sqrt2} .

\hspace{0.7cm } ={\sqrt{\frac{5}{2}}}\times{\frac{\sqrt2}{\sqrt2}}\\\hspace{0.7cm } ={\frac{\sqrt 5}{\sqrt 2}}\times{\frac{\sqrt 2}{\sqrt 2}}\\\hspace{0.7cm } =\frac{\sqrt{10}}{(\sqrt2)^2}\\\hspace{0.7cm } =\frac{\sqrt{10}}{2}

On valide à l’aide de la calculatrice:

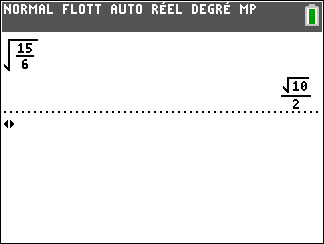
Vous pouvez valider vos réponses à l’exercice à l’aide de la fenêtre Géogébra ci-dessous . On fait d’abord apparaître le clavier en bas à gauche.Puis cliquer sur l’icône clavier en bas à gauche de la fenêtre et d’utiliser les touches de ce clavier pour saisir par exemple \frac{\sqrt 15}{\sqrt 6}  sur la ligne 1, puis cliquer sur le premier onglet en haut à gauche.

Exercice n°4 : Mettre les quotients suivants sous la forme \frac{\sqrt a}{b}.

A=\frac{\sqrt {108}}{\sqrt {45}}
correction du A
B=\frac{\sqrt {56}}{\sqrt {20}}
correction du B
C=\frac{\sqrt {35}}{\sqrt {42}}
correction du C

 Calculer en respectant la priorité des opérations

Dans une suite d’opérations, on effectue dans l’ordre :

  1. ce qu’il y a entre parenthèses
  2. les puissances
  3. les multiplications et divisions
  4. les additions et les soustractions.

Exemple : calculer 3(\sqrt2+\sqrt3)^2 +\sqrt6

1.Je ne peux calculer ce qu’il y a entre parenthèses car il n’y a pas de règle de calcul pour ajouter des racines carrées.

2. Je calcule la puissance en utilisant une identité remarquable.

a=\sqrt{2} donc a^2=\sqrt{2}^2=2

b=\sqrt{3} donc b^2=\sqrt{3}^2=3

Je calcule 2ab=2\sqrt{2}\sqrt{3}=2\sqrt{6} 

Donc (\sqrt2+\sqrt3)^2 =2+2\sqrt6+3

3(\sqrt2+\sqrt3)^2 +\sqrt6=3(2+2\sqrt6+3)+\sqrt6\\\hspace{3cm}=3(5+2\sqrt6)+\sqrt6

3. J’effectue le produit en utilisant la distributivité de la multiplication de la multiplication par rapport à l’addition.

\hspace{3cm}=3\times5+3\times2{\sqrt6}+\sqrt6\\\hspace{3cm}=15+6\sqrt6+\sqrt6

4. Je peux réduire 6\sqrt6+\sqrt6

\hspace{3cm}=15+7\sqrt6

On valide à l’aide de la calculatrice :

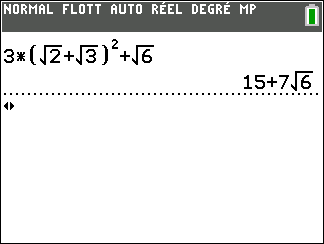
Vous pouvez valider vos réponses  à l’aide de la fenêtre Géogébra ci-dessous . On fait d’abord apparaître le clavier en bas à gauche en cliquant sur l’onglet = puis sur la ligne 1.Puis cliquer sur l’icône clavier en bas à gauche de la fenêtre et d’utiliser les touches de ce clavier pour saisir par exemple 3(\sqrt2+\sqrt3)^2 +\sqrt6 sur la ligne 1, puis cliquer sur le premier onglet en haut à gauche. 

Exercice n°5: Calculer en respectant la priorité des opérations.

A=3(1+\sqrt3)^2 +2\sqrt3-3
correction du A
B=(\sqrt3-\sqrt5)(\sqrt3+\sqrt5)
correction du B
C=3(2\sqrt6-\sqrt3)^2 +2\sqrt2+5
correction du C

©2020 – Math’O karé SAS

Nous allons utiliser la définition suivante : la racine carrée du nombre a est l’unique nombre réel positif dont le carré est égal à a.

Pour déterminer \sqrt{9}, je me demande de quel nombre 9 est le carré. C’est le carré de 3, donc 

\sqrt{9}=3.

Pour déterminer \sqrt{25}, je me demande de quel nombre 25 est le carré. C’est le carré de 5, donc 

\sqrt{25}=5.

Pour déterminer \sqrt{36}, je me demande de quel nombre 36 est le carré. C’est le carré de 6, donc 

\sqrt{36}=6

Pour déterminer \sqrt{100}, je me demande de quel nombre 100 est le carré. C’est le carré de 10, donc 

\sqrt{100}=10

Pour déterminer \sqrt{0.01}, je me demande de quel nombre 0.01 est le carré. C’est le carré de 0.1, donc 

\sqrt{0.01}=0.1

Pour déterminer \sqrt{0.64}, je me demande de quel nombre 0.64 est le carré. C’est le carré de 0.8, donc 

\sqrt{0.64}=0.8

 

Nous allons utiliser la propriété suivante :

\sqrt{a^2}=|a|

\sqrt{6^2}=|6|=6\\\sqrt{(-2)^2}=|-2|=2\\\sqrt{(\pi-4)^2}=|\pi-4|=-(\pi-4)=-\pi+4   car  \pi-4 est négatif.

\sqrt{(-0.1)^2}=|-0.1|=0.1\\\sqrt{7^2}=|7|=7\\\sqrt{(1-\sqrt{2})^2}=|1-\sqrt{2}|=-(1-\sqrt{2})=-1+\sqrt{2}    car  1-\sqrt{2} est négatif.

On valide à l’aide de la calculatrice :

Calculer le produit suivant {\sqrt 3}\times{\sqrt 6} .

On applique la propriété :

{\sqrt 3}\times{\sqrt 6}=\sqrt {3\times 6}

Avant d’effectuer le produit, peut-on faire apparaître le carré d’un nombre ? Oui, car 6={3}\times{2}. Je remplace 6 par {3}\times{2}

\hspace{1.6cm}=\sqrt {3\times {3}\times{2}}\\\hspace{1.6cm}=\sqrt {3^2\times{2}}\\\hspace{1.6cm}={\sqrt {3^2}}\times{\sqrt 2}\\\hspace{1.6cm}={3}\times{\sqrt 2}

Je valide avec la calculatrice. 

Calculer le produit suivant {\sqrt 15}\times{\sqrt 7} .

On applique la propriété :

{\sqrt 15}\times{\sqrt 7}=\sqrt {15\times 7}

Avant d’effectuer le produit, peut-on faire apparaître le carré d’un nombre ? Non.

\hspace{1.6cm}=\sqrt {105}

Je valide avec la calculatrice. 

Calculer le produit suivant {\sqrt 21}\times{\sqrt 2} .

On applique la propriété :

{\sqrt 21}\times{\sqrt 2}=\sqrt {21\times 2}

Avant d’effectuer le produit, peut-on faire apparaître le carré d’un nombre ? Non.

\hspace{1.6cm}=\sqrt {42}

Je valide avec la calculatrice. 

Calculer le produit suivant {\sqrt 10}\times{\sqrt 20} .

On applique la propriété :

{\sqrt 10}\times{\sqrt 20}=\sqrt {10\times 20}

Avant d’effectuer le produit, peut-on faire apparaître le carré d’un nombre ? Oui, car 20={10}\times{2}. Je remplace 20 par {10}\times{2}

\hspace{1.6cm}=\sqrt {10\times {10}\times{2}}\\\hspace{1.6cm}=\sqrt {10^2\times{2}}\\\hspace{1.6cm}={\sqrt {10^2}}\times{\sqrt 2}\\\hspace{1.6cm}={10}\times{\sqrt 2}

Je valide avec la calculatrice. 

Mettre le quotient suivant \frac{\sqrt 108}{\sqrt 45}   sous la forme \frac{\sqrt a}{b}  .

On applique la propriété :

\frac{\sqrt 108}{\sqrt 45} =\sqrt{\frac{108}{45}}

Peut-on simplifier le quotient ? Oui, car 108={9}\times{12} et  45={9}\times{5}  . Je remplace 108 par {9}\times{12} et je remplace 45 par {9}\times{5} . 

\hspace{0.7cm }=\sqrt{\frac{{9}\times{12}}{{9}\times{5}}}

On simplifie par 9.

\hspace{0.7cm } =\sqrt{\frac{12}{5}}

Puis pour faire disparaître la racine carrée du dénominateur, on multiplie par \frac{\sqrt5}{\sqrt5} .

\hspace{0.7cm } ={\sqrt{\frac{12}{5}}}\times{\frac{\sqrt5}{\sqrt5}}\\\hspace{0.7cm } ={\frac{\sqrt 12}{\sqrt 5}}\times{\frac{\sqrt 5}{\sqrt 5}}\\\hspace{0.7cm } =\frac{\sqrt{60}}{(\sqrt5)^2}\\\hspace{0.7cm } =\frac{\sqrt{60}}{5}

On remarque 60=4\times 15, donc :

\hspace{0.7cm } =\frac{\sqrt{4\times 15}}{5}\\\hspace{0.7cm } =\frac{{\sqrt{4}}\times {\sqrt{15}}}{5}\\\hspace{0.7cm } =\frac{2\sqrt{15}}{5}

On vérifie à l’aide de la calculatrice :

Mettre le quotient suivant \frac{\sqrt 56}{\sqrt 20}   sous la forme \frac{\sqrt a}{b}  .

On applique la propriété :

\frac{\sqrt 56}{\sqrt 20} =\sqrt{\frac{56}{20}}

Peut-on simplifier le quotient ? Oui, car 56={4}\times{14} et  20={4}\times{5}  . Je remplace 56 par {4}\times{14} et je remplace 20 par {4}\times{5} . 

\hspace{0.7cm }=\sqrt{\frac{{4}\times{14}}{{4}\times{5}}}

On simplifie par 4.

\hspace{0.7cm } =\sqrt{\frac{14}{5}}

Puis pour faire disparaître la racine carrée du dénominateur, on multiplie par \frac{\sqrt5}{\sqrt5} .

\hspace{0.7cm } ={\sqrt{\frac{14}{5}}}\times{\frac{\sqrt5}{\sqrt5}}\\\hspace{0.7cm } ={\frac{\sqrt 14}{\sqrt 5}}\times{\frac{\sqrt 5}{\sqrt 5}}\\\hspace{0.7cm } =\frac{\sqrt{70}}{(\sqrt5)^2}\\\hspace{0.7cm } =\frac{\sqrt{70}}{5}

On vérifie à l’aide de la calculatrice :

Mettre le quotient suivant \frac{\sqrt {35}}{\sqrt {42}}   sous la forme \frac{\sqrt a}{b}  .

On applique la propriété :

\frac{\sqrt {35}}{\sqrt {42}} =\sqrt{\frac{35}{42}}

Peut-on simplifier le quotient ? Oui, car 35={7}\times{5} et  42={7}\times{6}  . Je remplace 35 par {7}\times{5} et je remplace 42 par {7}\times{6} . 

\hspace{0.7cm }=\sqrt{\frac{{7}\times{5}}{{7}\times{6}}}

On simplifie par 7.

\hspace{0.7cm } =\sqrt{\frac{5}{6}}

Puis pour faire disparaître la racine carrée du dénominateur, on multiplie par \frac{\sqrt6}{\sqrt6} .

\hspace{0.7cm } ={\sqrt{\frac{5}{6}}}\times{\frac{\sqrt6}{\sqrt6}}\\\hspace{0.7cm } ={\frac{\sqrt 5}{\sqrt 6}}\times{\frac{\sqrt 6}{\sqrt 6}}\\\hspace{0.7cm } =\frac{\sqrt{30}}{(\sqrt6)^2}\\\hspace{0.7cm } =\frac{\sqrt{30}}{6}

On vérifie à l’aide de la calculatrice :

Exemple : calculer 3(1+\sqrt3)^2 +2\sqrt3-3

1.Je ne peux calculer ce qu’il y a entre parenthèses car il n’y a pas de règle de calcul pour ajouter des nombres et des racines carrées.

2. Je calcule la puissance (1+\sqrt3)^2 en utilisant une identité remarquable.

a=1 donc a^2=1^2=1

b=\sqrt{3} donc b^2=\sqrt{3}^2=3

Je calcule 2ab=2\times 1\times\sqrt{3}=2\sqrt{3} 

Donc (1+\sqrt3)^2 =1+2\sqrt3+3

3(1+\sqrt3)^2 +2\sqrt3-3=3(1+2\sqrt3+3)+2\sqrt3-3\\\hspace{3.5cm}=3(4+2\sqrt3)+2\sqrt3-3

3. J’effectue le produit en utilisant la distributivité de la multiplication de la multiplication par rapport à l’addition.

\hspace{3.5cm}=3\times4+3\times2{\sqrt3}+2\sqrt3-3\\\hspace{3.5cm}=12+6\sqrt3+2\sqrt3-3

4. Je peux réduire 6\sqrt3+2\sqrt3 et 12-3

\hspace{3.5cm}=12+8\sqrt3-3\\\hspace{3.5cm}=9+8\sqrt3

On valide à l’aide de la calculatrice :

Calculer (\sqrt3-\sqrt5)(\sqrt3+\sqrt5)

1.Je ne peux calculer ce qu’il y a entre parenthèses car il n’y a pas de règle de calcul pour ajouter  des racines carrées.

2. Il n’y a pas de puissance à calculer.

3. J’effectue le produit  en utilisant une identité remarquable.

a=\sqrt{3} donc a^2=\sqrt{3}^2=3

b=\sqrt{5} donc b^2=\sqrt{5}^2=5

Donc

(\sqrt3-\sqrt5)(\sqrt3+\sqrt5)=3-5\\\hspace{3.4cm}=-2

On valide à l’aide de la calculatrice :

Exemple : calculer 3(2\sqrt6-\sqrt3)^2 +2\sqrt2+5

1.Je ne peux calculer ce qu’il y a entre parenthèses car il n’y a pas de règle de calcul pour ajouter des nombres et des racines carrées.

2. Je calcule la puissance (2\sqrt6-\sqrt3)^2 en utilisant une identité remarquable.

a=2\sqrt6 donc a^2=(2\sqrt6)^2={2^2}\times{\sqrt6^2}=4\times6=24

b=\sqrt{3} donc b^2=\sqrt{3}^2=3

Je calcule 2ab=2\times 2\sqrt6\times\sqrt{3}=4\sqrt{6\times3}=4\sqrt{18}=4\sqrt{9\times2}=4\sqrt9\times\sqrt{2}=4\times 3\sqrt{2}=12\sqrt2 

Donc (2\sqrt6-\sqrt3)^2 =24-12\sqrt2+3

3(2\sqrt6-\sqrt3)^2 +2\sqrt2+5=3(24-12\sqrt2+3) +2\sqrt2+5

\hspace{4cm}=3(27-12\sqrt2) +2\sqrt2+5

3. J’effectue le produit en utilisant la distributivité de la multiplication de la multiplication par rapport à l’addition.

\hspace{4cm}=3\times27-3\times12{\sqrt2}+2\sqrt2+5\\\hspace{4cm}=81-36\sqrt2+2\sqrt2+5

4. Je peux réduire -36\sqrt2+2\sqrt2 et 81+5

\hspace{4cm}=86-34\sqrt2

On valide à l’aide de la calculatrice :

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.