Définition 1:
Soit une droite D et A un point du plan.
Le projeté orthogonal H de A sur la droite D est le point d’intersection de D et de la droite perpendiculaire à D passant par A.
Construction du projeté orthogonal H de A sur la droite D dans la fenêtre Géogébra ci-dessous.
- Cliquer gauche sur le 4ème onglet en haut à partir de la gauche et sélectionner Perpendiculaire dans le menu déroulant. Dans le repère cliquer gauche sur A puis sur la droite.
- Cliquer gauche sur le 2ème onglet en haut à partir de la gauche et sélectionner Intersection dans le menu déroulant. Dans le repère cliquer gauche sur la première droite et puis sur la seconde. Le logiciel nomme le nouveau point C. Pour le renommer, cliquer droit sur le point et sélectionner Renommer dans le menu déroulant puis le nommer H.
Définition 2 :
On appelle distance d’un point à une droite la plus petite distance entre ce point et un point de la droite.
Activité :
- Cliquer gauche sur le 2ème onglet en haut à partir de la gauche et sélectionner Point sur objet dans le menu déroulant. Dans le repère cliquer gauche sur la droite. Le logiciel nomme le nouveau point C. Pour le renommer, cliquer droit sur le point et sélectionner Renommer dans le menu déroulant puis le nommer M.
- Cliquer gauche sur le 8ème onglet en haut à partir de la gauche et sélectionner Distance ou longueur dans le menu déroulant. Dans le repère cliquer gauche le point A et puis sur le pointM . Le logiciel affiche la mesure de la distance AM .
- Cliquer gauche sur le 1er onglet en haut à partir de la gauche et sélectionner Déplacer dans le menu déroulant. Dans le repère déplacer le point M. Déterminer la plus petite valeur de AM qui sera la distance de A à la droite D.
Question : A quelle position de M correspond la plus petite distance.
Propriété
Soit une droite D et A un point du plan.
Soit H le projeté othogonal de A sur la droite D .
La distance du point A à la droite D est la distance AH.
Exercice n°1:
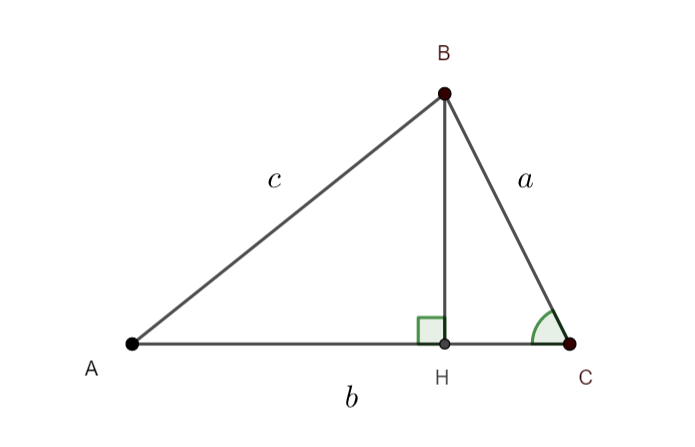
Soit ABC un triangle tel que AB=c, AC=b et BC=a.
H est le projeté orthogonal