logo

Problème n°8 : Formule d’Al-Kashi.

Soit ABC un triangle tel que AB=c, AC=b et BC=a.

H est le projeté orthogonal de B sur (AC).

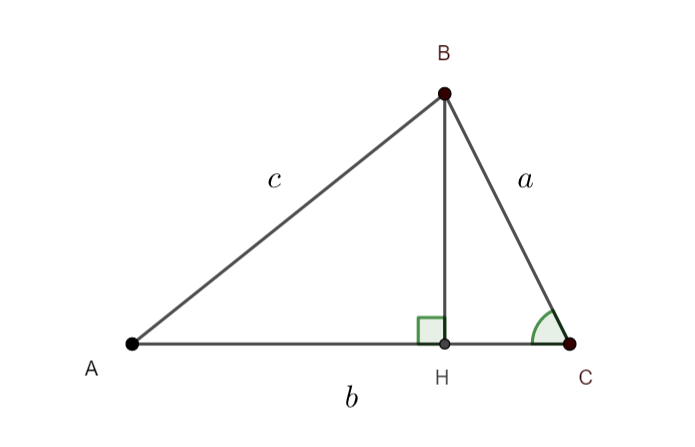
Le but du problème est d’établir l’égalité suivante :     c^2=a^2+b^2-2abcos\widehat{ACB}

  1. On se place dans le triangle rectangle BHC.

a. Compléter les pointillés dans l’égalité  cos{\widehat{ACB}}=\frac{…}{…} et dans l’égalité  sin{\widehat{ACB}}=\frac{…}{…}.

correction

b. En déduire que  CH={a}\times {cos{\widehat{ACB}}} et que BH={a}\times {sin{\widehat{ACB}}}.

correction

2. On remarque que AH=AC-CH, en utilisant l’énoncé et les résultats de la question précédente, exprimer AH en fonction de b, de a et de  cos\widehat{ACB}.

correction

3. Appliquer le théorème de Pythagore dans le triangle rectangle AHB et en déduire l’égalité suivante :

c^2=(b-acos\widehat{ACB})^2+(asin\widehat{ACB})^2
correction

4. En déduire l’égalité cherchée :c^2=a^2+b^2-2abcos\widehat{ACB}

correction

©2020 – Math’O karé SAS

On va écrire les relations trigonométriques dans le triangle rectangle BHC

Dans le triangle BHC rectangle en H,

l’hypothénuse est le côté \left[BC\right] ,

le côté adjacent à l’angle \widehat{ACB} est le côté \left[CH\right]  et

le côté opposé à l’angle \widehat{ACB} est le côté \left[BH\right].

On peut utiliser le moyen mnémotechnique suivant SOpHy CAcHe TOA.

CAcHe donne Cos=\frac{Adjacent}{Hypothénuse}

cos\widehat{ACB}=\frac{CH}{CB}, on sait que BC=a donc cos\widehat{ACB}=\frac{CH}{a}

SOpHy donneSin=\frac{Opposé}{Hypothénuse}

sin\widehat{ACB}=\frac{BH}{CB}, on sait que BC=a donc sin\widehat{ACB}=\frac{BH}{a}

 

On utilise les résultats de la question précédente.

Comme cos\widehat{ACB}=\frac{CH}{a}

On peut écrire que 

\frac{CH}{a}=cos\widehat{ACB}

On multiplie de chaque côté par a et donc :

CH=acos\widehat{ACB}

Comme sin\widehat{ACB}=\frac{BH}{a}

On peut écrire que 

\frac{BH}{a}=sin\widehat{ACB}

On multiplie de chaque côté par a et donc :

BH=asin\widehat{ACB}

 

On utilise la donnée de l’énoncé suivante : AH=AC-CH

On remplace AC par b, c’est une donnée de l’énoncé.

On remplace CH par acos\widehat{ACB}, c’est un résultat obtenu à la question 1.b.

On obtient :

AH=b-acos\widehat{ACB}.

 

Dans le triangle AHB rectangle en H , on applique le théorème de Pythagore :

AB^2=AH^2+HB^2

On remplace AB par c, c’est une donnée de l’énoncé.

On remplace AH par b-acos\widehat{ACB}, c’est un résultat obtenu à la question 2.

On remplace HB par asin\widehat{ACB}, c’est un résultat obtenu à la question 1.b.

On obtient :

c^2=(b-acos\widehat{ACB})^2+(asin\widehat{ACB})^2.

 

On veut montrer que c^2=a^2+b^2-2abcos\widehat{ACB}.

Attention : dans une démonstration, on ne peut pas utiliser ce qu’on veut démontrer (la conclusion).

Dans le cas qui nous intéresse, on sait de quoi partir : du résultat démontré dans la question précédente.

On a montré dans la question précédente que :

c^2=(b-acos\widehat{ACB})^2+(asin\widehat{ACB})^2.

On calcule d’abord les puissances : (b-acos\widehat{ACB})^2 d’abord et (asin\widehat{ACB})^2 ensuite.

1.Pour calculer (b-acos\widehat{ACB})^2 on utilise l’identité remarquable (A-B)^2=A^2-2AB+B^2.

\hspace{2cm}A=b donc A^2=b^2

\hspace{2cm}B=acos\widehat{ACB} donc B^2=(acos\widehat{ACB})^2=a^2(cos\widehat{ACB})^2=a^2cos^2\widehat{ACB}

\hspace{2cm} 2AB=2bacos\widehat{ACB})

c^2=(b^2-2abcos\widehat{ACB}+a^2cos^2\widehat{ACB})+(asin\widehat{ACB})^2.

2. pour calculer (asin\widehat{ACB})^2 , on utilise (ab)^2=a^2b^2

c^2=b^2-2abcos\widehat{ACB}+a^2cos^2\widehat{ACB}+a^2sin^2\widehat{ACB}.

Pour finir, on utilise la propriété suivante cos^2\alpha+sin^2\alpha=1.

On met d’abord a^2 en facteur dans a^2cos^2\widehat{ACB}+a^2sin^2\widehat{ACB}.

c^2=b^2-2abcos\widehat{ACB}+a^2(cos^2\widehat{ACB}+sin^2\widehat{ACB}).

c^2=b^2-2abcos\widehat{ACB}+{a^2}\times 1.

c^2=a^2+b^2-2abcos\widehat{ACB}.

 

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.