Sommaire
Echantillonnage
Exemple n°1 : On jette une pièce de monnaie et on note le résultat obtenu en lisant la face supérieure de cette pièce. Cette expérience comporte deux issues. On la renouvelle 49 fois de suite.
Voici une fenêtre Edupython où se trouve un programme qui permet de simuler l’expérience précédente.
Remarque : avec l’instruction for i in range(1,50) : la variable i prend les quarante neuf valeurs de 1 à 49.
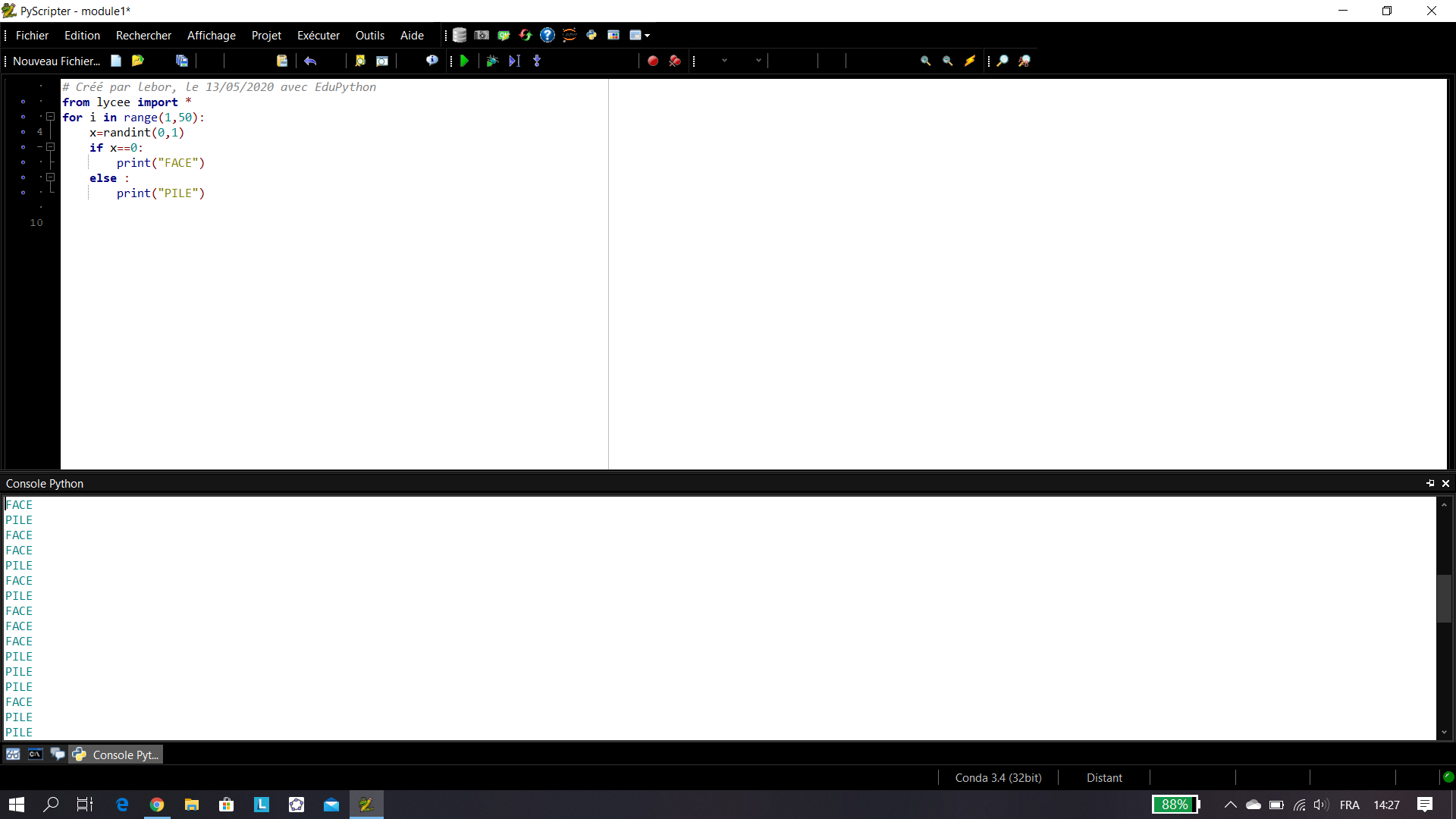
Ici on réalise plusieurs fois de suite une même expérience aléatoire à deux issues de manière indépendante ( c’est-à-dire que les résultats obtenus n’ont aucune influence entre eux ). L’ensemble des résultats obtenus FACE, PILE, FACE, FACE, PILE, FACE, PILE, FACE, FACE, FACE, PILE, PILE, PILE, FACE, PILE, PILE, … qui s’affiche dans la console est appelé échantillon. Comme on a renouvelé 49 fois l’expérience : « jeter une pièce de monnaie », on dit que l’échantillon est de taille 49.
Exemple n°2 : On jette un dé cubique équilibré et on note le résultat obtenu en lisant la face supérieure de ce dé. Cette expérience comporte six issues. On la renouvelle 19 fois de suite.
Voici une fenêtre Edupython où se trouve un programme qui permet de simuler l’expérience précédente. En exécutant ce programme, on obtient une issue possible de l’expérience.
Remarque : avec l’instruction for i in range(1,20) : la variable i prend les dix-neuf valeurs de 1 à 19.
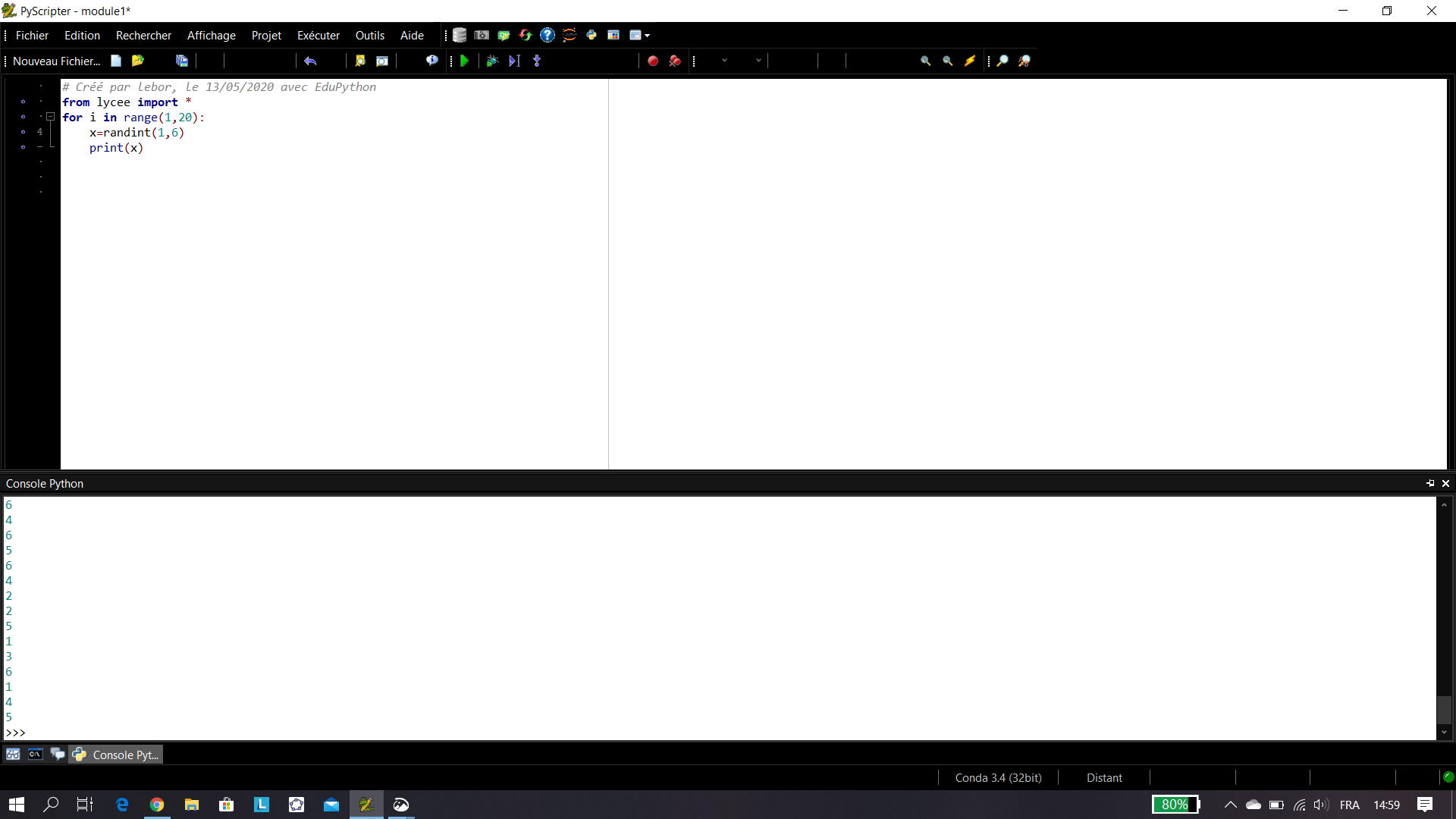
Ici on réalise plusieurs fois de suite une même expérience aléatoire à six issues de manière indépendante ( c’est-à-dire que les résultats obtenus n’ont aucune influence entre eux ). L’ensemble des résultats obtenus 6, 4, 6, 5, 6, 4, 2, 2, 5, 1, 3, 6, 1, 4, 5 ,… qui s’affiche dans la console est appelé échantillon. Comme on a renouvelé 19 fois l’expérience : « jeter un dé équilibré », on dit que l’échantillon est de taille 19.
Définition : Un échantillon de taille n est la liste des résultats obtenus en renouvelant de façon indépendante une même expérience aléatoire n fois.
Remarque : le programme officiel impose que l’expérience aléatoire qu’on renouvelle comporte uniquement deux issues. Ainsi seul l’exemple n°1 est recevable, l’exemple n°2 n’est là que pour la culture générale.
Fluctuation d’échantillonnage
Exemple n°1 : On jette une pièce de monnaie et on note le résultat obtenu en lisant la face supérieure de cette pièce. On renouvelle l’expérience 100 fois de suite. On s’intéresse à la fréquence d’apparition du caractère « obtenir PILE ».
On obtiendra des échantillons de taille 100 associés à l’expérience « jeter une pièce » dont l’une des deux issues « obtenir PILE » a pour probabilité p=\frac{1}{2}.
Voici une fenêtre Edupython où se trouve un programme qui permet de déterminer le nombre de faces obtenus (f) et le nombre de piles obtenu (p).
Remarque : avec l’instruction for i in range(100) : la variable i prend les cent valeurs de 0 à 99.
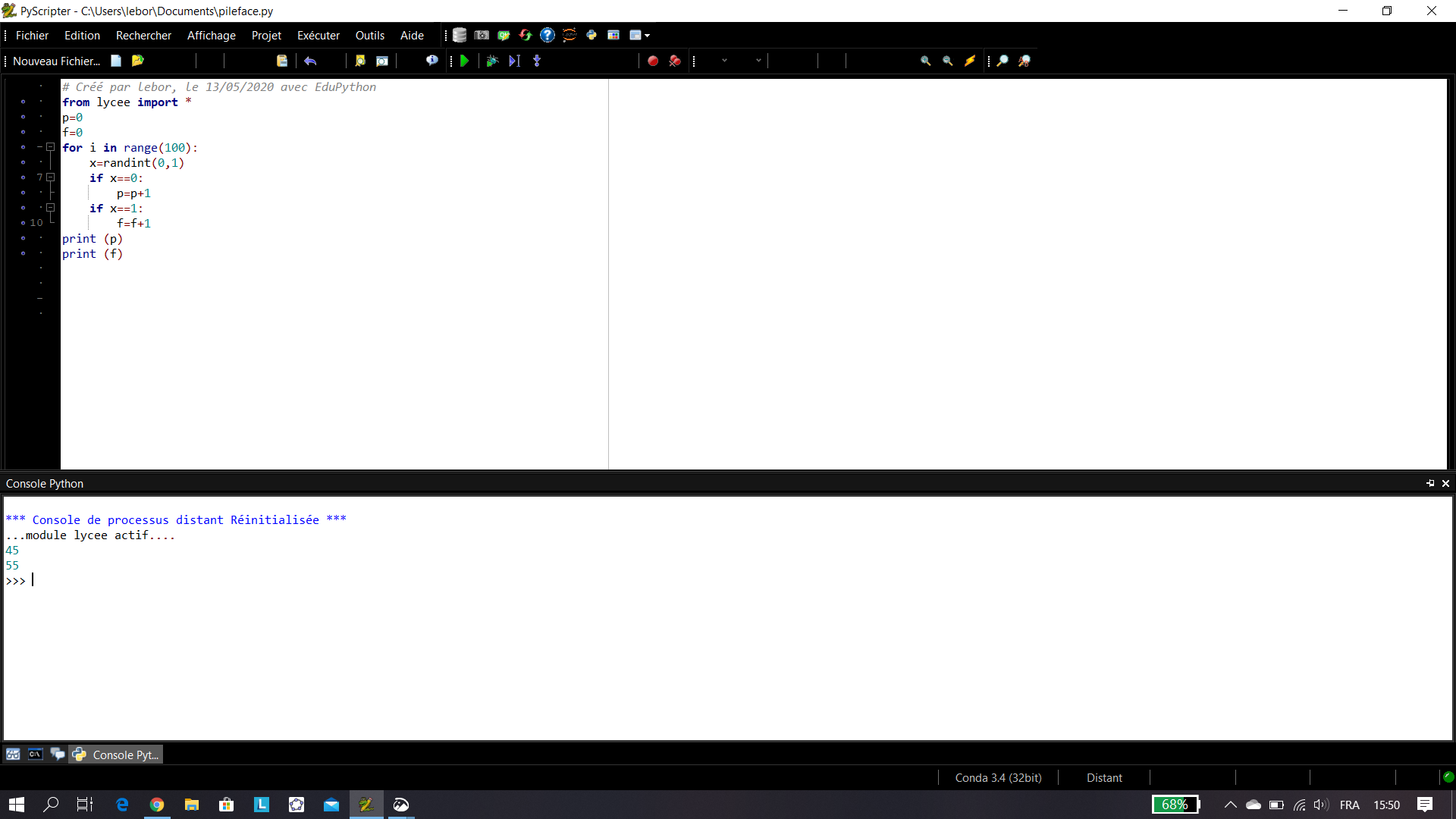
Pour notre premier échantillon :
La fréquence d’apparition de « PILE » est \frac{45}{100}=0.45.
Observons le phénomène pour d’autres échantillons :
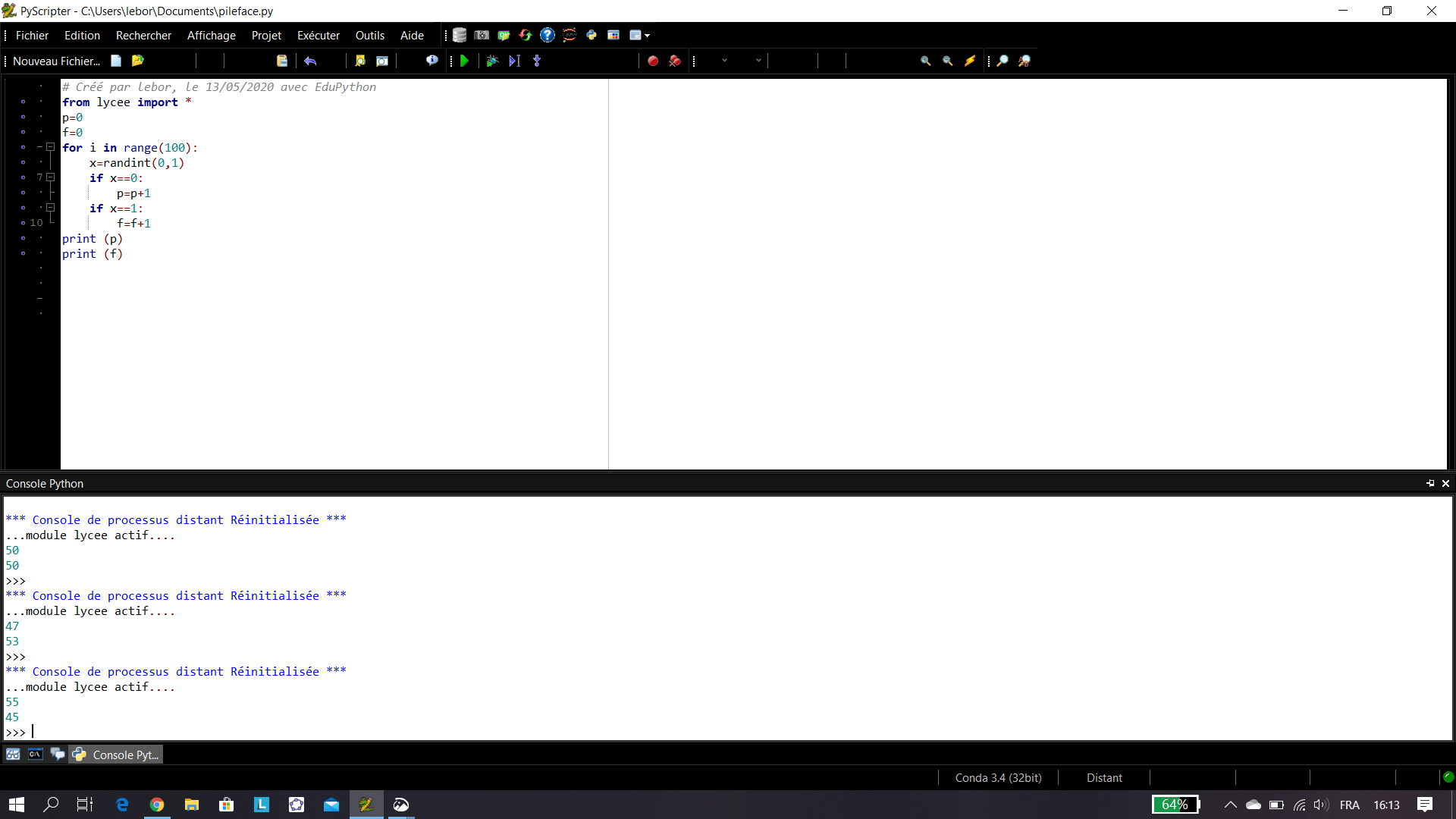
Pour le second échantillon : La fréquence d’apparition de « PILE » est \frac{50}{100}=0.5.
Pour troisième échantillon : La fréquence d’apparition de « PILE » est \frac{47}{100}=0.47.
Pour quatrième échantillon : La fréquence d’apparition de « PILE » est \frac{55}{100}=0.55.
On constate que les fréquences obtenues ne sont pas identiques mais fluctuent autour de la proportion p=\frac{1}{2}=0.5. C’est ce qu’on appelle la fluctuation d’échantillonnage.
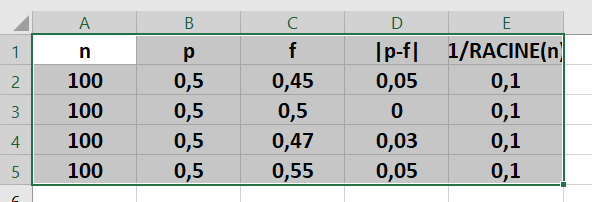
Remarque : En général, |p-f|\leq \frac{1}{\sqrt n}
C’est effectivement ce qu’on observe en comparant les résultats des deux dernières colonnes dans le tableur Excel ci-dessous.
Exemple n°2 : On tire au hasard une boule dans une urne qui contient une boule blanche et trois boules noires 40 fois de suite. On s’intéresse à la fréquence d’apparition du caractère obtenir une boule blanche.
On obtiendra des échantillons de taille 40 associés à l’expérience « tirer une boule dans l’urne » dont l’une des deux issues « obtenir une boule blanche » a pour probabilité p=\frac{1}{4}.
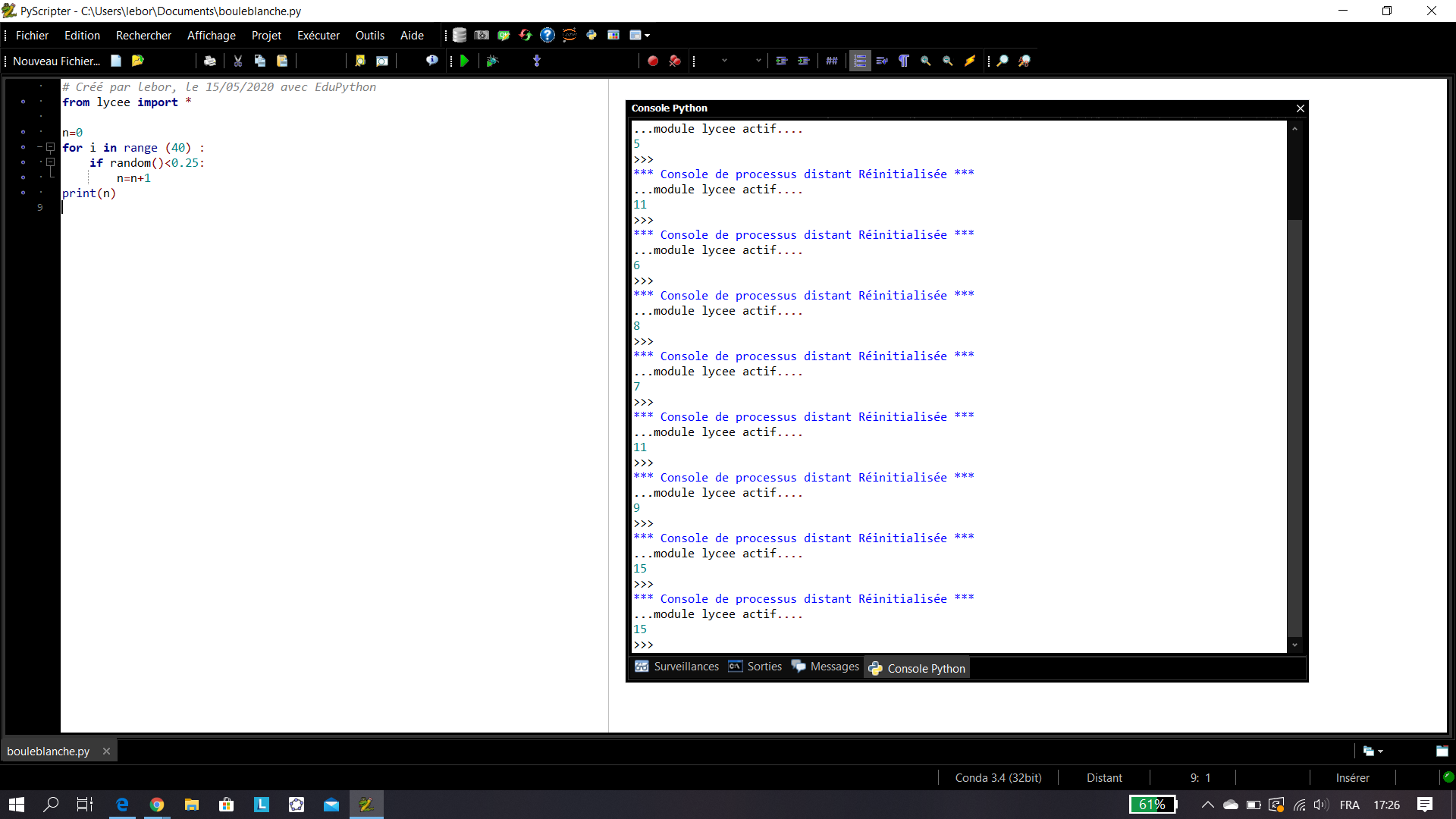
Voici une fenêtre Edupython où se trouve un programme qui permet de simuler l’expérience
Remarque : avec l’instruction for i in range(40) : la variable i prend les quarante valeurs de 0 à 39.
Pour le premier échantillon : La fréquence d’apparition de « boule blanche » est \frac{5}{40}=0.125.
Pour le second échantillon : La fréquence d’apparition de « boule blanche » est \frac{11}{40}=0.275.
Pour le troisième échantillon : La fréquence d’apparition de « boule blanche » est \frac{6}{40}=0.15.
Pour le quatrième échantillon : La fréquence d’apparition de « boule blanche » est \frac{8}{40}=0.2.
Pour le cinquième échantillon : La fréquence d’apparition de « boule blanche » est \frac{7}{40}=0.175.
Pour le sixième échantillon : La fréquence d’apparition de « boule blanche » est \frac{11}{40}=0.275.
On constate que les fréquences obtenues fluctue autour de la proportion p=\frac{1}{4}=0.25. Il s’agit de la fluctuation d’échantillonnage.
Remarque : En général, |p-f|\leq \frac{1}{\sqrt n}.
C’est effectivement ce qu’on observe en comparant les résultats des deux dernières colonnes dans le tableur Excel ci-dessous.

La loi des grands nombres
Exemple : On jette une pièce de monnaie et on note le résultat obtenu en lisant la face supérieure de cette pièce. On renouvelle cette expérience 100 fois, 1000 fois, 10000 fois, 100000 fois et 1000000 fois.
Voici les résultats obtenus en faisant varier la taille de l’échantillon:

On s’intéresse à l’évènement : « obtenir pile » dont la probabilité vaut p=\frac{1}{2}=0.5.
On constate, en observant le tableau ci-dessus, que plus la taille de l’échantillon grandit, plus les fréquences f se rapprochent de 0.5.
Propriété : Lorsque la taille de l’échantillon est grande, la fréquence observée f est proche de la proportion p.
Simulation
Exemple n°1 : On jette une pièce de monnaie et on note le résultat obtenu en lisant la face supérieure de cette pièce.
On obtiendra des échantillons de taille variable associés à l’expérience « jeter une pièce » dont l’une des deux issues « obtenir PILE » a pour probabilité p=\frac{1}{2}.
Voici les résultats obtenus en faisant varier la taille de l’échantillon:

Dans le paragraphe précédent, nous avons observé que plus la taille de l’échantillon est grande, plus la fréquence observée f est proche de la probabilité p=\frac{1}{2}, ce qui est le cas ici.
Exemple n°2:
Avant une élection, un candidat commande une enquête auprès d’un institut de sondage pour savoir quel score peut-il réaliser.
Cet institut interroge un échantillon de 1000 personnes sur leur intention de voter ou non pour ce candidat.
On obtiendra un échantillon de taille 1000 associé à l’expérience à deux issues « POUR » ou « CONTRE » . On s’intéresse à l’évènement : voter « POUR » dont on ne connaît évidemment pas la probabilité p .
Comme on ne connaît pas la probabilité d’être élu, on va utiliser ce qu’on a mis en évidence dans le paragraphe précédent, nous avons observé que plus la taille de l’échantillon est grande, plus la fréquence observée f est proche de la probabilité p.
Nous dirons que la fréquence observée est une estimation de p
Voici le résultat du sondage :
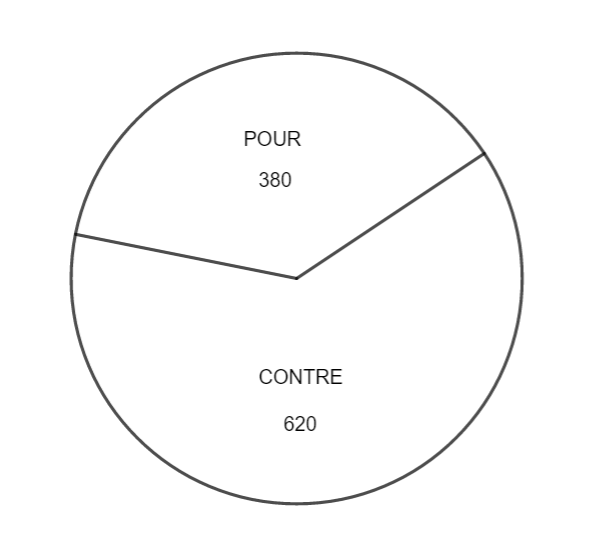
On calcule la fréquence du caractère POUR : \frac{380}{1000}=0.38 et on constate que 38% des sondés sont prêts à voter pour lui. Il est donc donné perdant.
Exemple n°3:
Une chaîne de supermarchés souhaite étudier la fréquence de paiements par carte bancaire dans ses magasins.
Il confie cette étude à un institut de sondage.
Cette étude est réalisée dans 8 magasins et on interroge un échantillon de 1000 personnes à la sortie de chaque magasin.
On obtiendra huit échantillons de taille 1000 associés à l’expérience à deux issues « paiement CB » ou « autre » . On s’intéresse à l’évènement : « paiement CB » dont on ne connaît évidemment pas la probabilité p .
Comme on ne connaît pas la probabilité de l’évènement : « paiement CB »‘, on va utiliser ce qu’on a mis en évidence dans le paragraphe précédent, nous avons observé que plus la taille de l’échantillon est grande, plus la fréquence observée f est proche de la probabilité p.
Nous dirons que la fréquence observée est une estimation de p
Voici les résultats du sondage sous forme de tableau.

On veut calculer la fréquence des paiements par CB dans chaque magasin.
Ici il n’est pas nécessaire d’utiliser la calculatrice. Pour calculer la fréquence des paiements par CB pour le magasin n°1, on divise le nombre de paiements par CB c’est-à-dire 750 par le nombre total de paiements c’est-à-dire 1000. Comme diviser par 1000 revient à déplacer la virgule de trois rangs vers la gauche, la fréquence sera égale à 0.75 ou 75 %.
Voici donc le tableau des fréquences:

On observe que les différentes fréquences fluctuent autour de 0.75.
On peut donc estimer que dans ces magasins, le pourcentage des paiements par CB est 75 %.
Propriété :
On considère un échantillon de taille n associé à une expérience aléatoire dont l’un des évènements a pour probabilité p et où f est la fréquence observée de cet évènement dans l’échantillon.
Pour n assez grand, si on ne connaît pas p on dit que f est une estimation de p.



