On veut résoudre l’équation du premier degré -3x+5=7.
1.On peut conjecturer la solution en utilisant la TI 83 Premium CE EDITION PYTHON comme indiqué ci-dessous :

2. On peut la résoudre de façon algébrique :
On veut résoudre -3x+5=7 c’est-à-dire parvenir à x=…
Dans l’équation -3x+5=7, le terme 5 n’est pas à sa place. Je dois donc enlever 5 de chaque côté.
Par al-muqabala -3x=7-5\\\hspace{1.3cm}-3x=2
Dans l’équation -3x=2, le facteur -3 n’est pas à sa place. Je dois donc diviser par -3 de chaque côté.
Par al-hatt x=-\frac{2}{3}
Donc S = \left\{-\frac{2}{3}\right\}
3. Vérification n°1: par le calcul.
Remarque: pour vérifier que votre solution est exacte, on remplace x par -\frac{2}{3} dans l’équation -3x+5=7\\{-3}\times{(-\frac{2}{3})}+5=2+5=7
L’égalité est vérifiée donc la solution trouvée convient.
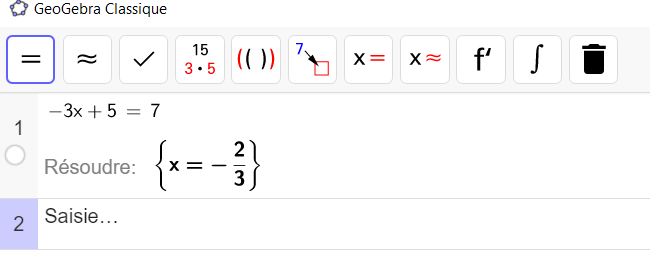
Vérification n°2: Avec l’application calcul formel de Géogébra.