Sommaire
Exercice n°1
On veut déterminer par le calcul les coordonnées de I le milieu de \left[AB\right] où \hspace{0.2cm} A(5;3) \hspace{0.4cm} B(-1;6)
On n’hésite pas à repérer les coordonnées des points A et B ainsi
\hspace{0.6cm} x_{A} y_{A} \hspace{0.6cm} x_{B} y_{B}
\hspace{0.2cm} A(5;3) \hspace{0.4cm} B(-1;6)
On écrit la formule du cours :
x_I=\frac {x_A+x_B}{2}\hspace {2cm}y_I=\frac {y_A+y_B}{2}
Et on prend soin de bien remplacer les lettres par les bons nombres. Dans le cas d’un nombre négatif, on le met entre parenthèses.
x_I=\frac {5+(-1)}{2}\hspace {2cm}y_I=\frac {3+6}{2}
On calcule. Si vous utilisez la calculatrice , tapez cette séquence de calcul (5+(-1))/2 en utilisant les parenthèses « invisibles » qui entourent le numérateur. Si vous tapez 5+(-1)/2, vous obtiendrez 4.5 car la machine calculera (-1)/2 en priorité ce qui est faux
x_I=\frac {4}{2}\hspace {2cm}y_I=\frac {9}{2}
x_I=2\hspace {2cm}y_I=\frac {9}{2}
Donc I(2;\frac {9}{2})
On peut valider la réponse avec un repère.
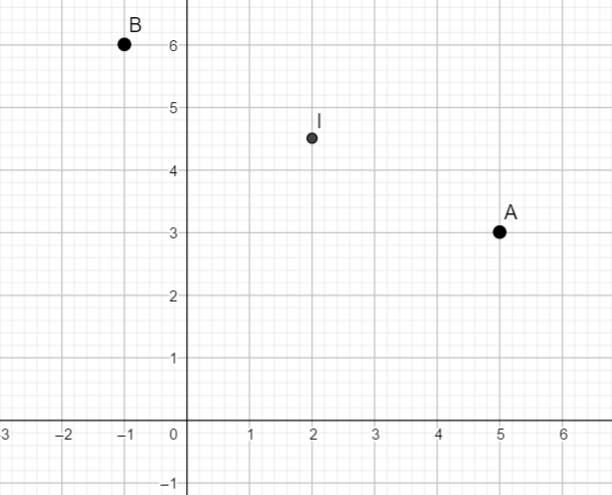
Pourquoi s’embarasser avec cette présentation ? Et bien pour pouvoir faire l’exercice suivant :
Exercice n°2
On veut déterminer par le calcul les coordonnées de D tel que I soit le milieu de [BD] où I(5;3) et B(2;4) .
Tout d’abord, on ne cherche pas les coordonnées du milieu mais celles d’un des points. Ici le point D. Comme on ne connaît pas ses coordonnées, on les remplace par les lettres x et y.
On pose D(x;y)
On n’hésite pas à repérer les coordonnées des points D , I et B ainsi
\hspace{0.4cm} x_{D} y_{D} \hspace{0.6cm} x_{I} y_{I} \hspace{0.6cm} x_{B} y_{B}
\hspace{0.2cm} D(x;y) \hspace{0.4cm} I(5;3) \hspace{0.4cm} B(2;4)
On écrit la formule du cours :
x_I=\frac {x_D+x_B}{2}\hspace {2cm}y_I=\frac {y_D+y_B}{2}Et on prend soin de bien remplacer les lettres par les bons nombres. Dans le cas d’un nombre négatif, on le met entre parenthèses.
5=\frac {x+2}{2}\hspace {2cm}3=\frac {y+4}{2}Nous avons deux équations du premier degré à résoudre. La première 5=\frac {x+2}{2} qu’on peut aussi écrire \frac {x+2}{2}=5.
Le 2 au dénominateur n’est pas à sa place, je multiplie par 2 de chaque côté de l’égalité.
x+2={5}\times{2}\\x+2=10Le 2 à gauche n’est pas à sa place, c’est un terme dans une somme. Le contraire d’ajouter 2 est enlever 2.
J’enlève 2 de chaque côté
x=10-2\\x=8La seconde 3=\frac {y+4}{2} qu’on peut aussi écrire \frac {y+4}{2}=3.
y+4={3}\times{2}\\y+4=6Le 4 à gauche n’est pas à sa place, c’est un terme dans une somme. Le contraire d’ajouter 4 est enlever 4.
J’enlève 4 de chaque côté
y=6-4\\y=2Donc D(8;2)
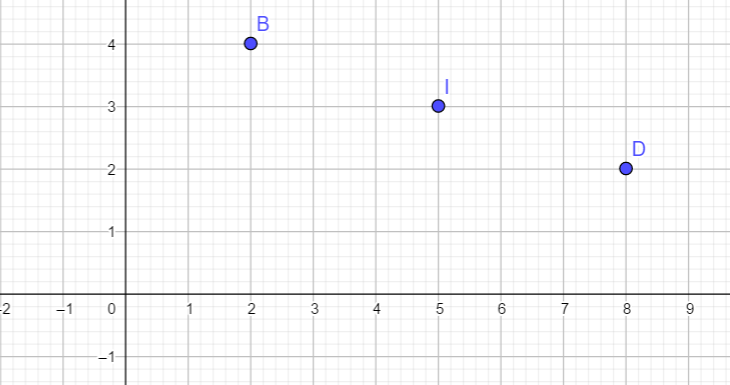
On peut valider la réponse avec un repère :