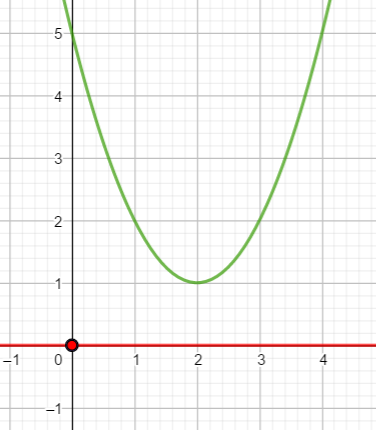
A l’aide de la représentation graphique ci-dessous déterminer, si c’est possible, le ou les antécédent(s) de 5;2;1;0.
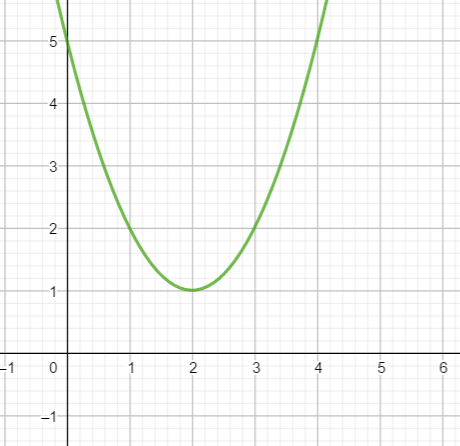
Pour trouver les antécédents éventuels de 5
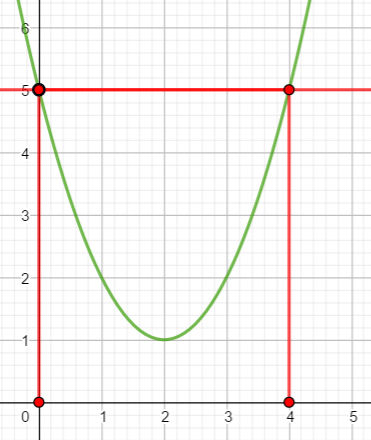
Je place 5 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 5 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 5.
Les antécédents de 5 sont 0 et 4.
Je valide ma réponse en vérifiant que les points de coordonnées (0;5) et (4;5) sont sur la courbe.
Pour trouver les antécédents éventuels de 2
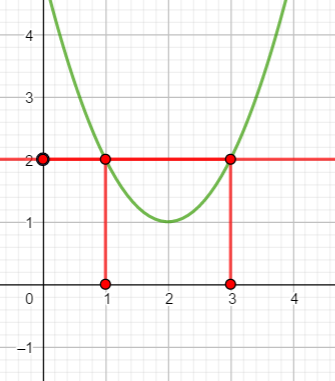
Je place 2 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 2 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 2.
Les antécédents de 2 sont 1 et 3.
Je valide ma réponse en vérifiant que les points de coordonnées (1;2) et (3,2) sont sur la courbe.
Pour trouver les antécédents éventuels de 1
Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Ici je repère le point d’intersection avec la courbe. L’abscisse de ce point est l’ antécédent de 1.
L’antécédent de 1 est 2.
Je valide ma réponse en vérifiant que le point de coordonnées (2;1) est sur la courbe.
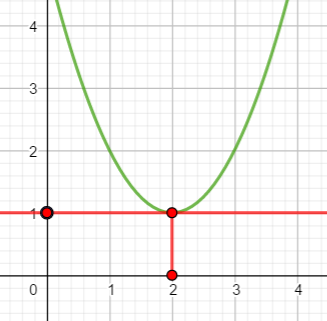
Pour trouver les antécédents éventuels de 0
Je place 0 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 0 toute entière (c’est l’axe des abscisses). Ici il n’y a pas de point d’intersection avec la courbe.
0 n’a pas d’antécédent.