Sommaire
La suite est définie par récurrence
Recommandation
On calcule le terme suivant en fonction du précédent donc pour calculer, par exemple, u_7 il faut connaître u_6 et pour connaître u_6 il faut connaître u_5, ….
On voit que cette formule convient pour calculer les premiers termes d’une suite mais pas des termes éloignés.
Méthode 1 (par le calcul) :
Lorsqu’on veut calculer, par exemple u_7, il faut remplacer tous les n par l’entier précédent, ici 6 dans la formule u_{n+1}=f(u_n) puis on calcule en respectant la priorité des opérations.
Méthode 2 ( avec la calculatrice TI 83 Premium CE Python):
Par exemple : générons la suite
u_{0}=10 et u_{n+1}=2*u_{n}+1

Méthode 3 ( avec un tableur):
Lorsque la suite (u_n) est définie par récurrence, une seule colonne est nécessaire pour générer la suite.
Par exemple : générons la suite
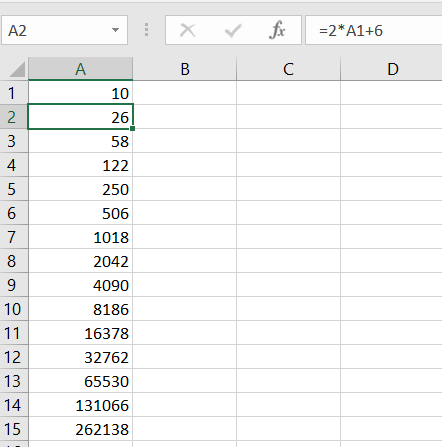
u_{0}=10 et u_{n+1}=2*u_{n}+6
Dans la cellule A1 : saisir la valeur u_0 c’est-à-dire 10
Dans la cellule A2 : saisir la formule =2*A1+6 puis recopier la formule vers le bas.
Voici une fenêtre active géogébra où on peut utiliser le tableur pour conjecturer ou vérifier les résultats obtenus pour le calcul des termes de la suite dans les exercices ci-dessous.
Exercice 1
Calculer u_1 ,u_2 et u_3 .(Comme on demande de calculer, il faut utiliser la méthode n°1. Cependant on peut conjecturer d’abord avec la calculatice et ensuite vérifier avec un tableur )
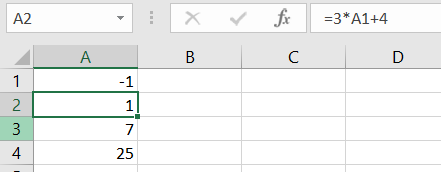
u_{n+1}=3u_{n}+4 et u_0=-1
Exercice 2
Calculer u_1 ,u_2 et u_3 .(Comme on demande de calculer, il faut utiliser la méthode n°1. Cependant on peut conjecturer d’abord avec la calculatice et ensuite vérifier avec un tableur )
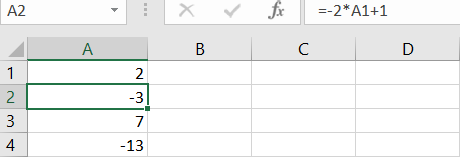
u_{n+1}=-2u_{n}+1 et u_0=2
Exercice 3
Calculer u_1 ,u_2 et u_3 .(Comme on demande de calculer, il faut utiliser la méthode n°1. Cependant on peut conjecturer d’abord avec la calculatice et ensuite vérifier avec un tableur )
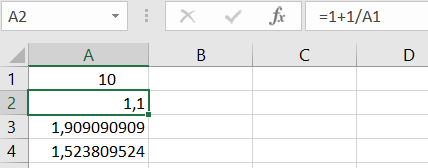
u_{n+1}=\frac{1}{u_{n}}+1 et u_0=10
La suite est définie par formule explicite
Méthode 1 (par le calcul) :
Lorsqu’on veut calculer, par exemple u_6, il faut remplacer tous les n par l’entier , ici 6 dans la formule u_{n}=f(n) puis on calcule en respectant la priorité des opérations.
Méthode 2 ( avec la calculatrice TI 83 Premium CE Python):

Méthode 3 (avec un tableur):
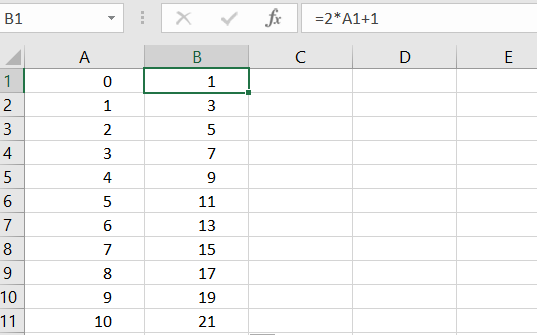
Lorsque la suite (u_n) est définie par formule explicite, deux colonnes sont nécessaires pour générer la suite : une pour les indices n et une autre pour les termes de la suite (u_n)
Par exemple : générons la suite
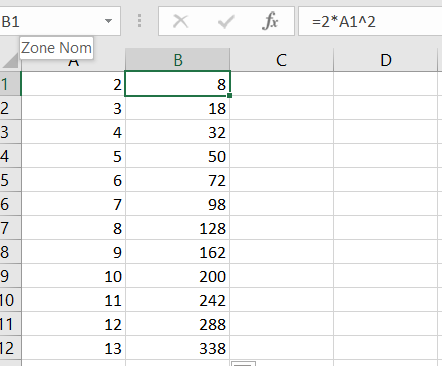
u_{n}=2n^2 pour n\geq 2
Attention : il y a un piège, la suite commence au rang ou indice 2.
Dans la cellule A1 : saisir la valeur du premier rang ou indice, ici 2.
Dans la cellule B1 : saisir la formule =2*A1^2 puis recopier la formule vers le bas.
Voici une fenêtre active géogébra où on peut utiliser le tableur pour conjecturer ou vérifier les résultats obtenus pour le calcul des termes de la suite dans les exercices ci-dessous.
Exercice 4
Calculer u_0 ,u_5 et u_{10} .(Comme on demande de calculer, il faut utiliser la méthode n°1. Cependant on peut conjecturer d’abord avec la calculatice et ensuite vérifier avec un tableur )
u_{n}=2n+1 pour n \in \mathbf{N}
Exercice 5
Calculer u_0 ,u_4 et u_{8} .(Comme on demande de calculer, il faut utiliser la méthode n°1. Cependant on peut conjecturer d’abord avec la calculatice et ensuite vérifier avec un tableur )
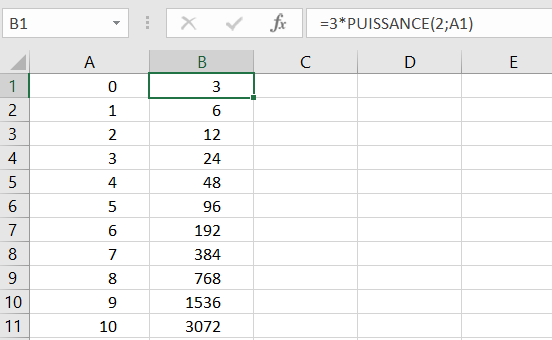
u_{n}=3\times 2^n pour n \in \mathbf{N}
Exercice 6
Calculer u_1 ,u_7 et u_{9} .(Comme on demande de calculer, il faut utiliser la méthode n°1. Cependant on peut conjecturer d’abord avec la calculatice et ensuite vérifier avec un tableur )
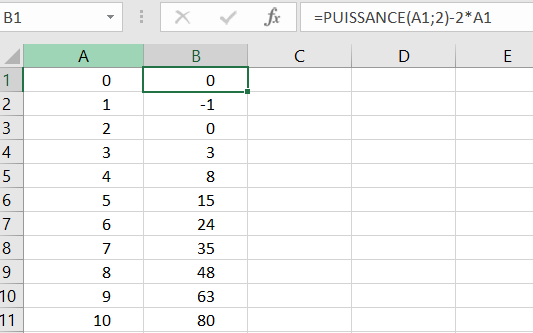
u_{n}=n^2-2n pour n \in \mathbf{N}