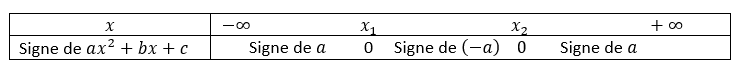Sommaire
Enoncé du problème
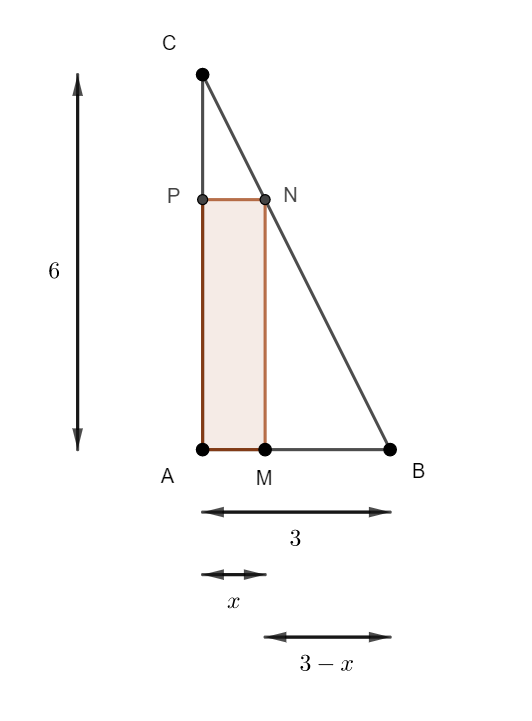
ABC est un triangle rectangle en A tel que AB = 3 et AC = 6.
M est un point variable sur le segment [AB]
On construit le rectangle AMNP tels que N et P se trouvent respectivement sur les segments [BC] et [AC] .
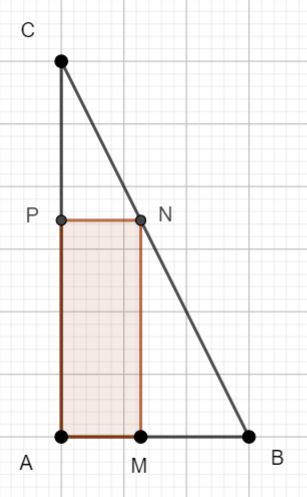
Où placer le point M pour que l’aire du rectangle AMNP soit la plus grande possible ?
Construction de la figure à l’aide du logiciel Géogébra
Construire la figure dans la fenêtre Géogébra ci-dessous :
Résolution géométrique à l’aide du logiciel Géogébra
Résolution graphique à l’aide d’une courbe obtenue avec le logiciel Géogébra en ajustant un nuage de points
Résolution algébrique
- On pose x la distance AM, le but du paragraphe 1 est d’exprimer l’aire de AMNP en fonction de x.
a. Appliquer le théorème de THALES dans le triangle ABC et en déduire la distance MN en fonction de x.
b. Montrer alors que l’aire de AMNP vaut -2x^{2}+6x
2) On note f(x)=-2x^{2}+6x pour x\in [0;3]
a) Calculer f'(x)
b) Etudier le signe de f'(x) pour x\in [0;3]
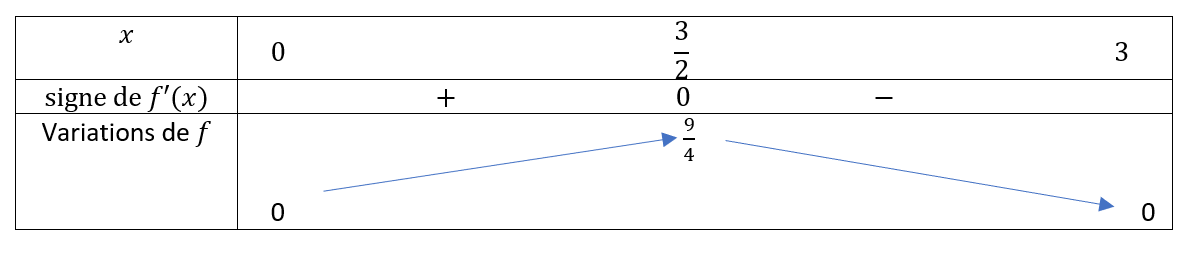
c) En déduire le tableau de variations de la fonction f sur l’intervalle [0;3]. Puis répondre à la question posée.