Sommaire
Préambule
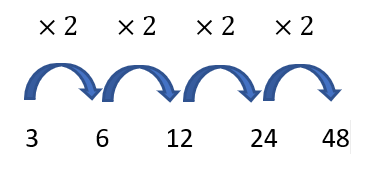
Voici cinq termes qui se déduisent les uns des autres en multipliant par 2. Pour trouver le suivant, c’est facile il suffit de faire 48\times2=96. Mais si on vous demande de déterminer le 100ème terme de cette suite, cela devient plus compliqué. Cette fiche de cours doit pouvoir nous permettre de répondre à cette question et bien d’autres.
Définition (générer une suite géométrique par récurrence)
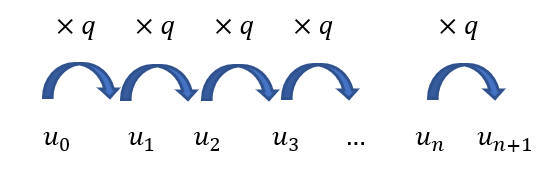
On dit qu’une suite (u_n) définie sur \mathbf{N} est géométrique quand il existe un réel q appelé raison de la suite tel que, pour tout entier naturel n , u_{n+1}=q\times {u_n} .
Propriété (générer une suite géométrique par formule explicite)
Activité d’approche
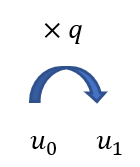
A l’aide du schéma ci-contre, expliquer comment on passe de u_0 à u_1 puis compléter les pointillés dans l’égalité suivante :
u_1=u_0\times q^{…}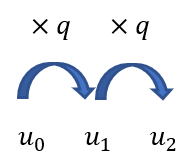
A l’aide du schéma ci-contre, expliquer comment on passe de u_0 à u_2 puis compléter les pointillés dans l’égalité suivante :
u_2=u_0\times q^{…}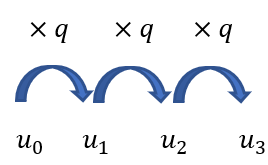
A l’aide du schéma ci-contre, expliquer comment on passe de u_0 à u_3 puis compléter les pointillés dans l’égalité suivante :
u_3=u_0\times q^{…}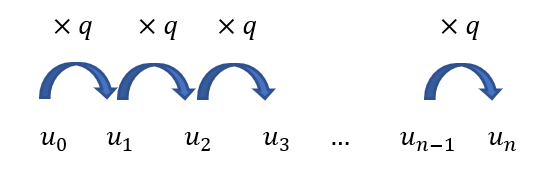
A l’aide du schéma ci-contre, expliquer comment on passe de u_0 à u_n puis compléter les pointillés dans l’égalité suivante :
u_n=u_0\times q^{…}Propriété 1
quand on exprime u_n en fonction de u_0
Une suite (u_n) définie sur \mathbf{N} est géométrique si et seulement si pour tout entier naturel n , u_n=u_0q^n .
Activité d’approche
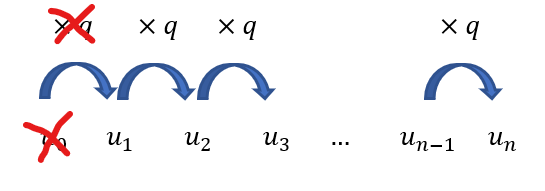
A l’aide du schéma ci-contre, expliquer comment on passe de u_1 à u_n puis compléter les pointillés dans l’égalité suivante :
u_n=u_1q^{…}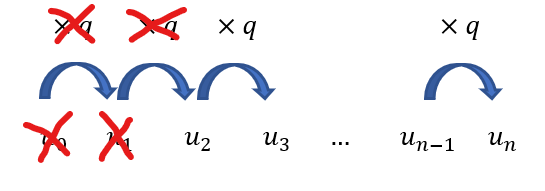
A l’aide du schéma ci-contre, expliquer comment on passe de u_2 à u_n puis compléter les pointillés dans l’égalité suivante :
u_n=u_2q^{…}Propriété 2
quand on exprime u_n en fonction de u_p
Une suite (u_n) définie sur \mathbf{N} est géométrique si et seulement si pour tout entier naturel n ,
u_n=u_pq^{n-p} .
Exercice n°1
Pour chacune des suites ci-dessous, indiquer en justifiant si elles sont géométriques et si oui indiquer la raison.
- u_0=2 et u_{n+1}=0.5u_n
2. u_0=1 et u_{n+1}=3u_{n}+1
3. u_0=0.8 et u_{n+1}=(u_{n})^2
Exercice n°2
Pour chacune des suites ci-dessous, indiquer en justifiant si elles sont géométriques et si oui indiquer la raison.
- u_{n}=2^n , pour n \in \mathbf{N}
2. u_{n}=3n, pour n \in \mathbf{N}
3. u_{n}=-2\times3^n
Variations d’une suite géométrique
Exemple n°1 : u_0 est positif et q>1
On considère la suite géométrique définie par
u_0=0.5 et u_{n+1}=3u_{n}.
On programme la calculatrice et sur le graphique, on fait apparaître les points de coordonnées (n;u_n).

Il semble que quand les abscisses n augmentent les ordonnées u_n augmentent. On dit que la suite est croissante.
Exemple n°2 : u_0 est positif et 0<q<1
On considère la suite géométrique définie par
u_n=2(\frac{1}{2})^n.
On programme la calculatrice et sur le graphique, on fait apparaître les points de coordonnées (n;u_n).
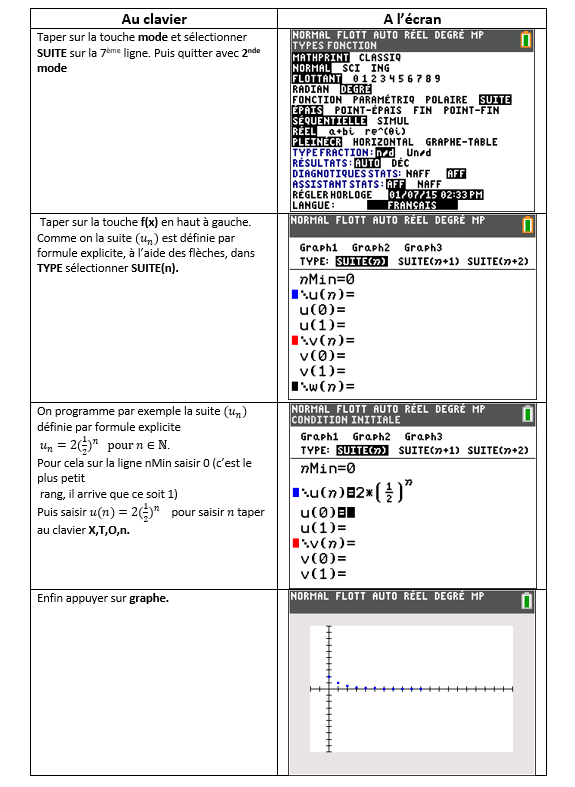
Il semble que quand les abscisses n augmentent les ordonnées u_n diminuent. On dit que la suite est décroissante.
Exemple n°3 : u_0 est négatif et 0<q<1
On considère la suite géométrique définie par
u_0=0.5 et u_{n+1}=3u_{n}.
On programme la calculatrice et sur le graphique, on fait apparaître les points de coordonnées (n;u_n).

Il semble que quand les abscisses n augmentent les ordonnées u_n augmentent. On dit que la suite est croissante.
Exemple n°4 : u_0 est négatif et q>1
On considère la suite géométrique définie par
u_n=-\frac{1}{8}\times {2^n}.
On programme la calculatrice et sur le graphique, on fait apparaître les points de coordonnées (n;u_n).

Il semble que quand les abscisses n augmentent les ordonnées u_n diminuent. On dit que la suite est décroissante.
Propriété 3
Exercice n°3
Pour chacune des suites géométriques ci-dessous, déterminer la raison q et le premier terme u_0. Puis à l’aide de la propriété n°3, en déduire les variations de la suite.
- u_0=-2 et u_{n+1}=3u_{n}
2. u_{n}=-2\times(\frac{1}{3})^n , n \in \mathbf{N}
3. u_0=5 et u_{n+1}=6u_{n}
4. u_{0}=14 et u_{n+1}=\frac{1}{2}u_n .
5. u_{0}=2 et u_{n+1}=-\frac{1}{2}u_n .









