Sommaire
Activité d’approche
dans cette activité, nous allons étudier dans quel ordre sont rangés les termes des suites suivantes.
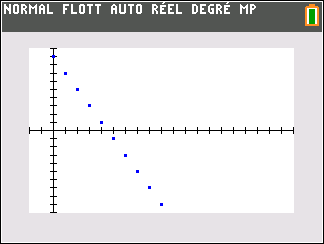
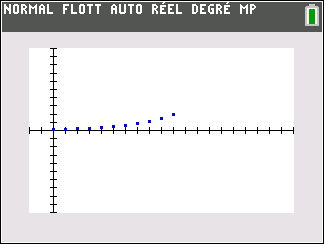
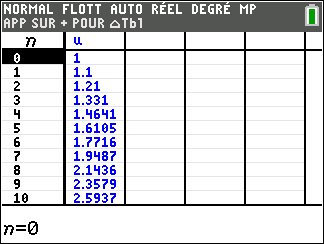
suite n°1 : u_n= -2+\frac{1}{2}n
Tout d’abord, on programme la suite sur la calculatrice TI 83 Premium et on examine tableur et représentation graphique ci-dessous :

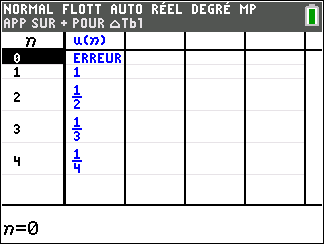
Dans la deuxième colonne , les nombres u_n semblent rangés dans l’ordre croissant, c’est-à-dire que le terme précédent est toujours plus petit que le terme suivant. Ce qui se note :
u_n<u_{n+1} pour n\in \mathbf{N}
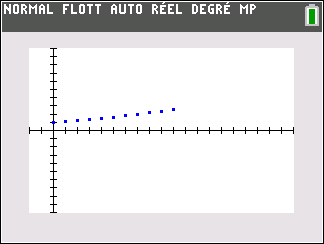
Les points dans le repère ont pour coordonnées(n;u_n). Il semble que quand les n augmentent , les u_n augmentent aussi.
Ce qui se note :
u_n<u_{n+1} pour n\in \mathbf{N}
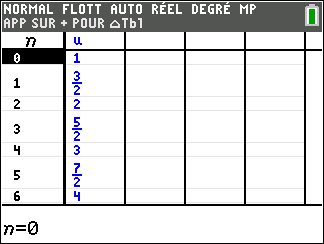
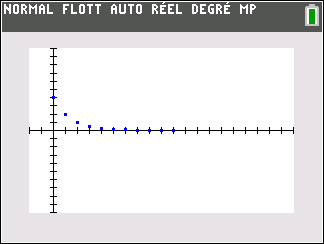
suite n°2 : u_n= \frac{1}{n+0.25}
Tout d’abord, on programme la suite sur la calculatrice TI 83 Premium et on examine tableur et représentation graphique ci-dessous :
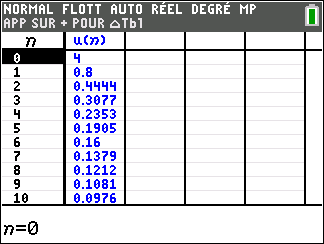
Dans la deuxième colonne , les nombres u_n semblent rangés dans l’ordre décroissant, c’est-à-dire que le terme précédent est toujours plus grand que le terme suivant. Ce qui se note :
u_n>u_{n+1} pour n\in \mathbf{N}
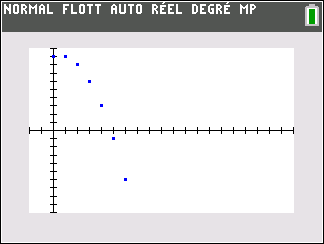
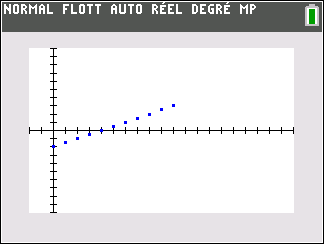
Les points dans le repère ont pour coordonnées(n;u_n). Il semble que quand les n augmentent , les u_n diminuent.
Ce qui se note :
u_n>u_{n+1} pour n\in \mathbf{N}
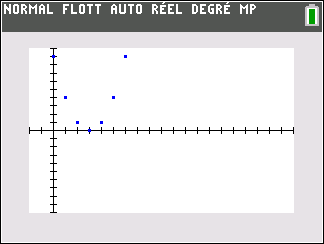
suite n°3 : u_n=(n-2)^2
Tout d’abord, on programme la suite sur la calculatrice TI 83 Premium et on examine tableur et représentation graphique ci-dessous :

Dans la deuxième colonne , les nombres u_n semblent rangés dans l’ordre décroissant puis dans l’ordre croissant à partir n=2 . Ce qui se note :
u_n<u_{n+1} pour n\geq 2.
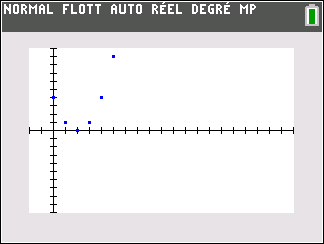
Les points dans le repère ont pour coordonnées(n;u_n). Il semble que quand les n augmentent , les u_n diminuent puis augmentent à partir de n=2.
Ce qui se note :
u_n<u_{n+1} pour n\geq2
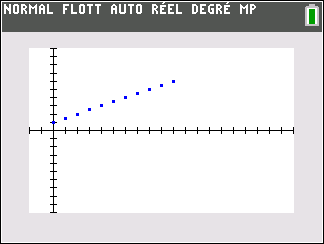
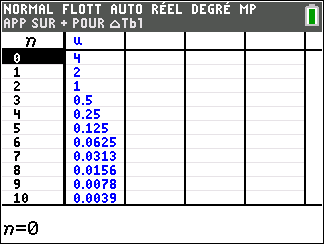
suite n°4 : u_0=0.25 et u_{n+1}=2u_n
Tout d’abord, on programme la suite sur la calculatrice TI 83 Premium et on examine tableur et représentation graphique ci-dessous :
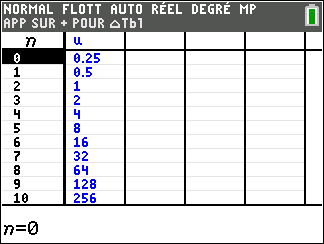
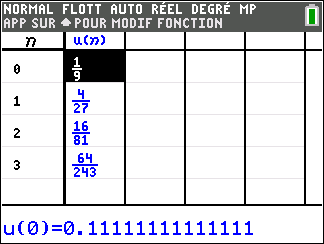
Dans la deuxième colonne, les nombres u_n semblent rangés dans l’ordre croissant. Ce qui se note :
u_n<u_{n+1} pour n\in \mathbf{N}.

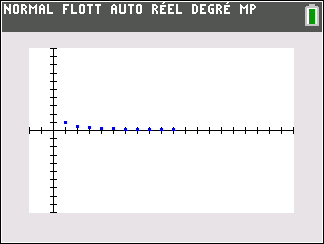
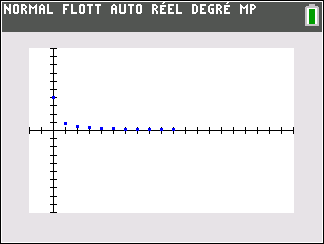
Les points dans le repère ont pour coordonnées(n;u_n). Il semble que quand les n augmentent , les u_n augmentent .
Ce qui se note :
u_n<u_{n+1} pour n\in \mathbf{N}.
Définitions
Une suite (u_n) est croissante à partir d’un rang p si pour tout n\geq p on a u_n\leq u_{n+1} ( le terme précédent est plus petit que le terme suivant )
Une suite (u_n) est décroissante à partir d’un rang p si pour tout n\geq p on a u_n\geq u_{n+1} ( le terme précédent est plus grand que le terme suivant )
Méthodes
Méthode n°1
Je calcule u_{n+1}-u_n et j’étudie son signe .
Si le signe est +, u_{n+1}-u_n\geq 0 et la suite (u_n) est croissante.
Si le signe est –, u_{n+1}-u_n\leq 0 et la suite (u_n) est décroissante.
Méthode n°2
Si les termes de la suite sont strictement positifs, je calcule \frac{u_{n+1}}{u_n} et je compare le résultat obtenu à 1 .
Si \frac{u_{n+1}}{u_n}\geq 1 la suite (u_n) est croissante.
Si \frac{u_{n+1}}{u_n}\leq 1 la suite (u_n) est décroissante.
Méthode n°3
Si la suite (u_n) est définie de façon explicite c’est-à-dire u_n=f(n)
J’étudie les variations de f sur [0;+\infty[. Ce seront les mêmes que celles de la suite (u_n).
Exemple n°1
Reprenons la suite n°4 de l’activité d’approche u_0=0.25 et u_{n+1}=2u_n. Nous avions conjecturé qu’elle était croissante, démontrons-le.
Compte-tenu de l’écriture par récurrence de la suite (u_n) , on va utiliser la méthode n°2.
Les termes de la suite sont positifs.
Je calcule
\frac{u_{n+1}}{u_n}=\frac{2u_n}{u_n}On simplifie la fraction par u_n
\frac{u_{n+1}}{u_n}=2Comme 2>1 , \frac{u_{n+1}}{u_n}>1 et donc la suite (u_n) est croissante.
Exemple n°2
Reprenons la suite n°1 de l’activité d’approche u_n= -2+\frac{1}{2}n. Nous avions conjecturé qu’elle était croissante, démontrons-le.
Compte-tenu de l’écriture par formule explicite de la suite (u_n) , on va utiliser la méthode n°3.
On va étudier les variations de la fonction affine f(x)= -2+\frac{1}{2}x sur ]0;+\infty[.
Comme le coefficient a=\frac{1}{2}, il est positif donc la fonction affine f est croissante sur ]0;+\infty[.
Et donc la suite (u_n) est croissante.
Exemple n°3
Reprenons la suite n°3 de l’activité d’approche u_n=(n-2)^2. Nous avions conjecturé qu’elle était croissante à partir du rang 2, démontrons-le.
Compte-tenu de l’écriture par formule explicite de la suite (u_n) , on va utiliser la méthode n°1.
On va d’abord calculer u_{n+1}-u_n en remplaçant u_{n+1} par ((n+1)-2)^2 et u_{n} par (n-2)^2
u_{n+1}-u_n=((n+1)-2)^2-(n-2)^2
\hspace{1.6cm}=((n-1)^2-(n-2)^2
\hspace{1.6cm}=(n^2-2n+1)-(n^2-4n+4)
\hspace{1.6cm}=n^2-2n+1-n^2+4n-4
\hspace{1.6cm}=2n-3
Pour étudier le signe de 2n-3, on peut , par exemple, utiliser un résultat de seconde connu pour étudier le signe de ax+b:
a=2 , b=-3 et -\frac{b}{a}=-\frac{-3}{2}=\frac{3}{2}
On fait le tableau de signes sur [0;+\infty[

En réalité, n est un entier naturel, donc 2n-3 est positif pour n\geq 2.
Et donc la suite (u_n) est croissante à partir du rang 2.
Voici une fenêtre active géogébra pour générer les termes des suites des exercices suivants et conjecturer ou vérifier vos résultats.