Sommaire
Définition d’une suite arithmético-géométrique
Une suite (u_n) est arithmético-géométrique lorsque (u_n) est définie par une formule de récurrence de la forme u_{n+1}=au_n+b avec a et b réels.
Exemple 1
On considère la suite (u_n) arithmético-géométrique définie par une formule de récurrence u_{n+1}=-0.2u_n+1 et u_0=2 .
Calculer u_1 , u_2 , u_3 et u_4
Exemple 2
On considère la suite (u_n) arithmético-géométrique définie par une formule de récurrence u_{n+1}=0.5u_n+2 et u_0=1 .
Calculer u_1 , u_2 , u_3 et u_4
Représentation graphique d’une suite arithmético-géométrique
On considère la suite arithmético-géométrique (u_n) définie par une formule de récurrence u_{n+1}=0.25u_n+3 avec u_0=1.
On a u_{n+1}=f(u_n) avec f(x)=0.25x+3.
On explique ci-dessous comment obtenir graphiquement les termes de la suite sur l’axe des abscisses.
- tracer la courbe de f(x)=0.25x+3 qui est une droite ( elle est en vert dans les repères ci-dessous.)
- tracer la droite d’équation y=x , elle est en noir dans les repères ci-dessous et ses points ont la particularité d’avoir l’abscisse égale à l’ordonnée.
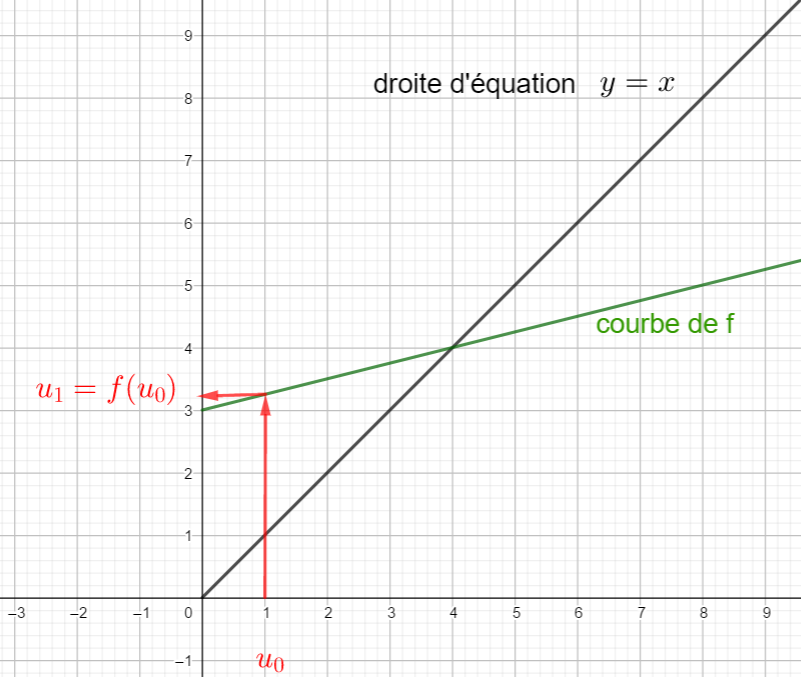
3. placer u_0 sur l’axe des abscisses et construire graphiquement à l’aide de la courbe de f ( elle est en vert dans le repère ) son image f(u_0) qui est u_1
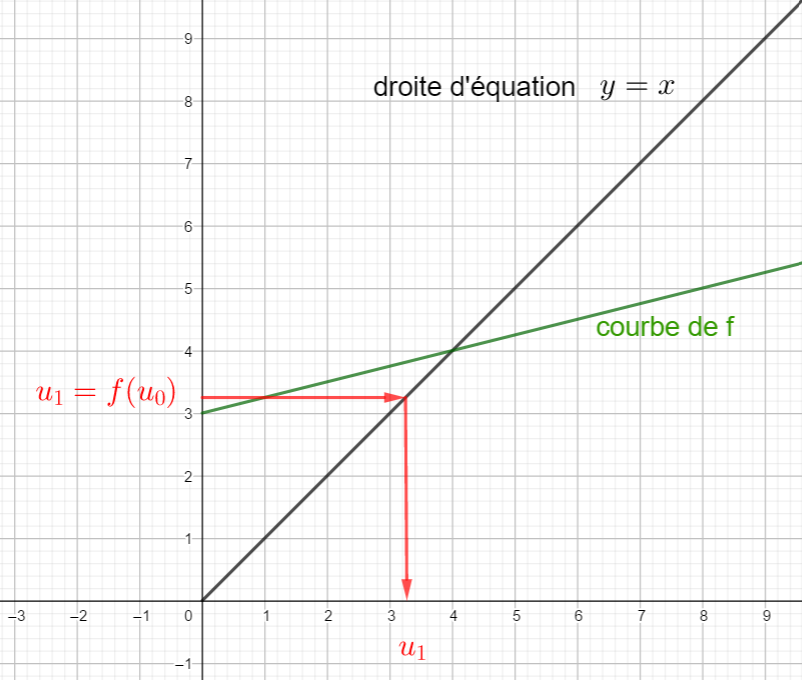
4. construire graphiquement l’antécédent de u_1 l’aide de la droite d’équation y=x ( elle est en noir dans le repère ) son antécédent est u_1 car les points de la droite d’équation y=x ont leur abscisse égale à leur ordonnée. Je place u_1 sur l’axe des abscisses.
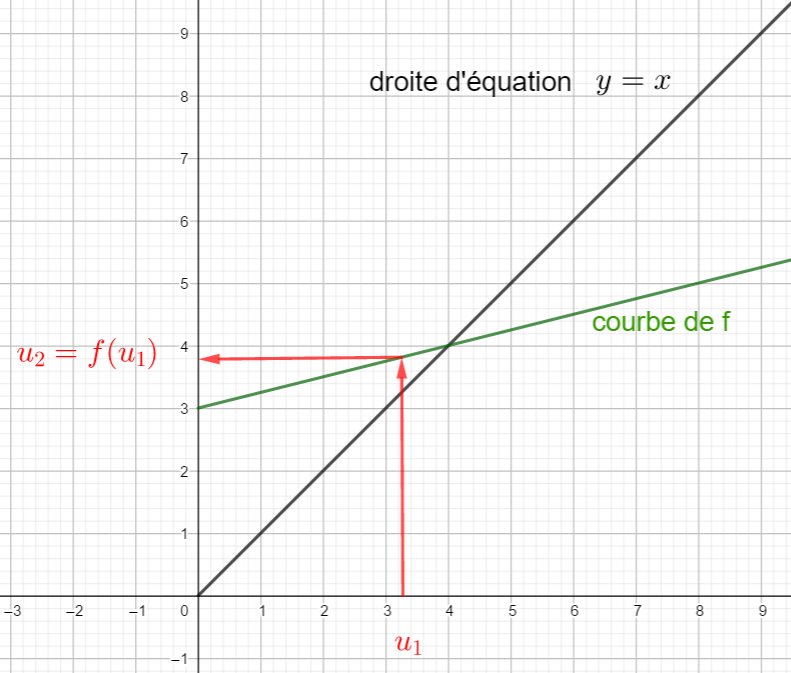
5. construire graphiquement à l’aide de la courbe de f ( elle est en vert dans le repère ) l’ image de u_1 , f(u_1) qui est u_2. Puis continuer le procédé autant de fois qu’il est nécessaire.
Limite d’une suite arithmético-géométrique
On considère la suite (u_n) arithmético-géométrique définie par une formule de récurrence u_{n+1}=0.5u_n+2 et u_0=1 .
Calculer u_1 , u_2 , u_3 et u_4
cas n°1 :
On considère la suite (u_n) arithmético-géométrique définie par une formule de récurrence u_{n+1}=0.2u_n+5 et u_0=1 .
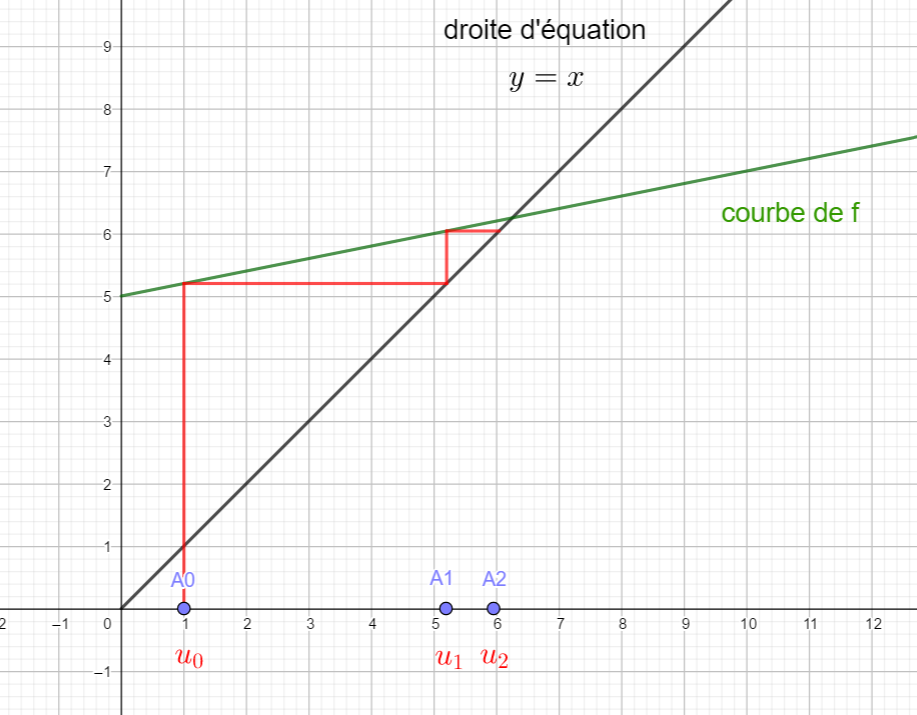
Graphiquement, on constate que la suite tend vers l’abscisse du point d’intersection des deux droites qu’on a coutume de noter l.
lim_{n\to{+\infty}}u_n=lcas n°2 :
On considère la suite (u_n) arithmético-géométrique définie par une formule de récurrence u_{n+1}=2u_n+1 et u_0=1 .
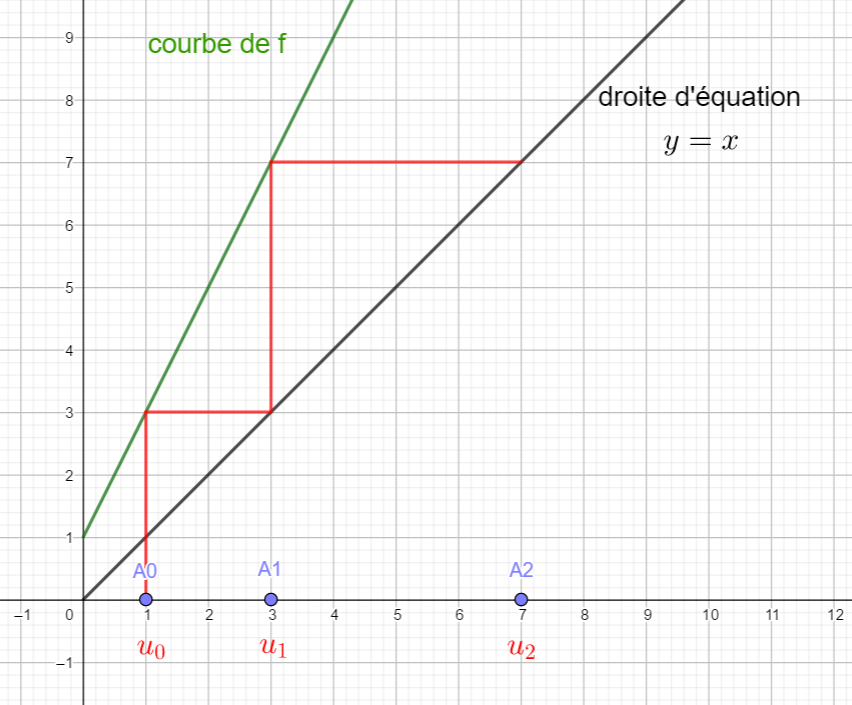
Graphiquement, on constate que la suite tend vers +\infty.
lim_{n\to{+\infty}}u_n=+\inftyOn reprend l’exemple n°1 mais on le traite graphiquement
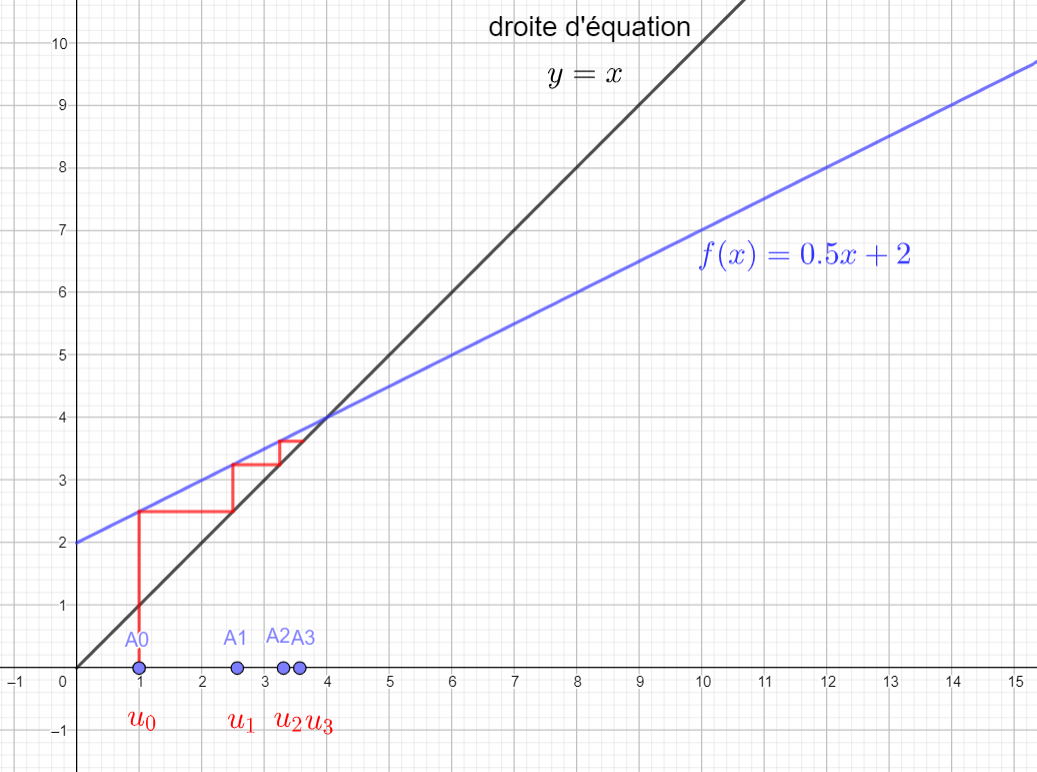
On considère la suite (u_n) arithmético-géométrique définie par une formule de récurrence u_{n+1}=0.5u_n+2 et u_0=1 .
Construire u_1 , u_2 et u_3 sur l’axe des abscisses. Conjecturer ensuite la limite de la suite (u_n).