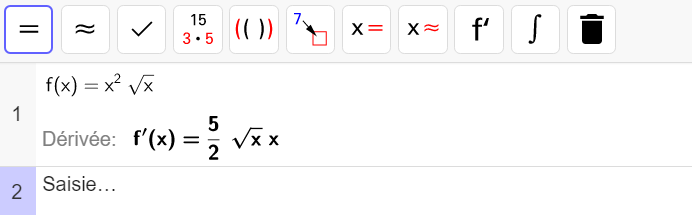
f(x)= x^2\sqrt{x} pour x\in ]0;+\infty[
1.On veut calculer f'(x).
On répond à la question suivante : f(x) est-elle une somme, le produit d’un réel par une fonction, le produit de deux fonctions, l’inverse d’une fonction ou le quotient de deux fonctions ?
C’est le produit de deux fonctions u\times v avec u(x)=x^2 et v(x)=\sqrt{x}.
On va utiliser la ligne n°3 du tableau n°1 ci-dessous.
f(x) est | f'(x) se calcule ainsi : |
une somme u+v | u’+v’ |
le produit d’une constante k par une fonction u c’est-à-dire ku | k\times u’ |
un produit de deux fonctions u\times v | u’\times v+u\times v’ |
l’inverse d’une fonction \frac{1}{u} | -\frac{u’}{u^2} |
un quotient \frac{u}{v} | \frac{u’\times v-u\times v’}{v^2} |
2a.on veut calculer la dérivée u'(x)
u(x)=x^2 est une fonction de référence, on utilise la ligne carré du tableau n°2 ci-dessous
u'(x)=2x
2b.on veut calculer la dérivée v'(x)
v(x)=\sqrt{x}est une fonction de référence, on utilise la ligne racine carrée du tableau n°2 ci-dessous
v'(x)=\frac{1}{2\sqrt{x}}
Fonction | f(x) | Dérivable sur… | f'(x) |
constante | f(x)=k | \mathbf{R} | f'(x)=0 |
identité | f(x)=x | \mathbf{R} | f'(x)=1 |
carré | f(x)=x^2 | \mathbf{R} | f'(x)=2x |
cube | f(x)=x^3 | \mathbf{R} | f'(x)=3x^2 |
inverse | f(x)=\frac{1}{x} | \left]-\infty;0\right[\cup\left]0;+\infty\right[ | f'(x)=-\frac{1}{x^2} |
racine carrée | f(x)=\sqrt{x} | ]0;+\infty[ | f'(x)=\frac{1}{2\sqrt{x}} |
3. On calcule la dérivée f'(x)
On remplace u par x^2, v par \sqrt{x}, u’ par 2x et v’ par \frac{1}{2\sqrt{x}} dans la formule u’\times v+u\times v’
f'(x)=2x\times{\sqrt{x}}+{x^2}\times{\frac{1}{2\sqrt{x}}}
Voilà ce qu’il faut écrire sur votre copie :
f'(x)= (x^2\sqrt{x})’\\f'(x)=(x^2)’\times{\sqrt{x}}+x^2\times{\sqrt{x}’} \\f'(x)=2x\sqrt{x}+{x^2}\times{\frac{1}{2\sqrt{x}}}On peut s’arrêter là…Pour les plus curieux, poursuivez !
On peut simplifier le deuxième terme de la somme par \sqrt{x}
f'(x)=2x\sqrt{x}+{x}\times{x}\times{\frac{1}{2\sqrt{x}}} \\f'(x)=2x\sqrt{x}+{x}\times{\sqrt{x}^2}\times{\frac{1}{2\sqrt{x}}} \\f'(x)=2x\sqrt{x}+{x}\times{\sqrt{x}}\times{\frac{1}{2}} \\f'(x)=2x\sqrt{x}+\frac{x\sqrt{x}}{2}On peut mettre au même dénominateur, ici 2
f'(x)={2x\sqrt{x}}\times{\frac{2}{2}}+\frac{x\sqrt{x}}{2} \\f'(x)=\frac{{2x\sqrt{x}}\times 2}{2}+\frac{x\sqrt{x}}{2} \\f'(x)=\frac{4x\sqrt{x}}{2}+\frac{x\sqrt{x}}{2} \\f'(x)=\frac{5x\sqrt{x}}{2}Valider avec Géogébra.