Soit la suite (u_n) définie par formule explicite par
u_n=n^2+2n+1.
Calculer u_0 , u_1 et u_{10}.
Méthode 1 ( par le calcul )
Pour calculer u_0, il faut remplacer tous les n par l’entier 0 dans la formule u_{n}=n^2+2n+1 puis on calcule en respectant la priorité des opérations.
u_{0}=0^2+2\times 0+1\\u_{0}=1Pour calculer u_1, il faut remplacer tous les n par l’entier 1 dans la formule u_{n}=n^2+2n+1 puis on calcule en respectant la priorité des opérations.
u_{1}=1^2+2\times 1+1\\u_{1}=1+2+1\\u_{1}=4Pour calculer u_{10}, il faut remplacer tous les n par l’entier 10 dans la formule u_{n}=n^2+2n+1 puis on calcule en respectant la priorité des opérations.
u_{10}=10^2+2\times 10+1\\u_{10}=100+20+1\\u_{10}=121Méthode 2 ( avec la calculatrice TI 83 Premium CE Python)

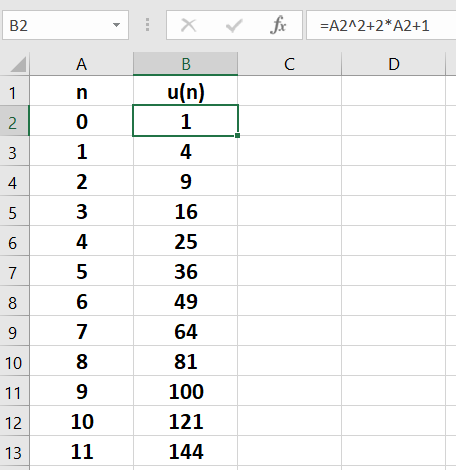
Méthode n°3 : Avec un tableur.
Comme la suite est définie par formule explicite, il faut deux colonnes : une pour les rangs : n et une pour les termes de la suite : u_n.
La formule à saisir dans la cellule B2 est en haut à droite de l’image.