Si les termes de la suite sont strictement positifs, je calcule \frac{u_{n+1}}{u_n} et je compare le résultat obtenu à 1 .
Si \frac{u_{n+1}}{u_n}\geq 1 la suite (u_n) est croissante.
Si \frac{u_{n+1}}{u_n}\leq 1 la suite (u_n) est décroissante.
Exemple
Etudier les variations de la suite (u_n) définie par formule explicite par u_n=\frac{n}{2n+1} pour n\in \mathbf{N}.
1.Conjecture à l’aide de la calculatrice.
Avant de se lancer dans les calculs, il paraît judicieux de programmer sa calculatrice et d’observer.
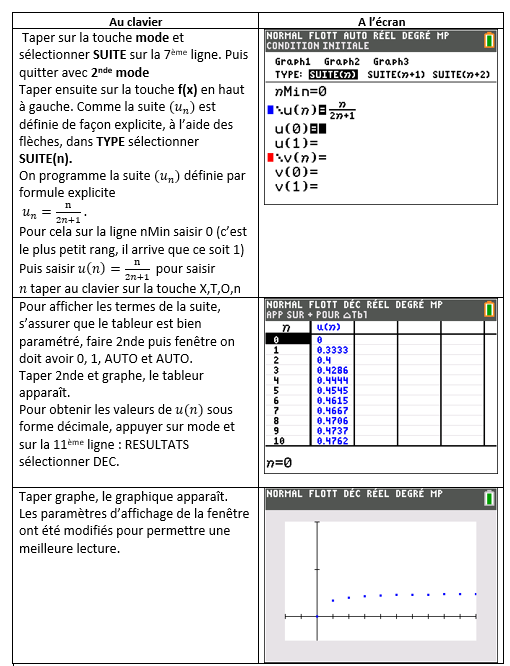
A l’aide de la calculatrice, on constate que les termes de la suite sont rangés dans l’ordre croissant.
2. On va utiliser la méthode ci-dessus pour étudier les variations de la suite (u_n).
Les termes de la suite sont positifs.
Etape n°1 : Je calcule \frac{u_{n+1}}{u_n}
Attention pour calculer u_{n+1}, je dois remplacer tous les n par (n+1) entre parenthèses dans l’expression u_n=\frac{n}{2n+1}.
\frac{u_{n+1}}{u_n}=\frac{\frac{(n+1)}{2(n+1)+1}}{\frac{n}{2n+1}}Diviser par \frac{n}{2n+1} revient à multiplier par son inverse \frac{2n+1}{n}.
\hspace{0.7cm}={\frac{n+1}{2(n+1)+1}}\times {\frac{2n+1}{n}}\\\hspace{0.7cm}={\frac{n+1}{2n+2+1}}\times {\frac{2n+1}{n}}\\\hspace{0.7cm}={\frac{n+1}{2n+3}}\times {\frac{2n+1}{n}}On applique la règle pour multiplier deux fractions.
\hspace{0.7cm}={\frac{(n+1)\times (2n+1)}{(2n+3)\times n}}\\\hspace{0.7cm}=\frac{2n^2+n+2n+1}{2n^2+3n}\\\hspace{0.7cm}=\frac{2n^2+3n+1}{2n^2+3n}Etape n°2 : je vais comparer \frac{u_{n+1}}{u_n} à 1.
1>0On ajoute de chaque côté 2n^2+3n, le sens de l’inégalité ne change pas.
2n^2+3n+1>2n^2+3nOn divise de chaque côté par le nombre strictement positif 2n^2+3n, le sens de l’inégalité ne change pas. \frac{2n^2+3n+1}{2n^2+3n}>1
Donc \frac{u_{n+1}}{u_n}>1
Donc la suite (u_n) est croissante.



