Si la suite (u_n) est définie de façon explicite c’est-à-dire u_n=f(n)
J’étudie les variations de f sur [0;+\infty[. Ce seront les mêmes que celles de la suite (u_n).
Exemple
Etudier les variations de la suite définie de façon explicite par u_n=n^3-3n.
1.Conjecture à l’aide de la calculatrice TI-83 Premium CE

On constate dans le tableur et sur le graphique que les termes de la suite (u_n) sont rangés dans l’ordre croissant à partir du rang 1.
2. Etude des variations de la suite (u_n) à l’aide de la méthode n°3.
Nous allons étudier les variations de la fonction f définie sur [0;+\infty[ par f(x)=x^3-3x.
Etape n°1 : calcul de f'(x).
On veut calculer f'(x).
On répond à la question suivante : f(x) est-elle une somme, le produit d’un réel par une fonction, le produit de deux fonctions, l’inverse d’une fonction ou le quotient de deux fonctions ?
C’est la somme de deux termes :
x^3 et -3x
La dérivée d’une somme est la somme des dérivées d’après le tableau n°1 ci-dessous
f(x) est | f'(x) se calcule ainsi : |
une somme u+v | u’+v’ |
le produit d’une constante k par une fonction u c’est-à-dire ku | k\times u’ |
un produit de deux fonctions u\times v | u’\times v+u\times v’ |
l’inverse d’une fonction \frac{1}{u} | -\frac{u’}{u^2} |
un quotient \frac{u}{v} | \frac{u’\times v-u\times v’}{v^2} |
Il faut donc calculer les dérivées des deux termes x^3 et -3x en utilisant le tableau n°2 ci-dessous et le tableau n°1 le cas échéant.
Fonction | f(x) | Dérivable sur… | f'(x) |
constante | f(x)=k | \mathbf{R} | f'(x)=0 |
identité | f(x)=x | \mathbf{R} | f'(x)=1 |
carré | f(x)=x^2 | \mathbf{R} | f'(x)=2x |
cube | f(x)=x^3 | \mathbf{R} | f'(x)=3x^2 |
inverse | f(x)=\frac{1}{x} | \left]-\infty;0\right[\cup\left]0;+\infty\right[ | f'(x)=-\frac{1}{x^2} |
racine carrée | f(x)=\sqrt{x} | ]0;+\infty[ | f'(x)=\frac{1}{2\sqrt{x}} |
| exponentielle | f(x)=e^x | \mathbf{R} | f'(x)=e^x |
(x^3)’=3x^2 d’après la ligne cube du tableau n°2
(-3x)’=-3(x)’ d’après la 2ème formule du tableau n°1 et (x)’=1 d’après la ligne identité du tableau n°2.
Donc (-3x)’=-3\times 1=-3
Voilà ce qu’il faut écrire sur votre copie :
f'(x)= (x^3-3x)’\\f'(x)= (x^3)’-(3x)’\\f'(x)=3x^2-3(x)’\\f'(x)=3x^2-3\times 1\\f'(x)= 3x^2-3Etape n°2 : étude du signe de la dérivée f'(x)= 3x^2-3.
C’est un polynôme du second degré, on utilise la 3me ligne du tableau ci-dessous.
- de nombres positifs alors la quantité est positive.
- de nombres négatifs alors la quantité est négative.
- de nombres de signes contraires ou indéterminés alors on ne peut pas conclure
On peut factoriser et étudier le signe d’un produit
On peut résoudre la quantité >0
…
On utilise le tableau suivant :

On utilise le résultat du cours suivant :
si \Delta>0
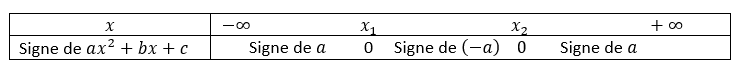
si \Delta=0

si \Delta<0

La quantité est toujours positive.
Exemples : les quantités x^2 , (2x+5)^4 sont toujours positives
La quantité est du signe de ce qui est élevé à la puissance.
Exemple : la quantité x^3 est du signe de x, la quantité (2x-1)^5 est du signe de 2x-1.
On étudie le signe des facteurs et on conclut avec la règle des signes. Si on ne peut pas conclure directement on fait un tableau de signes comme en seconde .
On étudie le signe du numérateur et le signe du dénominateur. On conclut avec la règle des signes. Si on ne peut pas conclure directement on fait un tableau de signes comme en seconde .
On calcule la dérivée, on étudie son signe et on fait le tableau de variations. Ensuite, sur la dernière ligne du tableau de variations, on lit le signe de la quantité.
J’identifie les coefficients a=3, b=0 et c=-3.
Je calcule \Delta=b²-4ac en remplaçant a,b,c par 3,0, (-3) .
\Delta=0²-4\times{3}\times{(-3)}\\\Delta=0+36\\\Delta=36Comme \Delta>0 , l’équation admet deux solutions réelles notées
x_1=\frac{-b-\sqrt{\Delta}}{2a} et x_2=\frac{-b+\sqrt{\Delta}}{2a}.
ax²+bx+c est du signe de a à l’extérieur des racines et du signe de (-a) à l’intérieur des racines.
Je calcule x_1=\frac{-b-\sqrt{\Delta}}{2a} en remplaçant a,b,\Delta par 3, 0, 36.
x_1=\frac{0-\sqrt{36}}{2\times{3}}\\x_1=\frac{(-6)}{6}\\x_1=-1Je calcule x_2=\frac{-b+\sqrt{\Delta}}{2a} en remplaçant a,b,\Delta par 3, 0, 36.
x_2=\frac{-0+\sqrt{36}}{2\times{3}}\\x_2=\frac{6}{6}\\x_2=1Je dresse le tableau de signes du polynôme sur l’intervalle [0;+\infty[
Comme a=1 le signe de a est positif.
Etape n°3 : variations de la suite (u_n)
Comme f'(x) est positif sur l’intervalle [1;+\infty[, la fonction f est croissante sur l’intervalle [1;+\infty[.
La suite (u_n) est donc croissante à partir du rang 1.



