Définition
Soit une suite (u_n) définie sur \mathbf{N}.
Si pour tout n de \mathbf{N}, u_{n+1}\geq u_n alors la suite est croissante sur \mathbf{N}.
Si pour tout n de \mathbf{N}, u_{n+1}\leq u_n alors la suite est décroissante sur \mathbf{N}.
Exemple n°1
Etudier les variations de la suite (u_n) définie par
u_n=2-3\times 0.6^n1.Conjecture à l’aide de la calculatrice TI-83 Premium CE

A l’aide de la calculatrice, on constate que les termes de la suite (u_n) sont rangés dans l’ordre croissant.
2. Etude des variations de la suite (u_n) en utilisant la définition.
Comme on a conjecturé le résultat à l’aide de la calculatice, on sait qu’on va obtenir u_{n+1}\geq u_n.
Nous allons écrire une démonstration du bas vers le haut en partant de la conclusion u_{n+1}\geq u_n, ce qui est interdit sauf si on écrit du bas vers le haut.
\hspace {1.6cm} 0.6\leq 1
\hspace {0.55cm} 0.6^n\times 0.6\leq 0.6^n
\hspace {1.15cm}0.6^{n+1}\leq 0.6^n
\hspace {0.3cm}-3\times 0.6^{n+1}\geq -3\times 0.6^n
\hspace {0cm}2-3\times 0.6^{n+1}\geq 2-3\times 0.6^n
\hspace {1.4cm}u_{n+1}\geq u_n
6.On divise par 0.6^n , le sens de l’inégalité ne change pas
5.On transforme 0.6^{n+1} en 0.6^n\times 0.6
4. On divise par -3 et le sens de l’inégalité change
3.On enlève 2 de chaque côté.
2.On remplace u_{n+1} et u_n par 2-3\times 0.6^{n+1} et 2-3\times 0.6^n.
1.On écrit la conclusion u_{n+1}\geq u_n sur la dernière ligne
Sur la copie, personne ne peut soupconner que cette démonstration a été écrite à l’envers.
On a donc montré que pour tout n de \mathbf{N}, u_{n+1}\geq u_n donc la suite est croissante sur \mathbf{N}.
Exemple n°2
Etudier les variations de la suite (u_n) définie par
u_n=2+\frac{5}{n+2}1.Conjecture à l’aide de la calculatrice TI-83 Premium CE
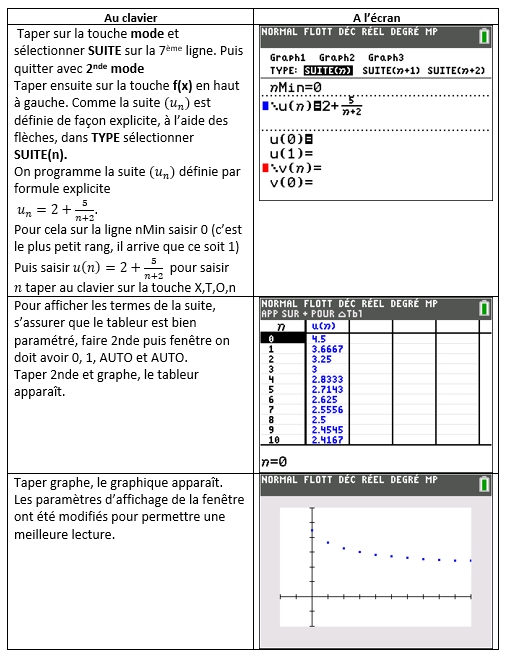
A l’aide de la calculatrice, on constate que les termes de la suite (u_n) sont rangés dans l’ordre décroissant.
2. Etude des variations de la suite (u_n) en utilisant la définition.
Comme on a conjecturé le résultat à l’aide de la calculatice, on sait qu’on va obtenir u_{n+1}\leq u_n.
Nous allons écrire une démonstration du bas vers le haut en partant de la conclusion u_{n+1}\leq u_n, ce qui est interdit sauf si on écrit du bas vers le haut.
\hspace {1.9cm} 3\geq 2
\hspace {1.3cm}n+3\geq n+2
\hspace {1.6cm}\frac{1}{n+3}\leq \frac{1}{n+2}
\hspace {1.6cm}\frac{5}{n+3}\leq \frac{5}{n+2}
\hspace {0.5cm}2+\frac{5}{(n+1)+2}\leq 2+\frac{5}{n+2}
\hspace {1.5cm}u_{n+1}\leq u_n
6. On enlève n , le sens de l’inégalité ne change pas
5. On utilise que la fonction inverse est décroissante : les nombres et les images varient en sens contraire.
4. On divise par 5 et le sens de l’inégalité ne change pas
3. On enlève 2 de chaque côté.
2. On remplace u_{n+1} et u_n par 2+\frac{5}{(n+1)+2} et 2+\frac{5}{n+2}.
1.On écrit la conclusion u_{n+1}\leq u_n sur la dernière ligne
Sur la copie, personne ne peut soupconner que cette démonstration a été écrite à l’envers.
On a donc montré que pour tout n de \mathbf{N}, u_{n+1}\leq u_n donc la suite est décroissante sur \mathbf{N}.



