Voici une vidéo où on résout l’inéquation (2x+1)^2<9, vous pouvez vous en inspirer pour résoudre (x-4)^2\leq 25.
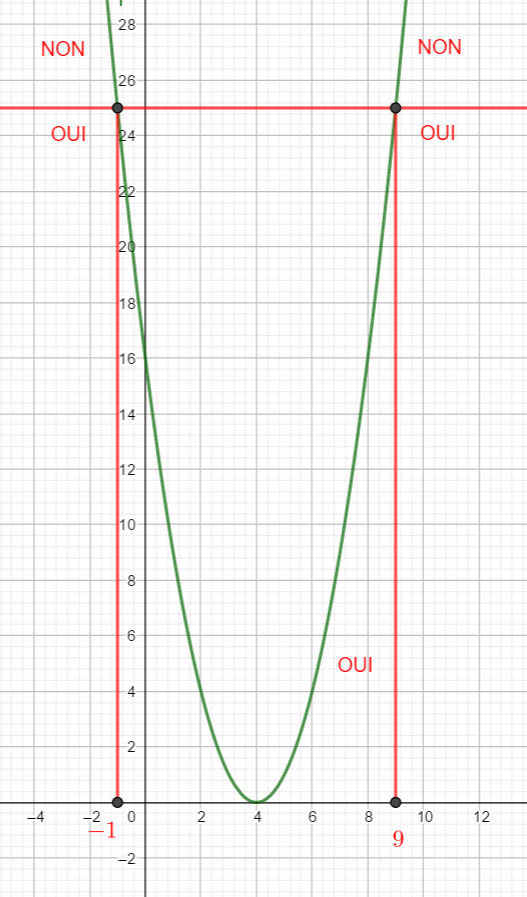
Résoudre dans \mathbf{R} l’ inéquation du second degré suivante : (x-4)^2\leq 25
Valider vos réponses avec la page géogébra ci-dessous. Pour cela saisir l’inéquation sur la ligne n°1 puis cliquer sur le 7ème onglet X=, à l’écran s’affiche l’intervalle solution sous forme d’inégalités.