logo

1. Fonction exponentielle

Sommaire

Définition et propriétés algébriques

Fonction exponentielle

Propriété et définition 

Il existe une fonction f et une seule définie et dérivable sur \mathbf{R} telle que :

pour tout x \in \mathbf{R} , f'(x)=f(x) et f(0)=1.

Cette fonction est appelée fonction exponentielle et notée exp : x \to exp(x)

Exercice n°1

Calculer f'(x) dans chaque cas.

Attention d’après la définition exp'(x)=exp(x).

  1. f(x)=exp(x)-x^2+1 sur \mathbf{R}.
correction

2. f(x)=x^2\times exp(x) sur \mathbf{R}.

correction

3. f(x)=\frac{exp(x)+1}{x^2+1} sur \mathbf{R}.

correction

Propriétés algébriques

Propriété

 Pour tous réels x et y, on a exp(x+y)=exp(x) \times exp(y).

Conséquence exp(nx)=exp(x) ^n

Exercice n°2

Utiliser la propriété ci-dessus pour simplifier les expressions suivantes dans chaque cas. 

  1. exp(3x-1)\times exp(2-2x).
correction

2. (exp(2x+1))^2. 

correction

3. exp(2-6x)\times exp(12+6x)

correction

4. exp(-x)(exp(x)+1)

correction

5. exp(x+1)\times exp(x-1).

correction

6. exp(1+3x)\times exp(2-3x).

correction

Propriété 

Pour tous réels x et y, on a  :  exp(-x)=\frac{1}{exp(x)}  et  exp(x-y)=\frac{exp(x)}{exp(y)} 

Démonstration 

1.exp(-x)=\frac{1}{exp(x)}

correction

2.exp(x-y)=\frac{exp(x)}{exp(y)}

correction

Exercice n°3

Utiliser les propriétés précédentes pour simplifier les expressions suivantes dans chaque cas. 

  1. \frac{exp(2x-1)}{exp(x+1)} 
correction

2. \frac{exp(3x)}{exp(2x+1)} 

correction

3.\frac{exp(x)}{exp(5x+5)} 

correction

4. \frac{exp(5x+3)\times exp(2x-1)}{exp(2x+1)}

correction

5. \frac{exp(1+x)\times exp(1-x)}{exp(2)}

correction

6. \frac{exp(2x-1)\times exp(2x+1)}{exp(2x)}

correction

Une nouvelle notation pour la fonction exponentielle 

On note  exp(1)=e, ce nombre est appelé nombre d’Euler, e \approx 2.718.

Théorème

Pour tout réel x ,   exp(x)=e^x.

Avec cette nouvelle notation, les propriétés précédentes s’écrivent

e^0=1, e^{x+y}=e^x\times e^y, e^{nx}=n e^x, e^{-x}=\frac{1}{e^x}, e^{x-y}=\frac{e^x}{e^y}.

Etude de la fonction exponentielle

Propriété

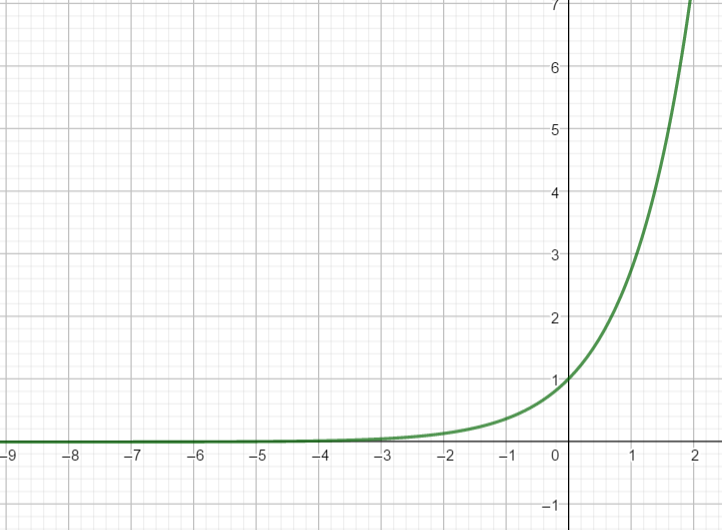
Pour tout réel x , e^x>0.

La fonction exponentielle est strictement positive.

Interprétation graphique : la courbe de la fonction exponentielle est toujours au-dessus de l’axe des abscisses.

Propriété

La fonction exponentielle est dérivable sur \mathbf{R} et  (e^x)’=e^x.

La fonction exponentielle est strictement croissante sur \mathbf{R}.

Propriété

Pour tous réels  a et  b, on a :

e^{a}=e^b \iff a=b.

e^{a}\leq e^b \iff a\leq b.

Pour les exercices 4, 5, 6 et 7 utiliser la page calcul formel de Géogébra ci-dessous pour conjecturer ou valider les réponses.

Exercice n°4

Résoudre les équations suivantes. 

  1. e^{x+1}=e^{2x+3} 
correction

2. e^{x^2}=e^{2x-1}

correction

3. \frac{e^{5x+1}}{e^{-4x+10}}=1 

correction

4. e^{2x-1}=e 

correction

5. e^{x^2+x+1}=1 

correction

6. e^{2x+2}\times e^{4x+10}=e 

correction

Exercice n°5

Résoudre les inéquations suivantes. 

  1. e^{5x-3}>e^{2x+3} 
correction

2. e^{x^2}\leq e^{3x-2}

correction

3. \frac{e^{2x+2}}{e^{-3x-13}}\geq 1 

correction

4. e^{6x-5}>e 

correction

5. e^{x^2+4x+4}>1 

correction

6. e^{x-2}\times e^{3x+1}\leq e 

correction

Exercice n°6

Calculer  f'(x) dans chaque cas. 

  1. f(x)=e^{x}-5 définie sur \mathbf{R}
correction

2.f(x)=3e^{x}+x^2 définie sur \mathbf{R}

correction

3.f(x)=xe^{x} définie sur \mathbf{R}

correction

4.f(x)=e^{x}(2x+5) définie sur \mathbf{R}

correction

5.f(x)=\frac{1}{e^{x}+10} définie sur \mathbf{R}

correction

6.f(x)=\frac{e^{x}-5}{2e^x+3} définie sur \mathbf{R}

correction

Propriété

Soient deux réels  a et  b.

La fonction g : x\to e^{ax+b} est dérivable sur \mathbf{R} et g'(x)=a\times e^{ax+b}

Exercice n°7

Calculer  f'(x) dans chaque cas. 

  1. f(x)=e^{2x-4}+1 définie sur \mathbf{R}
correction

2.f(x)=xe^{0.1x+0.2} définie sur \mathbf{R}

correction

3.f(x)=\frac{e^{2x}}{e^{2x}+1} définie sur \mathbf{R}

correction

Prolongement

Les fonctions  t\to e^{-kt} et t\to e^{kt} avec k>0.

  f_k : t\to e^{-kt} est définie et dérivable sur \mathbf{R}\\ f’_k(t)=-ke^{-kt}, donc f’_k(t)<0 et donc f_k est strictement décroissante sur f_k

g_k : t\to e^{kt} est définie et dérivable sur \mathbf{R}\\ g’_k(t)=ke^{kt}, donc g’_k(t)>0 et donc g_k est strictement croissante sur \mathbf{R}.

Exercice n°8

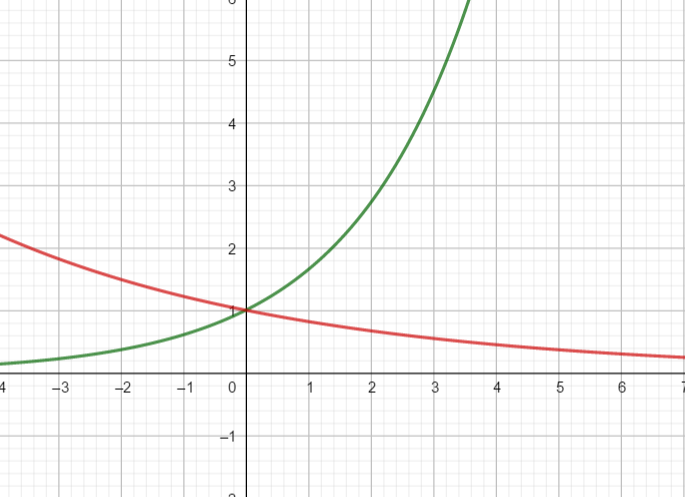
Dans le repère ci-dessous, on a représenté les fonctions suivantes :

f(t)=e^{0.5t} et f(t)=e^{-0.2t}.

  1. En utilisant la propriété ci-dessus, faire le tableau de variations de la fonction f.
correction variations de f

2. En utilisant la propriété ci-dessus, faire le tableau de variations de la fonction g.

correction variations de g

3. Associer à chaque courbe sa fonction.

correction associer courbe et fonction

Exercice n°9 

On cherche à prévoir l’évolution de l’audience d’une chaîne de télévision lors des
dix prochaines années.
On considère que le nombre journalier (exprimé en milliers) de téléspectateurs de la chaîne est
modélisé par la fonction f définie sur l’intervalle [0;29] par 

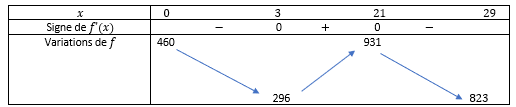
 f (x) = (20x^2 −80x +460) e^{-0.1x}
où x représente le nombre d’années depuis 2000 (par exemple x=19 pour l’année 2019).
1. Donner une valeur approchée au millier du nombre de téléspectateurs de la chaîne le 1er
janvier 2014.

correction

2. On note f'(x) la fonction dérivée de fsur l’intervalle [0;29].
a. Démontrer que f'(x) = (−2x^2 +48x −126) e^{-0.1x}.

correction

b. On considère l’équation : −2x^2 +48x −126 = 0.
Un logiciel de calcul formel donne

Instruction :

Résultat :

Solve (−2x^2 +48x −126 = 0)

3 et 21

Retrouver ce résultat par le calcul.

correction

c. En déduire le signe de f'(x) sur l’intervalle [0;29] et construire le tableau des variations de f sur l’intervalle [0;29]. Arrondir les éléments du tableau à l’unité.

correction

d. Le nombre journalier de téléspectateurs de cette chaîne de télévision dépassera-t-il la
barre du million avant l’année 2029 ? Justifier

correction

©2020 – Math’O karé SAS

f(x)= exp(x)+x^2+1 pour x\in \mathbf{R}

On veut calculer f'(x).

On répond à la question suivante : f(x) est-elle une somme, le produit d’un réel par une fonction, le produit de deux fonctions, l’inverse d’une fonction ou le quotient de deux fonctions ?

C’est la somme de trois termes :

exp(x) , x^2 et 1.

La dérivée d’une somme est la somme des dérivées d’après le tableau n°1 ci-dessous

f(x) est 

f'(x) se calcule ainsi :

une somme u+v

u’+v’

le produit d’une constante k par une fonction u c’est-à-dire ku

k\times u’

un produit de deux fonctions u\times v

u’\times v+u\times v’

l’inverse d’une fonction \frac{1}{u}

-\frac{u’}{u^2}

un quotient \frac{u}{v}

 \frac{u’\times v-u\times v’}{v^2}

Il faut donc calculer les dérivées des trois termes exp(x) , x^2 et 1 en utilisant le deuxième tableau et le cas échéant le premier tableau.

Je calcule la dérivée de x^2 

C’est une fonction de référence, j‘utilise la ligne carré du deuxième tableau.

(x^2)’=2x

 

Je calcule la dérivée de exp(x) 

C’est une fonction de référence, j‘utilise la ligne exponentielle du deuxième tableau. La notation utilisée est e^x qui sera introduite plus tard.

(exp(x))’=exp(x)

Je calcule la dérivée de 1 .

C’est une fonction de référence , j’utilise la ligne constante du tableau ci-dessous).

(1)’=0

Fonction

f(x)

Dérivable sur…

f'(x)

constante

f(x)=k\mathbf{R}f'(x)=0

identité

f(x)=x\mathbf{R}f'(x)=1

carré

f(x)=x^2\mathbf{R}f'(x)=2x

cube

f(x)=x^3\mathbf{R}f'(x)=3x^2

inverse 

f(x)=\frac{1}{x}\left]-\infty;0\right[\cup\left]0;+\infty\right[f'(x)=-\frac{1}{x^2}

racine carrée

f(x)=\sqrt{x}]0;+\infty[f'(x)=\frac{1}{2\sqrt{x}}
exponentiellef(x)=e^x\mathbf{R}f'(x)=e^x

Voilà ce qu’il faut écrire sur votre copie (dans cette correction, il y a toutes les étapes de calculs pour que chacun de mes abonnés puisse la comprendre)

f'(x)= (exp(x)+x^2+1)’\\\hspace{0.9cm}=(exp(x))’+(x^2)’+(1)’\\\hspace{0.9cm}= exp(x)+2x+0\\\hspace{0.9cm}= exp(x)+2x

 

f(x)= x^2\times exp(x) pour x\in \mathbf{R}

1.On veut calculer f'(x).

On répond à la question suivante : f(x) est-elle une somme, le produit d’un réel par une fonction, le produit de deux fonctions, l’inverse d’une fonction ou le quotient de deux fonctions ?

C’est le produit de deux fonctions u\times v avec  u(x)=x^2 et v(x)=exp(x).

On va utiliser la ligne n°3 du tableau n°1 ci-dessous.

f(x) est 

f'(x) se calcule ainsi :

une somme u+v

u’+v’

le produit d’une constante k par une fonction u c’est-à-dire ku

k\times u’

un produit de deux fonctions u\times v

u’\times v+u\times v’

l’inverse d’une fonction \frac{1}{u}

-\frac{u’}{u^2}

un quotient \frac{u}{v}

 \frac{u’\times v-u\times v’}{v^2}

2a.on veut calculer la dérivée  u'(x)

u(x)=x^2 est une fonction de référence, on utilise la  ligne carré du tableau n°2 ci-dessous

u'(x)=2x 

2b.on veut calculer la dérivée  v'(x)

v(x)=exp(x)est une fonction de référence, on utilise la ligne exponentielle du tableau n°2 ci-dessous

 v'(x)=exp(x) 

Fonction

f(x)

Dérivable sur…

f'(x)

constante

f(x)=k\mathbf{R}f'(x)=0

identité

f(x)=x\mathbf{R}f'(x)=1

carré

f(x)=x^2\mathbf{R}f'(x)=2x

cube

f(x)=x^3\mathbf{R}f'(x)=3x^2

inverse 

f(x)=\frac{1}{x}\left]-\infty;0\right[\cup\left]0;+\infty\right[f'(x)=-\frac{1}{x^2}

racine carrée

f(x)=\sqrt{x}]0;+\infty[f'(x)=\frac{1}{2\sqrt{x}}
exponentiellef(x)=e^x\mathbf{R}f'(x)=e^x

3. On calcule la dérivée f'(x) 

On remplace u par  x^2,  v par exp(x), u’ par  2x et v’ par exp(x) dans la formule u’\times v+u\times v’ 

Voilà ce qu’il faut écrire sur votre copie :

f'(x)= (x^2\times exp(x))’\\f'(x)=(x^2)’\times{exp(x)}+x^2\times{(exp(x))’} \\f'(x)=2x\times {exp(x)}+{x^2}\times{exp(x)}

 

f(x)= \frac{exp(x)+1}{x^2+1} pour x\in \mathbf{R} .

1.On veut calculer f'(x).

On répond à la question suivante : f(x) est-elle une somme, le produit d’un réel par une fonction, le produit de deux fonctions, l’inverse d’une fonction ou le quotient de deux fonctions ?

C’est le quotient de deux fonctions \frac{u}{ v} avec  u(x)=exp(x)+1 et v(x)=x^2+1.

On va utiliser la ligne n°5 du tableau n°1 ci-dessous.

f(x) est 

f'(x) se calcule ainsi :

une somme u+v

u’+v’

le produit d’une constante k par une fonction u c’est-à-dire ku

k\times u’

un produit de deux fonctions u\times v

u’\times v+u\times v’

l’inverse d’une fonction \frac{1}{u}

-\frac{u’}{u^2}

un quotient \frac{u}{v}

 \frac{u’\times v-u\times v’}{v^2}

2a.on veut calculer la dérivée  u'(x)

u(x)=exp(x)+1 est une  somme, on utilise la 1ère ligne du tableau n°1 

u'(x)=(exp(x)+1)’

u'(x)=(exp(x))’+(1)’

On utilise la première ligne (constante) et la dernière (exponentielle) du tableau 2 ci-dessous pour finir le calcul.

u'(x)=exp(x)+0

u'(x)=exp(x)

2b.on veut calculer la dérivée  v'(x)

v(x)=x^2+1 est une somme, on utilise la 1ère ligne du tableau n°1 

v'(x)=(x^2+1)’

v'(x)=(x^2)’+(1)’

On utilise les lignes 1 (constante) et 3 (carré) du tableau 2 ci-dessous pour finir le calcul.

v'(x)=2x+0

v'(x)=2x

Fonction

f(x)

Dérivable sur…

f'(x)

constante

f(x)=k\mathbf{R}f'(x)=0

identité

f(x)=x\mathbf{R}f'(x)=1

carré

f(x)=x^2\mathbf{R}f'(x)=2x

cube

f(x)=x^3\mathbf{R}f'(x)=3x^2

inverse 

f(x)=\frac{1}{x}\left]-\infty;0\right[\cup\left]0;+\infty\right[f'(x)=-\frac{1}{x^2}

racine carrée

f(x)=\sqrt{x}]0;+\infty[f'(x)=\frac{1}{2\sqrt{x}}
exponentiellef(x)=e^x\mathbf{R}f'(x)=e^x

3. On calcule la dérivée f'(x) 

On remplace u par  exp(x)+1,  v par x^2+1, u’ par  exp(x) et v’ par 2x dans la formule \frac{u’\times v-u\times v’}{v^2} 

Voilà ce qu’il faut écrire sur votre copie :

f'(x)= (\frac{exp(x)+1}{x^2+1})’\\f'(x)=\frac{(exp(x)+1)’\times{(x^2+1)}-{(exp(x)+1)}\times{(x^2+1)’}}{(x^2+1)^2}\\f'(x)=\frac{exp(x)\times{(x^2+1)}-{(exp(x)+1)}\times{2x}}{(x^2+1)^2}

On développe les deux produits au numérateur. Petit conseil, pour éviter les erreurs de signe laisser le deuxième développement entre parenthèses.

 f'(x)=\frac{exp(x)\times x^2+exp(x)-(exp(x)\times 2x +2x)}{(x^2+1)^2} 

Enlever les parenthèses. Attention il y a un signe moins devant, on change le signe de ce qu’il y a entre parenthèses.

 f'(x)=\frac{x^2exp(x)+exp(x)-2xexp(x) -2x}{(x^2+1)^2} 

 

On utilise la propriété:

exp(x)\times exp(y)=exp(x+y)

exp(3x-1)\times exp(2-2x)=exp(3x-1+2-2x)\\\hspace{4.1cm}=exp(x+1)

On utilise la propriété:

exp(x)\times exp(y)=exp(x+y)

(exp(2x+1))^2=exp(2x+1)\times exp(2x+1)\\\hspace{2.3cm}=exp(2x+1+2x+1)\\\hspace{2.3cm}=exp(4x+2)

On utilise la propriété:

exp(x)\times exp(y)=exp(x+y)

exp(2-6x)\times exp(12+6x)=exp(2-6x+12+6x)\\\hspace{4.3cm}=exp(14)

D’abord on développe

exp(-x)(exp(x)+1)=exp(-x)\times exp(x)+exp(-x)\times 1

On utilise la propriété:

exp(x)\times exp(y)=exp(x+y)

exp(-x)(exp(x)+1)=exp(-x+x)) +exp(-x) \\\hspace{3.3cm}=exp(0) +exp(-x)

Comme exp(0)=1, on peut remplacer exp(0) par 1 dans l’égalité ci-dessus.

\hspace{3.3cm}=1+exp(-x)

On utilise la propriété:

exp(x)\times exp(y)=exp(x+y)

exp(x+1)\times exp(x-1)=exp(x+1+x-1)\\\hspace{3.8cm}=exp(2x)

On utilise la propriété:

exp(x)\times exp(y)=exp(x+y)

exp(1+3x)\times exp(2-3x)=exp(1+3x+2-3x)\\\hspace{4.1cm}=exp(3)

On veut montrer que exp(-x)=\frac{1}{exp(x)}.

On va calculer exp(-x)\times{exp(x)} et en déduire que  exp(-x)=\frac{1}{exp(x)}.

On utilise la propriété précédente exp(x)\times exp(y)=exp(x+y)

exp(-x)\times{exp(x)}=exp(-x+x)

exp(-x)\times{exp(x)}=exp(0)

On utilise le fait que exp(0)=1

exp(-x)\times{exp(x)}=1

On divise de chaque côté par exp(x)

exp(-x)=\frac{1}{exp(x)}

 

Pour montrer l’égalité suivante : exp(x-y)=\frac{exp(x)}{exp(y)}, on part du membre de gauche pour arriver au membre de droite.

exp(x-y)=exp(x+(-y))

On utilise la propriété précédente exp(x+y)=exp(x)\times exp(y)

\hspace{1.7cm}=exp(x)\times exp(-y))

On utilise la propriété suivante exp(-y)=\frac{1}{ exp(y)}

\hspace{1.7cm}=exp(x)\times \frac{1}{ exp(y)})

\hspace{1.7cm}=\frac{exp(x)}{ exp(y)})

 

\frac{exp(2x-1)}{exp(x+1)}est de la forme \frac{exp(a)}{exp(b)} avec a=2x-1 et b=x+1.

On va utiliser la propriété : \frac{exp(a)}{exp(b)}=exp(a-b) en remplaçant a par 2x-1 et b par x+1.

\frac{exp(2x-1)}{exp(x+1)}=exp((2x-1)-(x+1))

\hspace{1.4cm}=exp(2x-1-x-1)

\hspace{1.4cm}=exp(x-2)

\frac{exp(3x)}{exp(2x+1)}est de la forme \frac{exp(a)}{exp(b)} avec a=3x et b=2x+1.

On va utiliser la propriété : \frac{exp(a)}{exp(b)}=exp(a-b) en remplaçant a par 3x et b par 2x+1.

\frac{exp(3x)}{exp(2x+1)}=exp(3x-(2x+1))

\hspace{1.4cm}=exp(3x–2x-1)

\hspace{1.4cm}=exp(x-1)

\frac{exp(x)}{exp(5x+5)} est de la forme \frac{exp(a)}{exp(b)} avec a=x et b=5x+5.

On va utiliser la propriété : \frac{exp(a)}{exp(b)}=exp(a-b) en remplaçant a par x et b par 5x+5.

\frac{exp(x)}{exp(5x+5)}=exp(x-(5x+5))

\hspace{1.4cm}=exp(x-5x-5)

\hspace{1.4cm}=exp(-4x-5)

\frac{exp(5x+3)\times exp(2x-1)}{exp(2x+1)} n’est pas de la forme \frac{exp(a)}{exp(b)}, on va d’abord modifier le numérateur en appliquant une autre propriété du cours.

\frac{exp(5x+3)\times exp(2x-1)}{exp(2x+1)}=\frac{exp(5x+3+2x-1)}{exp(2x+1)}

\hspace{2.7cm}=\frac{exp(7x+2)}{exp(2x+1)}

\frac{exp(7x+2)}{exp(2x+1)}est de la forme \frac{exp(a)}{exp(b)} avec a=7x+2 et b=2x+1.

On va utiliser la propriété : \frac{exp(a)}{exp(b)}=exp(a-b) en remplaçant a par 7x+2 et b par 2x+1.

\frac{exp(7x+2)}{exp(2x+1)}=exp((7x+2)-(2x+1))

\hspace{1.4cm}=exp(7x+2-2x-1)

\hspace{1.4cm}=exp(5x+1)

 

\frac{exp(1+x)\times exp(1-x)}{exp(2)} n’est pas de la forme \frac{exp(a)}{exp(b)}, on va d’abord modifier le numérateur en appliquant une autre propriété du cours.

\frac{exp(1+x)\times exp(1-x)}{exp(2)}=\frac{exp(1+x+1-x)}{exp(2)}

\hspace{2.4cm}=\frac{exp(2)}{exp(2)}

\hspace{2.4cm}=1

 

\frac{exp(2x-1)\times exp(2x+1)}{exp(2x)} n’est pas de la forme \frac{exp(a)}{exp(b)}, on va d’abord modifier le numérateur en appliquant une autre propriété du cours.

\frac{exp(2x+1)\times exp(2x-1)}{exp(2x)}=\frac{exp(2x+1+2x-1)}{exp(2x)}

\hspace{2.7cm}=\frac{exp(4x)}{exp(2x)}

\hspace{2.7cm}=exp(4x-2x)

\hspace{2.7cm}=exp(2x)

 

On veut résoudre e^{x+1}=e^{2x+3}.

Pour cela il faut se ramener à une égalité du type e^{a}=e^b et appliquer la propriété e^{a}=e^b \iff a=b.

Ici e^{x+1}=e^{2x+3}est déjà sous la forme e^{a}=e^b avec a=x+1 et b=2x+3.

On va résoudre a=b.

x+1=2x+3 est une équation du premier degré, on remet à leur place les membres qui ne sont pas à leur place.

x-2x=3-1\\-x=2\\x=-2

La solution de l’équation est -2.

On veut résoudre e^{x^2}=e^{2x-1}.

Pour cela il faut se ramener à une égalité du type e^{a}=e^b et appliquer la propriété

e^{a}=e^b \iff a=b.

Ici e^{x^2}=e^{2x-1} est déjà sous la forme e^{a}=e^b avec a=x^2 et b=2x-1.

On va résoudre a=b.

x^2=2x-1 est une équation du second degré, je fais apparaître zéro à droite en enlevant 2x-1 de chaque côté.

x^2-2x+1=0

 L’équation x^2-2x+1=0 est de la forme ax^2+bx+c=0.

J’identifie les coefficients l’équation a=1, b=-2 et c=1.

Je calcule \Delta=b²-4ac  en remplaçant a,b,c  par 1,(- 2), 1  .

\Delta=(-2)²-4\times 1\times 1\\\Delta=4-4\\\Delta=0

comme \Delta=0 , l’équation admet une solution réelle notée x_0=-\frac{b}{2a} .

Je calcule x_0=-\frac{b}{2a} en remplaçant a,b  par 1, (-2).

x_0=-\frac{(-2)}{2\times 1}\\x_0=-\frac{(-2)}{2}\\x_0=1

La solution de l’équation est 1.

 

On veut résoudre \frac{e^{5x+1}}{e^{-4x+10}}=1.

Pour cela il faut se ramener à une égalité du type e^{a}=e^b.

On multiplie de chaque côté par e^{-4x+10}.

e^{5x+1}=e^{-4x+10}

Puis appliquer la propriété e^{a}=e^b \iff a=b.

Ici  e^{5x+1}=e^{-4x+10}   est déjà sous la forme e^{a}=e^b avec a=5x+1 et b=-4x+10.

On va résoudre a=b.

5x+1=-4x+10 est une équation du premier degré, on remet à leur place les membres qui ne sont pas à leur place.

5x+4x=10-1\\9x=9\\x=\frac{9}{9}\\x=1

La solution de l’équation est 1.

 

On veut résoudre e^{2x-1}=e.

Pour cela il faut se ramener à une égalité du type e^{a}=e^b

e^{2x-1}=e^1

Puis appliquer la propriété e^{a}=e^b \iff a=b.

Ici e^{2x-1}=e^1 est  sous la forme e^{a}=e^b avec a=2x-1 et b=1.

On va résoudre a=b.

2x-1=1 est une équation du premier degré, on remet à leur place les membres qui ne sont pas à leur place.

2x=1+1\\2x=2\\x=\frac{2}{2}\\x=1

La solution de l’équation est 1.

 

On veut résoudre e^{x^2+x+1}=1.

Pour cela il faut se ramener à une égalité du type e^{a}=e^b

e^{x^2+x+1}=e^0

Puis appliquer la propriété

e^{a}=e^b \iff a=b.

e^{x^2+x+1}=e^{0} est  sous la forme e^{a}=e^b avec a=x^2+x+1 et b=0.

On va résoudre a=b.

x^2+x+1=0 est une équation du second degré.

 L’équation x^2+x+1=0 est de la forme ax^2+bx+c=0.

J’identifie les coefficients l’équation a=1, b=1 et c=1.

Je calcule \Delta=b²-4ac  en remplaçant a,b,c  par 1,1, 1  .

\Delta=1²-4\times 1\times 1\\\Delta=1-4\\\Delta=-3

comme \Delta<0 , l’équation n’admet pas de solution réelle .

 

On veut résoudre {e^{2x+2}}\times{e^{4x+10}}=e.

Pour cela il faut se ramener à une égalité du type e^{a}=e^b.

On réduit {e^{2x+2}}\times{e^{4x+10}} avec une propriété du cours {e^{x}}\times{e^{y}}=e^{x+y}. De plus e=e^1.

e^{2x+2+4x+10}=e^1\\e^{6x+12}=e^1

Puis appliquer la propriété e^{a}=e^b \iff a=b.

e^{6x+12}=e^1  est sous la forme e^{a}=e^b avec a=6x+12 et b=1.

On va résoudre a=b.

6x+12=1 est une équation du premier degré, on remet à leur place les membres qui ne sont pas à leur place.

6x=1-12\\6x=-11\\x=-\frac{11}{6}

La solution de l’équation est -\frac{11}{6}.

 

On veut résoudre e^{5x-3}>e^{2x+3} 

Pour cela il faut se ramener à une inégalité du type e^{a}>e^b et utiliser le fait que la fonction exponentielle esr croissante ce qui signifie que les nombres et les images varient dans le même sens :  e^{a}>e^b \iff a>b.

Ici e^{5x-3}>e^{2x+3} est déjà sous la forme e^{a}>e^b avec a=5x-3 et b=2x+3.

On va résoudre a>b.

5x-3>2x+3 est une inéquation du premier degré, on remet à leur place les membres qui ne sont pas à leur place.

5x-2x>3+3\\3x>6

On divise par 3 qui est positif donc l’inégalité ne change pas de sens.

x>\frac{6}{3}\\x>2

L’ensemble solution  de l’inéquation est ]2;+\infty[.

 

 

On veut résoudre e^{x^2}\leq e^{3x-2} 

Pour cela il faut se ramener à une inégalité du type e^{a}\leq e^b et utiliser le fait que la fonction exponentielle esr croissante ce qui signifie que les nombres et les images varient dans le même sens :  e^{a}\leq e^b \iff a\leq b.

Ici e^{x^2}\leq e^{3x-2} est déjà sous la forme e^{a}\leq e^b avec a=x^2 et b=3x-2.

On va résoudre a\leq b.

x^2 \leq 3x-2 est une inéquation du second degré, on fait apparaître le zéro à droite en enlevant 3x-2 de chaque côté.

x^2-3x+2 \leq 0

Etape n°1 : Ecrire la phrase d’introduction.

Je cherche pour quelles valeurs de x le polynôme x^2-3x+2 est de signe négatif (–) ou nul (0)

Etape n°2: Etude du signe de x^2-3x+2 par le calcul.

J’identifie les coefficients l’équation a=1, b=-3 et c=2.

Je calcule \Delta=b²-4ac  en remplaçant a,b,c  par 1, (-3) ,2  .

\Delta=(-3)²-4\times{1}\times{2}\\\Delta=9-8\\\Delta=1

Comme \Delta>0 , l’équation admet deux solutions réelles notées

x_1=\frac{-b-\sqrt{\Delta}}{2a} et x_2=\frac{-b+\sqrt{\Delta}}{2a}.

ax²+bx+c est  du signe de a à l’extérieur des racines et du signe de (-a) à l’intérieur des racines.

Je calcule x_1=\frac{-b-\sqrt{\Delta}}{2a} en remplaçant a,b,\Delta  par 1, (-3), 1.

x_1=\frac{-(-3)-\sqrt{1}}{2\times{1}}\\x_1=\frac{3-1}{2}\\x_1=\frac{2}{2}.

x_1=1.

Je calcule x_2=\frac{-b+\sqrt{\Delta}}{2a} en remplaçant a,b,\Delta  par 1, (-3),1.

x_2=\frac{-(-3)+\sqrt{1}}{2\times{1}}\\x_2=\frac{3+1}{2}\\x_2=\frac{4}{2}.

x_2=2.

Je dresse le tableau de signes du polynôme:

Comme a=1 le signe de a est positif.

Etape n°3 : Je réponds à la question posée en lisant le tableau de signes

le polynôme x^2-3x+2 est de signe négatif (–) ou nul (0) pour la deuxième colonne du tableau de signes.

J’écris l’ensemble solution sous forme d’intervalle.

S=\left[1;2\right].

 

\frac{e^{2x+2}}{e^{-3x-13}}\geq 1

Pour cela il faut se ramener à une inégalité du type e^{a}\geq e^b 

On multiplie par e^{-3x-13} de chaque côté qui est positif donc l’inégalité ne change pas de sens.

e^{2x+2}\geq e^{-3x-13}

Puis utiliser le fait que la fonction exponentielle esr croissante ce qui signifie que les nombres et les images varient dans le même sens :  e^{a}\geq e^b \iff a\geq b.

e^{2x+2}\geq e^{-3x-13}  est  sous la forme e^{a}\geq e^b avec a=2x+2 et b=-3x-13.

On va résoudre a\geq b.

2x+2\geq -3x-13 est une inéquation du premier degré, on remet à leur place les membres qui ne sont pas à leur place.

2x+3x\geq -13-2\\5x\geq -15

On divise par 5 qui est positif donc l’inégalité ne change pas de sens.

x\geq -\frac{15}{5}\\x\geq -3

L’ensemble solution  de l’inéquation est ]-3;+\infty [.

On veut résoudre e^{6x-5}>e 

Pour cela il faut se ramener à une inégalité du type e^{a}>e^b. On remplace e par e^1.

e^{6x-5}>e^1

Puis utiliser le fait que la fonction exponentielle esr croissante ce qui signifie que les nombres et les images varient dans le même sens :  e^{a}>e^b \iff a>b.

e^{6x-5}>e^{1} est de la forme e^{a}>e^b avec a=6x-5 et b=1.

On va résoudre a>b.

6x-5>1 est une inéquation du premier degré, on remet à leur place les membres qui ne sont pas à leur place.

6x>1+5\\6x>6

On divise par 6 qui est positif donc l’inégalité ne change pas de sens.

x>\frac{6}{6}\\x>1

L’ensemble solution  de l’inéquation est ]1;+\infty[.

 

On veut résoudre e^{x^2+4x+4}>1 

Pour cela il faut se ramener à une inégalité du type e^{a}>e^b. On remplace 1 par e^0.

e^{x^2+4x+4}>e^0

Puis utiliser le fait que la fonction exponentielle esr croissante ce qui signifie que les nombres et les images varient dans le même sens :  e^{a}>e^b \iff a>b.

e^{x^2+4x+4}>e^0 est de la forme e^{a}>e^b avec a=x^2+4x+4 et b=0.

On va résoudre a>b.

x^2+4x+4>0 est une inéquation du second degré.

Etape n°1 : Ecrire la phrase d’introduction.

Je cherche pour quelles valeurs de x le polynôme x^2+4x+4 est de signe positif (+).

Etape n°2: Etude du signe de x^2+4x+4 par le calcul.

J’identifie les coefficients du polynôme a=1, b=4 et c=4.

Je calcule \Delta=b²-4ac  en remplaçant a,b,c  par 1, 4, 4  .

\Delta=4²-4\times{1}\times{4}\\\Delta=16-16\\\Delta=0

comme  \Delta=0, ax²+bx+c est toujours du signe de a et s’annule pour x_0=-\frac{b}{2a}

Je calcule x_0=-\frac{b}{2a} en remplaçant a,b  par 1, 4.

x_0=-\frac{4}{2\times{1}}\\x_0=-2

Je dresse le tableau de signes du polynôme:

Comme a=1 le signe de a est positif.

Etape n°3 : Je réponds à la question posée en lisant le tableau de signes

le polynôme x^2+4x+1 est de signe positif (+)   pour toutes les valeurs de x sauf -2  .

J’écris l’ensemble solution sous forme de la réunion de deux intervalles.

S=]-\infty;-2[\cup]-2;+\infty[.

 

{e^{x-2}}\times{e^{3x+1}}\leq e

Pour cela il faut se ramener à une inégalité du type e^{a}\leq e^b 

On transforme {e^{x-2}}\times{e^{3x+1}}\leq e  à l’aide de {e^{x}}\times{e^{y}}= e^{x+y}  et on remplace e par e^{1}.

e^{x-2+3x+1}\leq e^{1}\\e^{4x-1}\leq e^{1}

Puis utiliser le fait que la fonction exponentielle esr croissante ce qui signifie que les nombres et les images varient dans le même sens :  e^{a}\leq e^b \iff a\leq b.

e^{4x-1}\leq e^{1}  est  sous la forme e^{a}\leq e^b avec a=4x-1 et b=1.

On va résoudre a\leq b.

4x-1\leq 1 est une inéquation du premier degré, on remet à leur place les membres qui ne sont pas à leur place.

4x\leq 1+1\\4x\leq 2

On divise par 4 qui est positif donc l’inégalité ne change pas de sens.

x\leq \frac{2}{4}\\x\leq \frac{1}{2}

L’ensemble solution  de l’inéquation est ]-\infty;\frac{1}{2} [.

f(x)= e^x-5 pour x\in \mathbf{R}

On veut calculer f'(x).

On répond à la question suivante : f(x) est-elle une somme, le produit d’un réel par une fonction, le produit de deux fonctions, l’inverse d’une fonction ou le quotient de deux fonctions ?

C’est la somme de deux termes :

e^x et -5.

La dérivée d’une somme est la somme des dérivées d’après le tableau n°1 ci-dessous

f(x) est 

f'(x) se calcule ainsi :

une somme u+v

u’+v’

le produit d’une constante k par une fonction u c’est-à-dire ku

k\times u’

un produit de deux fonctions u\times v

u’\times v+u\times v’

l’inverse d’une fonction \frac{1}{u}

-\frac{u’}{u^2}

un quotient \frac{u}{v}

 \frac{u’\times v-u\times v’}{v^2}

Il faut donc calculer les dérivées des deux termes e^x et -5 en utilisant le deuxième tableau et le cas échéant le premier tableau.

Je calcule la dérivée de e^x 

C’est une fonction de référence, j‘utilise la ligne exponentielle du deuxième tableau.

(e^x)’=e^x

Je calcule la dérivée de -5 .

C’est une fonction de référence , j’utilise la ligne constante du tableau ci-dessous).

(-5)’=0

Fonction

f(x)

Dérivable sur…

f'(x)

constante

f(x)=k\mathbf{R}f'(x)=0

identité

f(x)=x\mathbf{R}f'(x)=1

carré

f(x)=x^2\mathbf{R}f'(x)=2x

cube

f(x)=x^3\mathbf{R}f'(x)=3x^2

inverse 

f(x)=\frac{1}{x}\left]-\infty;0\right[\cup\left]0;+\infty\right[f'(x)=-\frac{1}{x^2}

racine carrée

f(x)=\sqrt{x}]0;+\infty[f'(x)=\frac{1}{2\sqrt{x}}
exponentiellef(x)=e^x\mathbf{R}f'(x)=e^x

Voilà ce qu’il faut écrire sur votre copie (dans cette correction, il y a toutes les étapes de calculs pour que chacun de mes abonnés puisse la comprendre)

f'(x)= (e^x-5)’\\\hspace{0.9cm}=(e^x)’-(5)’\\\hspace{0.9cm}= e^x-0\\\hspace{0.9cm}= e^x

f(x)= 3e^x+x^2 pour x\in \mathbf{R}

On veut calculer f'(x).

On répond à la question suivante : f(x) est-elle une somme, le produit d’un réel par une fonction, le produit de deux fonctions, l’inverse d’une fonction ou le quotient de deux fonctions ?

C’est la somme de deux termes :

3e^x et x^2.

La dérivée d’une somme est la somme des dérivées d’après le tableau n°1 ci-dessous

f(x) est 

f'(x) se calcule ainsi :

une somme u+v

u’+v’

le produit d’une constante k par une fonction u c’est-à-dire ku

k\times u’

un produit de deux fonctions u\times v

u’\times v+u\times v’

l’inverse d’une fonction \frac{1}{u}

-\frac{u’}{u^2}

un quotient \frac{u}{v}

 \frac{u’\times v-u\times v’}{v^2}

Il faut donc calculer les dérivées des deux termes 3e^x et x^2 en utilisant le deuxième tableau et le cas échéant le premier tableau.

Je calcule la dérivée de 3e^x 

J’utilise la ligne n°2 du tableau 1

(3e^x)’=3(e^x)’ 

e^x est une fonction de référence, j‘utilise la ligne exponentielle du deuxième tableau.

(3e^x)’=3e^x 

Je calcule la dérivée de x^2 .

C’est une fonction de référence , j’utilise la ligne carré du tableau ci-dessous).

(x^2)’=2x

Fonction

f(x)

Dérivable sur…

f'(x)

constante

f(x)=k\mathbf{R}f'(x)=0

identité

f(x)=x\mathbf{R}f'(x)=1

carré

f(x)=x^2\mathbf{R}f'(x)=2x

cube

f(x)=x^3\mathbf{R}f'(x)=3x^2

inverse 

f(x)=\frac{1}{x}\left]-\infty;0\right[\cup\left]0;+\infty\right[f'(x)=-\frac{1}{x^2}

racine carrée

f(x)=\sqrt{x}]0;+\infty[f'(x)=\frac{1}{2\sqrt{x}}
exponentiellef(x)=e^x\mathbf{R}f'(x)=e^x

Voilà ce qu’il faut écrire sur votre copie (dans cette correction, il y a toutes les étapes de calculs pour que chacun de mes abonnés puisse la comprendre)

f'(x)= (3e^x+x^2)’\\\hspace{0.9cm}=(3e^x)’+(x^2)’\\\hspace{0.9cm}= 3(e^x)’+2x\\\hspace{0.9cm}= 3e^x+2x

 

f(x)= x\times e^x pour x\in \mathbf{R}

1.On veut calculer f'(x).

On répond à la question suivante : f(x) est-elle une somme, le produit d’un réel par une fonction, le produit de deux fonctions, l’inverse d’une fonction ou le quotient de deux fonctions ?

C’est le produit de deux fonctions u\times v avec  u(x)=x et v(x)=e^x.

On va utiliser la ligne n°3 du tableau n°1 ci-dessous.

f(x) est 

f'(x) se calcule ainsi :

une somme u+v

u’+v’

le produit d’une constante k par une fonction u c’est-à-dire ku

k\times u’

un produit de deux fonctions u\times v

u’\times v+u\times v’

l’inverse d’une fonction \frac{1}{u}

-\frac{u’}{u^2}

un quotient \frac{u}{v}

 \frac{u’\times v-u\times v’}{v^2}

2a.on veut calculer la dérivée  u'(x)

u(x)=x est une fonction de référence, on utilise la  ligne identité du tableau n°2 ci-dessous

u'(x)=1 

2b.on veut calculer la dérivée  v'(x)

v(x)=e^xest une fonction de référence, on utilise la ligne exponentielle du tableau n°2 ci-dessous

 v'(x)=e^x 

Fonction

f(x)

Dérivable sur…

f'(x)

constante

f(x)=k\mathbf{R}f'(x)=0

identité

f(x)=x\mathbf{R}f'(x)=1

carré

f(x)=x^2\mathbf{R}f'(x)=2x

cube

f(x)=x^3\mathbf{R}f'(x)=3x^2

inverse 

f(x)=\frac{1}{x}\left]-\infty;0\right[\cup\left]0;+\infty\right[f'(x)=-\frac{1}{x^2}

racine carrée

f(x)=\sqrt{x}]0;+\infty[f'(x)=\frac{1}{2\sqrt{x}}
exponentiellef(x)=e^x\mathbf{R}f'(x)=e^x

3. On calcule la dérivée f'(x) 

On remplace u par  x,  v par e^x, u’ par  1 et v’ par e^x dans la formule u’\times v+u\times v’ 

Voilà ce qu’il faut écrire sur votre copie :

f'(x)= (x\times e^x)’\\f'(x)=(x)’\times{e^x}+x\times{(e^x)’} \\f'(x)=1\times {e^x}+{x}\times{e^x} \\f'(x)=e^x+xe^x

 

 

 

 

f(x)= e^x(2x+5) pour x\in \mathbf{R}

1.On veut calculer f'(x).

On répond à la question suivante : f(x) est-elle une somme, le produit d’un réel par une fonction, le produit de deux fonctions, l’inverse d’une fonction ou le quotient de deux fonctions ?

C’est le produit de deux fonctions u\times v avec  u(x)=e^x et v(x)=2x+5.

On va utiliser la ligne n°3 du tableau n°1 ci-dessous.

f(x) est 

f'(x) se calcule ainsi :

une somme u+v

u’+v’

le produit d’une constante k par une fonction u c’est-à-dire ku

k\times u’

un produit de deux fonctions u\times v

u’\times v+u\times v’

l’inverse d’une fonction \frac{1}{u}

-\frac{u’}{u^2}

un quotient \frac{u}{v}

 \frac{u’\times v-u\times v’}{v^2}

2a.on veut calculer la dérivée  u'(x)

u(x)=e^xest une fonction de référence, on utilise la ligne exponentielle du tableau n°2 ci-dessous

 u'(x)=e^x 

2b.on veut calculer la dérivée  v'(x)

v(x)=2x+5 est une somme, on utilise la ligne n°1 du tableau n°1

 v'(x)=(2x+5)’ 

 v'(x)=(2x)’+(5)’ 

 v'(x)=2(x)’+0 

 v'(x)=2\times 1 

 v'(x)=2 

Fonction

f(x)

Dérivable sur…

f'(x)

constante

f(x)=k\mathbf{R}f'(x)=0

identité

f(x)=x\mathbf{R}f'(x)=1

carré

f(x)=x^2\mathbf{R}f'(x)=2x

cube

f(x)=x^3\mathbf{R}f'(x)=3x^2

inverse 

f(x)=\frac{1}{x}\left]-\infty;0\right[\cup\left]0;+\infty\right[f'(x)=-\frac{1}{x^2}

racine carrée

f(x)=\sqrt{x}]0;+\infty[f'(x)=\frac{1}{2\sqrt{x}}
exponentiellef(x)=e^x\mathbf{R}f'(x)=e^x

3. On calcule la dérivée f'(x) 

On remplace u par  e^x,  v par 2x+5, u’ par  e^x et v’ par 2 dans la formule u’\times v+u\times v’ 

Voilà ce qu’il faut écrire sur votre copie :

f'(x)= (e^x(2x+5))’\\f'(x)=(e^x)’\times{(2x+5)}+e^x\times{(2x+5)’} \\f'(x)=e^x(2x+5)+e^x\times2 \\f'(x)=e^x(2x+5)+2e^x \\f'(x)=e^x(2x+5+2) \\f'(x)=e^x(2x+7)

 

f(x)= \frac{1}{e^x+10} pour x\in \mathbf{R} .

1.On veut calculer f'(x).

On répond à la question suivante : f(x) est-elle une somme, le produit d’un réel par une fonction, le produit de deux fonctions, l’inverse d’une fonction ou le quotient de deux fonctions ?

C’est l’inverse d’une fonction \frac{1}{ u} avec  u(x)=e^x+10.

On va utiliser la ligne n°4 du tableau n°1 ci-dessous.

f(x) est 

f'(x) se calcule ainsi :

une somme u+v

u’+v’

le produit d’une constante k par une fonction u c’est-à-dire ku

k\times u’

un produit de deux fonctions u\times v

u’\times v+u\times v’

l’inverse d’une fonction \frac{1}{u}

-\frac{u’}{u^2}

un quotient \frac{u}{v}

 \frac{u’\times v-u\times v’}{v^2}

2a.on veut calculer la dérivée  u'(x)

u(x)=e^x+10 est une  somme, on utilise la 1ère ligne du tableau n°1 

u'(x)=(e^x+10)’

u'(x)=(e^x)’+(10)’

On utilise la première ligne (constante) et la dernière (exponentielle) du tableau 2 ci-dessous pour finir le calcul.

u'(x)=e^x+0

u'(x)=e^x

Fonction

f(x)

Dérivable sur…

f'(x)

constante

f(x)=k\mathbf{R}f'(x)=0

identité

f(x)=x\mathbf{R}f'(x)=1

carré

f(x)=x^2\mathbf{R}f'(x)=2x

cube

f(x)=x^3\mathbf{R}f'(x)=3x^2

inverse 

f(x)=\frac{1}{x}\left]-\infty;0\right[\cup\left]0;+\infty\right[f'(x)=-\frac{1}{x^2}

racine carrée

f(x)=\sqrt{x}]0;+\infty[f'(x)=\frac{1}{2\sqrt{x}}
exponentiellef(x)=e^x\mathbf{R}f'(x)=e^x

3. On calcule la dérivée f'(x) 

On remplace u par  e^x+10, u’ par  e^x dans la formule -\frac{u’}{u^2} 

Voilà ce qu’il faut écrire sur votre copie :

f'(x)= (\frac{1}{e^x+10})’\\f'(x)=-\frac{(e^x+10)’}{(e^x+10)^2}\\f'(x)=-\frac{e^x}{(e^x+10)^2}

 

f(x)= \frac{e^x-5}{2e^x+3} pour x\in \mathbf{R} .

1.On veut calculer f'(x).

On répond à la question suivante : f(x) est-elle une somme, le produit d’un réel par une fonction, le produit de deux fonctions, l’inverse d’une fonction ou le quotient de deux fonctions ?

C’est le quotient de deux fonctions \frac{u}{ v} avec  u(x)=e^x-5 et v(x)=2e^x+3.

On va utiliser la ligne n°5 du tableau n°1 ci-dessous.

f(x) est 

f'(x) se calcule ainsi :

une somme u+v

u’+v’

le produit d’une constante k par une fonction u c’est-à-dire ku

k\times u’

un produit de deux fonctions u\times v

u’\times v+u\times v’

l’inverse d’une fonction \frac{1}{u}

-\frac{u’}{u^2}

un quotient \frac{u}{v}

 \frac{u’\times v-u\times v’}{v^2}

2a.on veut calculer la dérivée  u'(x)

u(x)=e^x-5 est une  somme, on utilise la 1ère ligne du tableau n°1 

u'(x)=(e^x-5)’

u'(x)=(e^x)’-(5)’

On utilise la première ligne (constante) et la dernière (exponentielle) du tableau 2 ci-dessous pour finir le calcul.

u'(x)=e^x-0

u'(x)=e^x

2b.on veut calculer la dérivée  v'(x)

v(x)=2e^x+3 est une  somme, on utilise la 1ère ligne du tableau n°1 

v'(x)=(2e^x+3)’

v'(x)=(2e^x)’+(3)’

on utilise la 2ème ligne du tableau n°1

v'(x)=2(e^x)’+(3)’

On utilise la première ligne (constante) et la dernière (exponentielle) du tableau 2 ci-dessous pour finir le calcul.

v'(x)=2e^x+0

v'(x)=2e^x

Fonction

f(x)

Dérivable sur…

f'(x)

constante

f(x)=k\mathbf{R}f'(x)=0

identité

f(x)=x\mathbf{R}f'(x)=1

carré

f(x)=x^2\mathbf{R}f'(x)=2x

cube

f(x)=x^3\mathbf{R}f'(x)=3x^2

inverse 

f(x)=\frac{1}{x}\left]-\infty;0\right[\cup\left]0;+\infty\right[f'(x)=-\frac{1}{x^2}

racine carrée

f(x)=\sqrt{x}]0;+\infty[f'(x)=\frac{1}{2\sqrt{x}}
exponentiellef(x)=e^x\mathbf{R}f'(x)=e^x

3. On calcule la dérivée f'(x) 

On remplace u par  e^x-5,  v par 2e^x+3, u’ par  e^x et v’ par 2e^x dans la formule \frac{u’\times v-u\times v’}{v^2} 

Voilà ce qu’il faut écrire sur votre copie :

f'(x)= (\frac{e^x-5}{2e^x+3})’\\f'(x)=\frac{(e^x-5)’\times{(2e^x+3)}-{(e^x-5)}\times{(2e^x+3)’}}{(2e^x+3)^2}\\f'(x)=\frac{e^x\times{(2e^x+3)}-{(e^x-5)}\times{2e^x}}{(2e^x+3)^2}

On développe les deux produits au numérateur. Petit conseil, pour éviter les erreurs de signe laisser le deuxième développement entre parenthèses.

 f'(x)=\frac{e^x\times 2e^x+3e^x-(e^x\times 2e^x -10e^x)}{(2e^x+3)^2} 

Enlever les parenthèses. Attention il y a un signe moins devant, on change le signe de ce qu’il y a entre parenthèses.

 f'(x)=\frac{e^x\times 2e^x+3e^x-e^x\times 2e^x +10e^x}{(2e^x+3)^2} 

On réduit le dénominateur

f'(x)=\frac{13e^x}{(2e^x+3)^2} 

 

  1. f(x)=e^{2x-4}+1 définie sur \mathbf{R}

On veut calculer f'(x).

On répond à la question suivante : f(x) est-elle une somme, le produit d’un réel par une fonction, le produit de deux fonctions, l’inverse d’une fonction ou le quotient de deux fonctions ?

C’est la somme de deux termes :

e^{2x-4}  et 1.

La dérivée d’une somme est la somme des dérivées d’après le tableau n°1 ci-dessous

f(x) est 

f'(x) se calcule ainsi :

une somme u+v

u’+v’

le produit d’une constante k par une fonction u c’est-à-dire ku

k\times u’

un produit de deux fonctions u\times v

u’\times v+u\times v’

l’inverse d’une fonction \frac{1}{u}

-\frac{u’}{u^2}

un quotient \frac{u}{v}

 \frac{u’\times v-u\times v’}{v^2}

Il faut donc calculer les dérivées des trois termes e^{2x-4} et 1 en utilisant le deuxième tableau et le cas échéant le premier tableau.

Je calcule la dérivée de e^{2x-4} 

C’est une fonction de référence, j‘utilise la dernière ligne du deuxième tableau. 

(e^{2x-4})’=2e^{2x-4}

Je calcule la dérivée de 1 .

C’est une fonction de référence , j’utilise la ligne constante du tableau ci-dessous).

(1)’=0

Fonction

f(x)

Dérivable sur…

f'(x)

constante

f(x)=k\mathbf{R}f'(x)=0

identité

f(x)=x\mathbf{R}f'(x)=1

carré

f(x)=x^2\mathbf{R}f'(x)=2x

cube

f(x)=x^3\mathbf{R}f'(x)=3x^2

inverse 

f(x)=\frac{1}{x}\left]-\infty;0\right[\cup\left]0;+\infty\right[f'(x)=-\frac{1}{x^2}

racine carrée

f(x)=\sqrt{x}]0;+\infty[f'(x)=\frac{1}{2\sqrt{x}}
exponentiellef(x)=e^x\mathbf{R}f'(x)=e^x
e^{ax+b}f(x)=e^{ax+b}\mathbf{R}f'(x)=ae^{ax+b}

Voilà ce qu’il faut écrire sur votre copie (dans cette correction, il y a toutes les étapes de calculs pour que chacun de mes abonnés puisse la comprendre)

f'(x)= (e^{2x-4}+1)’\\\hspace{0.9cm}=(e^{2x-4})’+(1)’\\\hspace{0.9cm}= 2e^{2x-4}+0\\\hspace{0.9cm}= 2e^{2x-4}

 

f(x)=xe^{0.1x+0.2} définie sur \mathbf{R}

1.On veut calculer f'(x).

On répond à la question suivante : f(x) est-elle une somme, le produit d’un réel par une fonction, le produit de deux fonctions, l’inverse d’une fonction ou le quotient de deux fonctions ?

C’est le produit de deux fonctions u\times v avec  u(x)=x et v(x)=e^{0.1x+0.2}.

On va utiliser la ligne n°3 du tableau n°1 ci-dessous.

f(x) est 

f'(x) se calcule ainsi :

une somme u+v

u’+v’

le produit d’une constante k par une fonction u c’est-à-dire ku

k\times u’

un produit de deux fonctions u\times v

u’\times v+u\times v’

l’inverse d’une fonction \frac{1}{u}

-\frac{u’}{u^2}

un quotient \frac{u}{v}

 \frac{u’\times v-u\times v’}{v^2}

2a.on veut calculer la dérivée  u'(x)

u(x)=x est une fonction de référence, on utilise la  ligne identité du tableau n°2 ci-dessous

u'(x)=1 

2b.on veut calculer la dérivée  v'(x)

v(x)=e^{0.1x+0.2}est une fonction de référence, on utilise la dernière ligne  du tableau n°2 ci-dessous

v'(x)=0.1e^{0.1x+0.2}

Fonction

f(x)

Dérivable sur…

f'(x)

constante

f(x)=k\mathbf{R}f'(x)=0

identité

f(x)=x\mathbf{R}f'(x)=1

carré

f(x)=x^2\mathbf{R}f'(x)=2x

cube

f(x)=x^3\mathbf{R}f'(x)=3x^2

inverse 

f(x)=\frac{1}{x}\left]-\infty;0\right[\cup\left]0;+\infty\right[f'(x)=-\frac{1}{x^2}

racine carrée

f(x)=\sqrt{x}]0;+\infty[f'(x)=\frac{1}{2\sqrt{x}}
exponentiellef(x)=e^x\mathbf{R}f'(x)=e^x
e^{ax+b}f(x)=e^{ax+b}\mathbf{R}f'(x)=ae^{ax+b}

3. On calcule la dérivée f'(x) 

On remplace u par  x,  v par e^{0.1x+0.2}, u’ par  1 et v’ par 0.1e^{0.1x+0.2} dans la formule u’\times v+u\times v’ 

Voilà ce qu’il faut écrire sur votre copie :

f'(x)=(x+e^{0.1x+0.2})’\\f'(x)=(x)’\times e^{0.1x+0.2}+x\times (e^{0.1x+0.2})’\\f'(x)=1\times e^{0.1x+0.2}+x\times 0.1e^{0.1x+0.2}\\f'(x)= e^{0.1x+0.2}+0.1x e^{0.1x+0.2}

On peut éventuellement continuer :

f'(x)= (1+0.1x)e^{0.1x+0.2}

 

f(x)=\frac{e^{2x}}{e^{2x}+1} définie sur \mathbf{R}

1.On veut calculer f'(x).

On répond à la question suivante : f(x) est-elle une somme, le produit d’un réel par une fonction, le produit de deux fonctions, l’inverse d’une fonction ou le quotient de deux fonctions ?

C’est le quotient de deux fonctions \frac{u}{ v} avec  u(x)=e^{2x} et v(x)=e^{2x}+1.

On va utiliser la ligne n°5 du tableau n°1 ci-dessous.

f(x) est 

f'(x) se calcule ainsi :

une somme u+v

u’+v’

le produit d’une constante k par une fonction u c’est-à-dire ku

k\times u’

un produit de deux fonctions u\times v

u’\times v+u\times v’

l’inverse d’une fonction \frac{1}{u}

-\frac{u’}{u^2}

un quotient \frac{u}{v}

 \frac{u’\times v-u\times v’}{v^2}

2a.on veut calculer la dérivée  u'(x)

u(x)=e^{2x} est une  fonction de référence, on utilise la dernière ligne du tableau n°2.

u'(x)=(e^{2x})’

u'(x)=2e^{2x}

 

2b.on veut calculer la dérivée  v'(x)

v(x)=e^{2x}+1 est une somme, on utilise la 1ère ligne du tableau n°1 

v'(x)=(e^{2x}+1)’

v'(x)=(e^{2x})’+(1)’

On utilise la ligne 1 (constante) et la dernière ligne du tableau 2 ci-dessous pour finir le calcul.

v'(x)=2e^{2x}+0

v'(x)=2e^{2x}

Fonction

f(x)

Dérivable sur…

f'(x)

constante

f(x)=k\mathbf{R}f'(x)=0

identité

f(x)=x\mathbf{R}f'(x)=1

carré

f(x)=x^2\mathbf{R}f'(x)=2x

cube

f(x)=x^3\mathbf{R}f'(x)=3x^2

inverse 

f(x)=\frac{1}{x}\left]-\infty;0\right[\cup\left]0;+\infty\right[f'(x)=-\frac{1}{x^2}

racine carrée

f(x)=\sqrt{x}]0;+\infty[f'(x)=\frac{1}{2\sqrt{x}}
exponentiellef(x)=e^x\mathbf{R}f'(x)=e^x
e^{ax+b}f(x)=e^{ax+b}\mathbf{R}f'(x)=ae^{ax+b}

3. On calcule la dérivée f'(x) 

On remplace u par  e^{2x},  v par e^{2x}+1, u’ par  2e^{2x} et v’ par 2e^{2x} dans la formule \frac{u’\times v-u\times v’}{v^2} 

Voilà ce qu’il faut écrire sur votre copie :

f'(x)= (\frac{e^{2x}}{x^2+1})’\\f'(x)=\frac{(e^{2x})’\times{(e^{2x}+1)}-{(e^{2x})}\times{(e^{2x}+1)’}}{(e^{2x}+1)^2}\\f'(x)=\frac{2e^{2x}\times{(e^{2x}+1)}-{(e^{2x})}\times{2e^{2x}}}{(e^{2x}+1)^2}

On développe les deux produits au numérateur. 

f'(x)=\frac{2e^{2x+2x}+2e^{2x}-2e^{2x+2x}}{(e^{2x}+1)^2}\\f'(x)=\frac{2e^{4x}+2e^{2x}-2e^{4x}}{(e^{2x}+1)^2}\\f'(x)=\frac{2e^{2x}}{(e^{2x}+1)^2}

 

f(t)=e^{0.5t}

C’est de la forme f(t)=e^{kt} avec k>0 donc f est croissante sur \mathbf{R}

La fonction f est croissante donc sa courbe est celle qui monte c’est-à-dire la courbe verte.

La fonction g est décroissante donc sa courbe est celle qui descend c’est-à-dire la courbe rouge.

Pour calculer le nombre de téléspectateurs en 2014 , il faut calculer f(14) en remplaçant tous les x  par 14 dans f(x)=(20x^2−80x+460)e^{−0,1x}.
f(14)=(20\times 14^2−80\times 14+460)e^{−0,1\times 14}

f(14)=803,906

Soit 804 milliers de téléspectateurs à un millier près.

f(x)= (20x^2-80x+460) e^{-0.1x}

1.On veut calculer f'(x).

On répond à la question suivante : f(x) est-elle une somme, le produit d’un réel par une fonction, le produit de deux fonctions, l’inverse d’une fonction ou le quotient de deux fonctions ?

C’est le produit de deux fonctions u\times v avec  u(x)=20x^2-80x+460 et v(x)=e^{-0.1x}.

On va utiliser la ligne n°3 du tableau n°1 ci-dessous.

f(x) est 

f'(x) se calcule ainsi :

une somme u+v

u’+v’

le produit d’une constante k par une fonction u c’est-à-dire ku

k\times u’

un produit de deux fonctions u\times v

u’\times v+u\times v’

l’inverse d’une fonction \frac{1}{u}

-\frac{u’}{u^2}

un quotient \frac{u}{v}

 \frac{u’\times v-u\times v’}{v^2}

2a.on veut calculer la dérivée  u'(x)

u(x)=20x^2-80x+460 est une somme, on utilise la  ligne n°1 du tableau n°1 ci-dessus

u'(x)=(20x^2-80x+460)’

u'(x)=(20x^2)’-(80x)’+(460)’

u'(x)=20(x^2)’-80(x)’+(460)’

u'(x)=20\times 2x-80\times 1+0

u'(x)=40x-80

2b.on veut calculer la dérivée  v'(x)

v(x)=e^{-0.1x} est une fonction de référence, on utilise la dernière ligne du tableau n°2 ci-dessous

v'(x)=-0.1e^{-0.1x}

Fonction

f(x)

Dérivable sur…

f'(x)

constante

f(x)=k\mathbf{R}f'(x)=0

identité

f(x)=x\mathbf{R}f'(x)=1

carré

f(x)=x^2\mathbf{R}f'(x)=2x

cube

f(x)=x^3\mathbf{R}f'(x)=3x^2

inverse 

f(x)=\frac{1}{x}\left]-\infty;0\right[\cup\left]0;+\infty\right[f'(x)=-\frac{1}{x^2}

racine carrée

f(x)=\sqrt{x}]0;+\infty[f'(x)=\frac{1}{2\sqrt{x}}
exponentiellef(x)=e^x\mathbf{R}f'(x)=e^x
e^{ax+b}f(x)=e^{ax+b}\mathbf{R}f'(x)=ae^{ax+b}

3. On calcule la dérivée f'(x) 

On remplace u par  20x^2-80x+460,  v par e^{-0.1x}, u’ par  40x-80 et v’ par -0.1e^{-0.1x} dans la formule u’\times v+u\times v’ 

Voilà ce qu’il faut écrire sur votre copie :

f'(x)= ((20x^2-80x+460) e^{-0.1x})’\\f'(x)=(20x^2-80x+460)’\times{e^{-0.1x}}+(20x^2-80x+460){(e^{-0.1x})’} \\f'(x)=(40x-80)\times {e^{-0.1x}}+{(20x^2-80x+460)}\times{(-0.1)e^{-0.1x}} \\f'(x)=(40x-80)\times {e^{-0.1x}}+{(-0.1\times20x^2+0.1\times80x-0.1\times460)}\times{e^{-0.1x}} \\f'(x)=(40x-80)\times {e^{-0.1x}}+{(-2x^2+8x-46)}\times{e^{-0.1x}}

On met e^{-0.1x} en facteur.

f'(x)=(40x-80-2x^2+8x-46)\times{e^{-0.1x}}\\f'(x)=(-2x^2+48x-126)\times{e^{-0.1x}}

 

 L’équation -2x^2+48x-126=0 est de la forme ax^2+bx+c=0

J’identifie les coefficients l’équation a=-2, b=48 et c=-126.

Je calcule \Delta=b²-4ac  en remplaçant a,b,c  par (-2), 48, (-126).

\Delta=48²-4\times{(-2)}\times{(-126)}\\\Delta=2304-1008\\\Delta=1296

comme \Delta>0 , l’équation admet deux solutions réelles notées

x_1=\frac{-b-\sqrt{\Delta}}{2a} et x_2=\frac{-b+\sqrt{\Delta}}{2a}

Je calcule x_1=\frac{-b-\sqrt{\Delta}}{2a} en remplaçant a,b,\Delta  par (-2) , 48  , 1296.

x_1=\frac{-48-\sqrt{1296}}{2\times{(-2)}}\\x_1=\frac{-48-36}{(-4)}\\x_1=\frac{-84}{(-4)}\\x_1=21

Je calcule x_2=\frac{-b+\sqrt{\Delta}}{2a} en remplaçant a,b,\Delta  par (-2), 48  , 1296.

x_2=\frac{-48+\sqrt{1296}}{2\times{(-2)}}\\x_2=\frac{-48+36}{(-4)}\\x_2=\frac{-12}{(-4)}\\x_2=3

Je conclus S=\{3;21\}

Ce qui correspond à ce qui est écrit dans l’énoncé.

 

On s’intéresse au signe de f'(x) sur l’intervalle [0;29].

f'(x)=(-2x^2+48x-126)e^{-0.1x}

Comme e^{-0.1x} est toujours positif, f'(x) est du signe de -2x^2+48x-126.

Dans la question précédente, on a calculé \Delta, il est positif donc -2x^2+48x-126 est du signe de a=-2 à l’extérieur des racines et du signe de -a=2 à l’intérieur des racines.

On construit le tableau des variations de f sur l’intervalle [0;29]. 

Pour déterminer les images de 0;3;21;29, mieux vaut utiliser la calculatrice TI 83 Premium ainsi :

 Le tableau de variations de la fonction f montre que le maximum de téléspectateurs est de 931 milliers en 2021 la barre du million ne sera jamais atteinte entre 2000 et 2029.

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.