1. Placer un point sur le cercle trigonométrique.

GEOMETRIE, Niveau première, Placer un point sur le cercle trigonométrique, Trigonométrie

Définition :

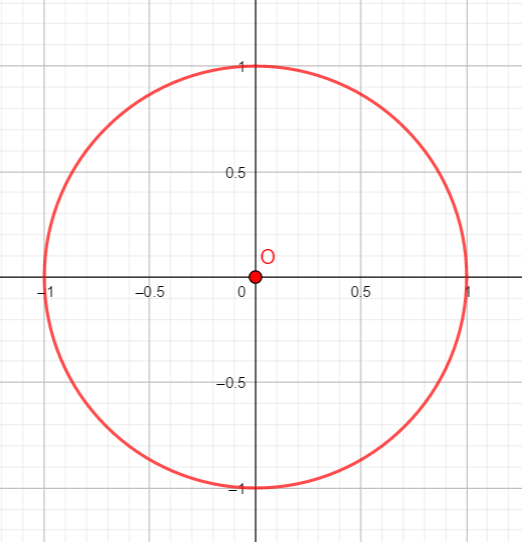
Le cercle trigonométrique de centre $O$ est celui qui a pour rayon $1$ et qui est muni du sens direct ( le sens contraire des aiguilles d’une montre).

Questions

Combien mesure la circonférence d’un cercle trigonométrique ?

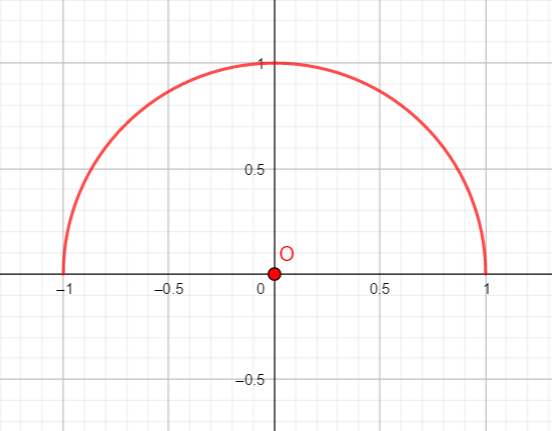
2. Combien mesure l’arc correspondant à un demi-cercle trigonométrique ?

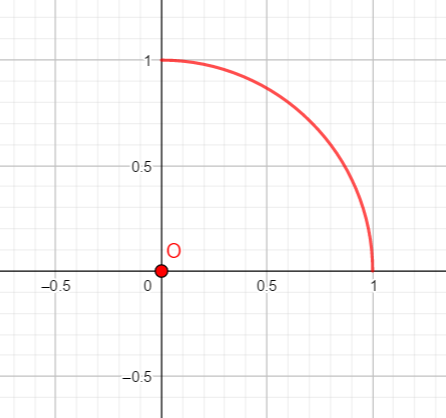
3. Combien mesure l’arc correspondant à un quart de cercle trigonométrique ?

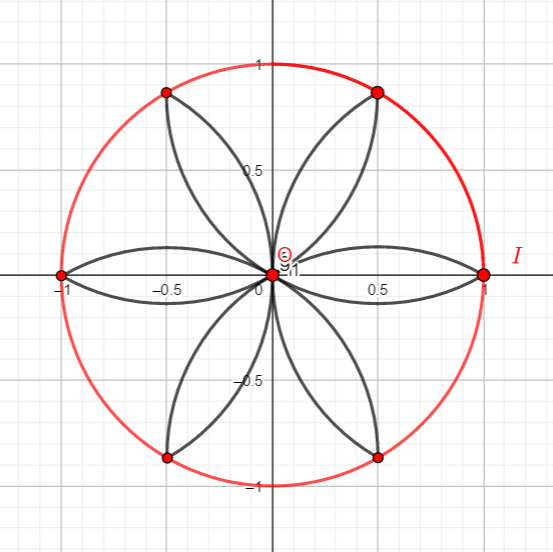
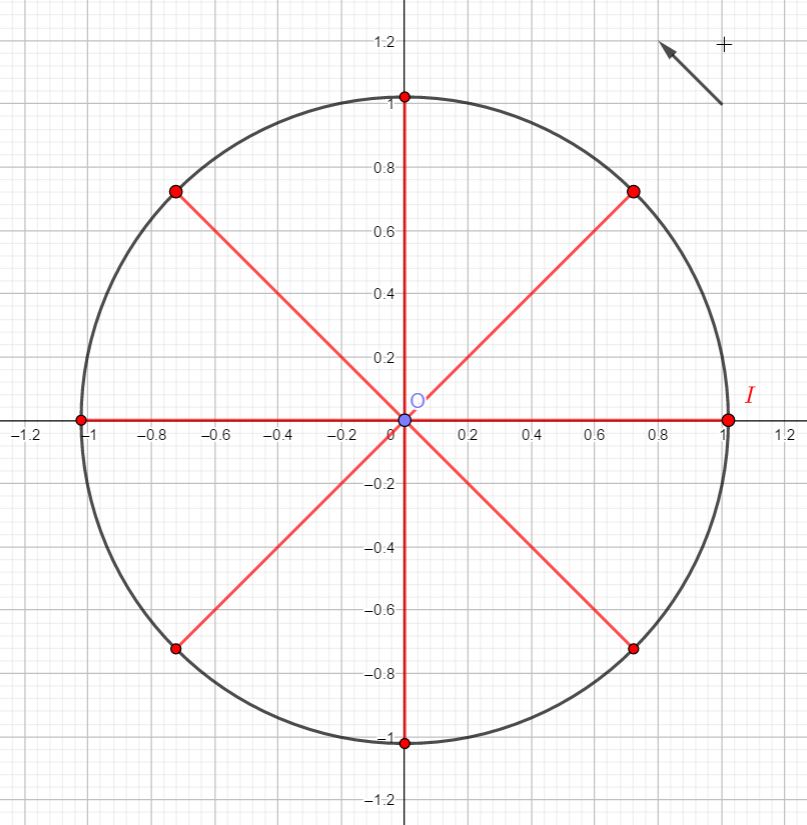
4. Comment partager un cercle en 6 parts égales ? Combien mesurent alors ces arcs de cercle ?

Le radian

Définition :

On considère le cercle trigonométrique de centre $O$ est celui qui a pour rayon $\frac{\pi}{2}$ .

La mesure en radians de l’angle au centre correspond à la mesure de l’arc orienté.

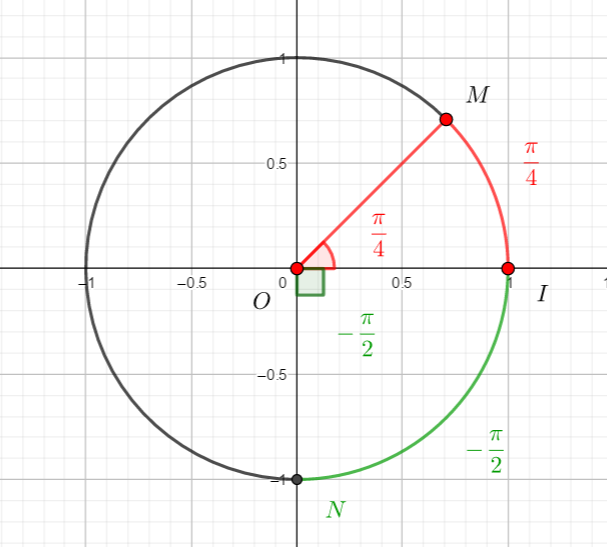
Exemples : l’arc orienté $IM$ mesure $\frac{\pi}{4}$ donc l’angle orienté $\widehat{IOM}$ mesure $\frac{\pi}{4}$ .

L’arc orienté $IN$ mesure $-\frac{\pi}{2}$ donc l’angle orienté $\widehat{ION}$ mesure $-\frac{\pi}{2}$ .

Recopier et compléter le tableau suivant :

radians	$\frac{\pi}{6}$	$\frac{\pi}{4}$		$\frac{\pi}{2}$	$\pi$
degrés			$60$		$180$	$360$

Comment placer sur le cercle trigonométrique un point associé à un nombre.

Exemple n°1

Placer sur le cercle trigonométrique le point $A(\frac{\pi}{2})$ .

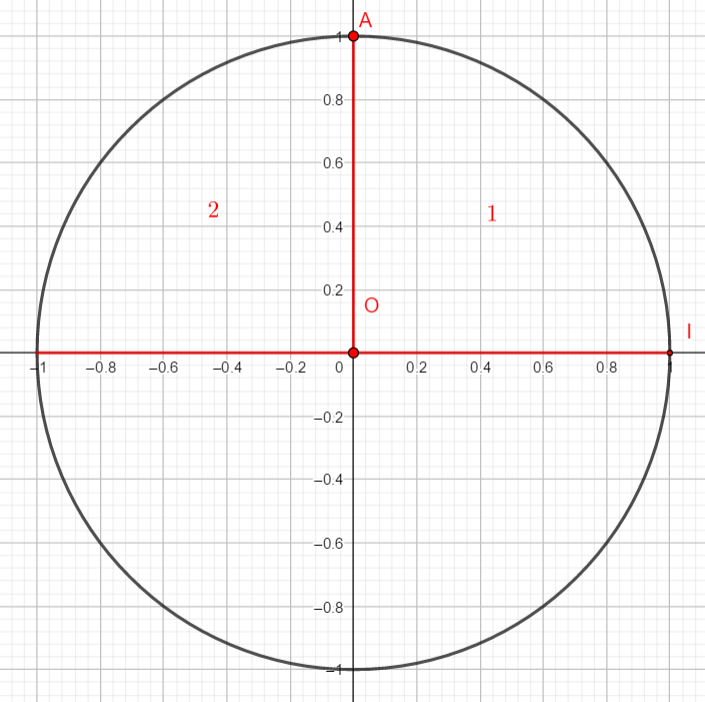
Il faut à partir du point $I$ , reporter un arc de cercle mesurant $\frac{\pi}{2}$ .

Comment procéder ?

$\frac{\pi}{2}$ correspond à une fois $\pi$ divisé par 2.

Donc on partage le ou les demi-cercle(s) en 2 et on prend 1 partie à partir du point $I$ en partant dans le sens positif ( le sens inverse des aiguilles d’une montre) .

Exemple n°2

Placer sur le cercle trigonométrique le point $A(\frac{3\pi}{4})$ .

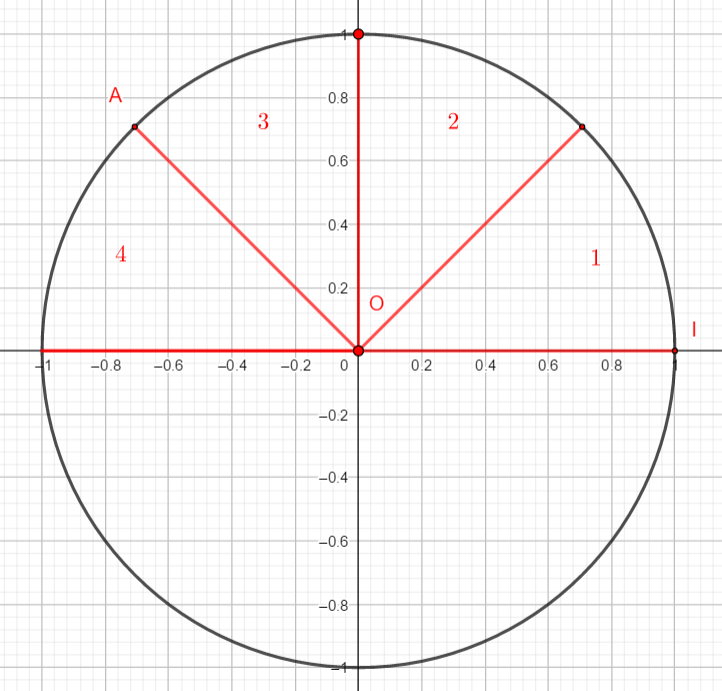
Il faut à partir du point $I$ , reporter un arc de cercle mesurant $\frac{3\pi}{4}$ .

Comment procéder ?

$\frac{3\pi}{4}$ correspond à 3 fois $\pi$ divisé par 4.

Donc on partage le ou les demi-cercle(s) en 4 et on prend 3 parties à partir du point $I$ en partant dans le sens positif ( le sens inverse des aiguilles d’une montre) .

Exemple n°3

Placer sur le cercle trigonométrique le point $A(\frac{-5\pi}{4})$ .

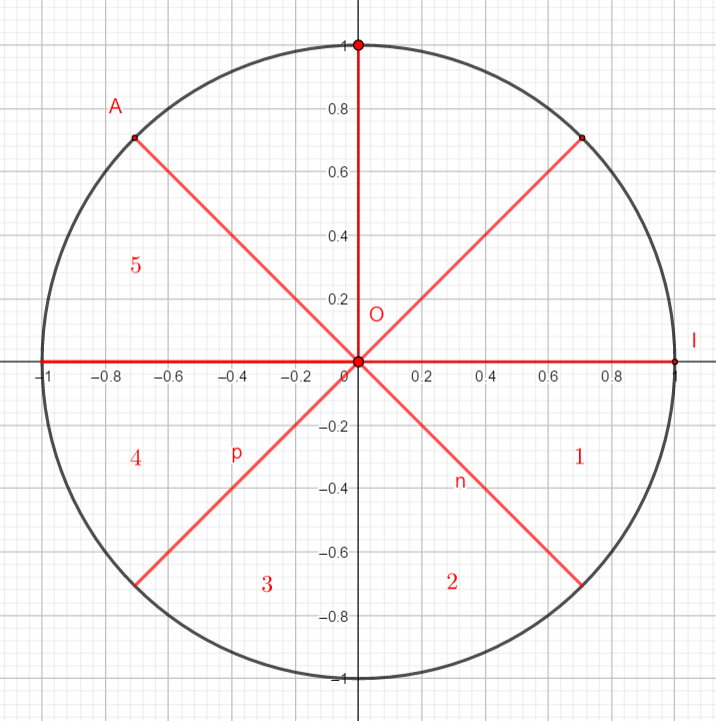
Il faut à partir du point $I$ , reporter un arc de cercle orienté mesurant $-\frac{5\pi}{4}$ .

Comment procéder ?

$\frac{5\pi}{4}$ correspond à 5 fois $\pi$ divisé par 4.

Donc on partage le ou les demi-cercle(s) en 4 et on prend 5 parties à partir du point $I$ en partant dans le sens négatif( le sens des aiguilles d’une montre) .

Exemple n°4

Placer sur le cercle trigonométrique le point $A(\frac{-4\pi}{3})$ .

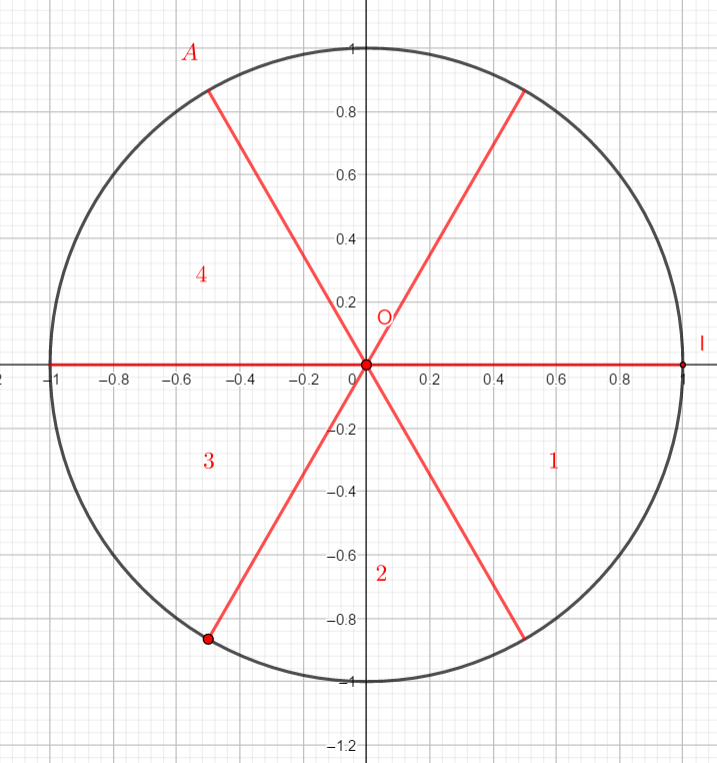
Il faut à partir du point $I$ , reporter un arc de cercle orienté mesurant $-\frac{4\pi}{3}$ .

Comment procéder ?

$\frac{4\pi}{3}$ correspond à 4 fois $\pi$ divisé par 3.

Donc on partage le ou les demi-cercle(s) en 3 et on prend 4 parties à partir du point $I$ en partant dans le sens négatif( le sens des aiguilles d’une montre) .

Exemple n°5

Placer sur le cercle trigonométrique le point $A(-\frac{8\pi}{3})$ .

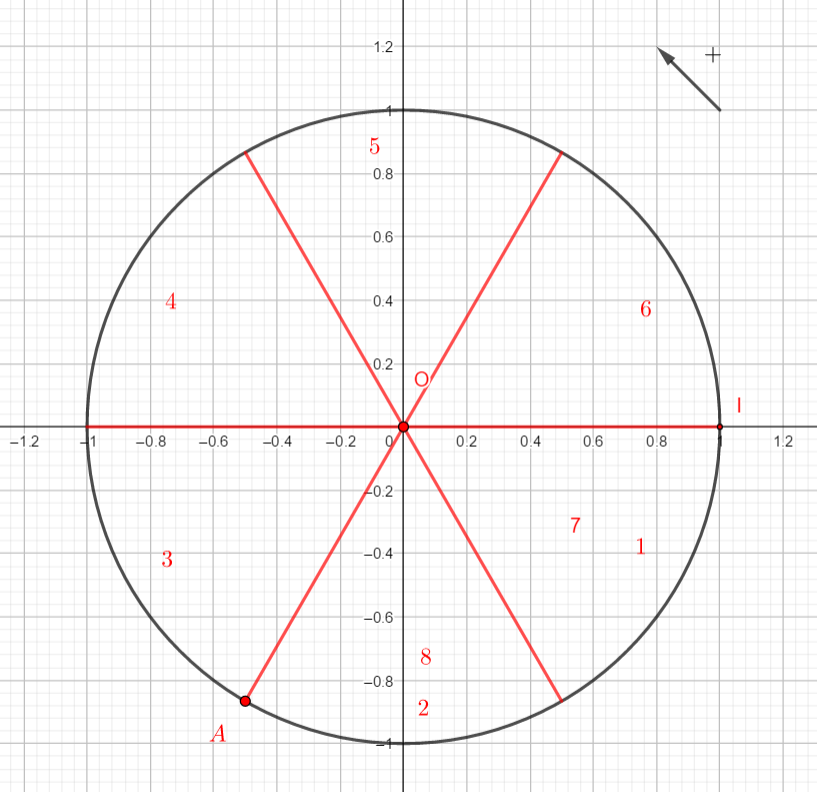
Il faut à partir du point $I$ , reporter un arc de cercle orienté mesurant $\frac{8\pi}{3}$ .

Comment procéder ?

$\frac{8\pi}{3}$ correspond à 8 fois $\pi$ divisé par 3.

Donc on partage le ou les demi-cercle(s) en 3 et on prend 8 parties à partir du point $I$ en partant dans le sens négatif ( le sens des aiguilles d’une montre) .

Comment placer sur le cercle trigonométrique un point associé à un nombre à l’aide du logiciel géogébra.

On veut placer sur le cercle trigonométrique le point $A(\frac{3\pi}{4})$ . Tout d’abord on va convertir la mesure de l’angle en degrés en utisant le tableau suivant :

radians	$\frac{\pi}{6}$	$\frac{\pi}{4}$	$\frac{\pi}{3}$	$\frac{\pi}{2}$	$\pi$	$2\pi$
degrés	$30$	$45$	$60$	$90$	$180$	$360$

Comme $\frac{\pi}{4}$ correspond à $45$ , $\frac{3\pi}{4}$ correspond à $3\times 45=135$ .

Tracer le cercle trigonométrique.

Pour cela cliquer sur le 6ème onglet en haut à partir de la gauche et sélectionner Cercle (centre-rayon).Dans le repère cliquer sur l’origine du repère, le logiciel appelle ce point A, le renommer O et saisir la valeur 1 pour le rayon.

Ne pas hésiter à agrandir la figure.

Pour cela cliquer sur le 11ème onglet en haut à partir de la gauche et sélectionner Agrandissement. Dans le repère cliquer sur l’origine du repère plusieurs fois.

Placer le point de coordonnées $I(1;0)$

Pour cela cliquer sur le 2ème onglet en haut à partir de la gauche et sélectionner Point. Dans le repère cliquer sur le point de coordonnées $(1;0)$ , le logiciel appelle ce point A, le renommer $I$ .

Placer $A(\frac{3\pi}{4})$

Pour cela cliquer sur le 8ème onglet en haut à partir de la gauche et sélectionner Angle de mesure donnée. Dans le repère cliquer sur le point $I$ et sur le point $0$ , le logiciel demande la mesure de l’angle, saisir 135°, choisir le sens positif c’est-à-dire le sens anti-horaire et faire OK. Le point souhaité appararaît sur le cercle.

Exercice n°1

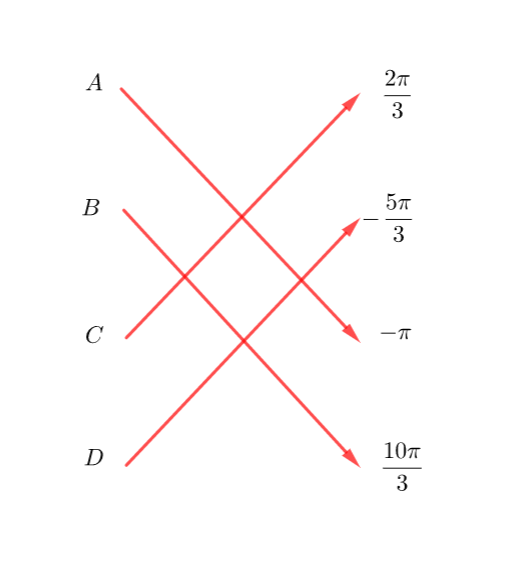
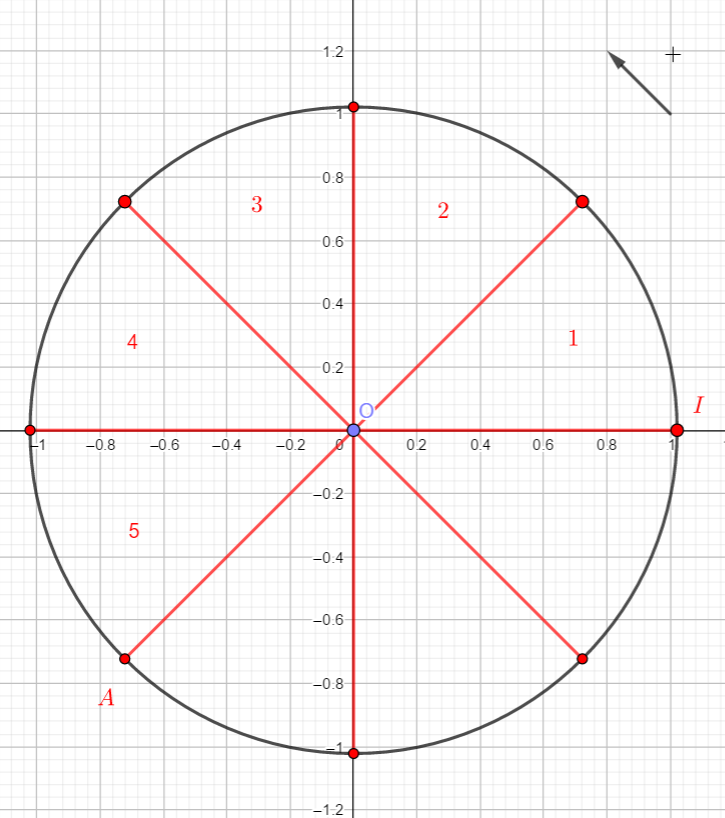
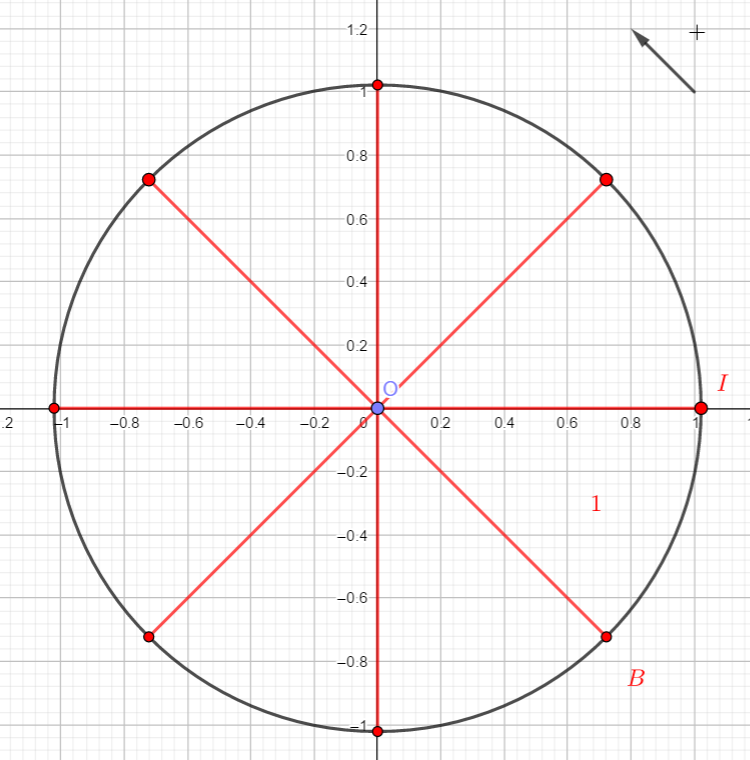
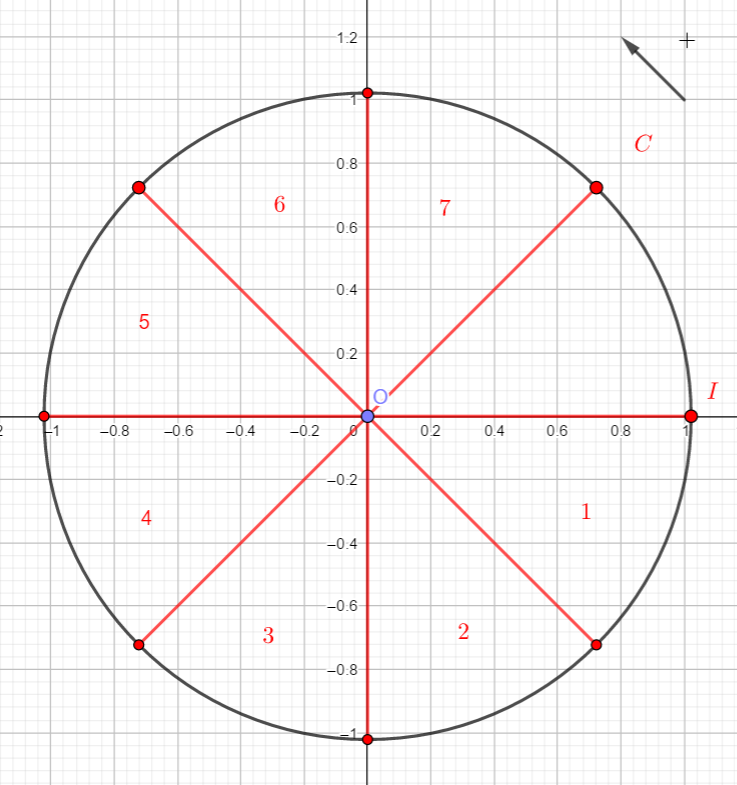
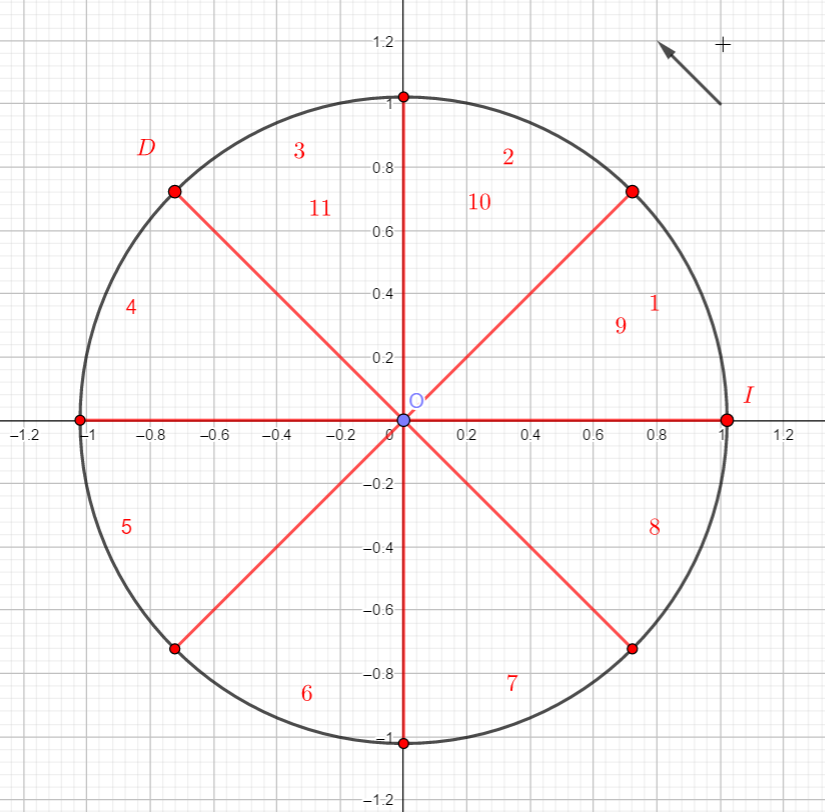
Relier par une flèche chacun des points de la figure au nombre qui lui correspond.

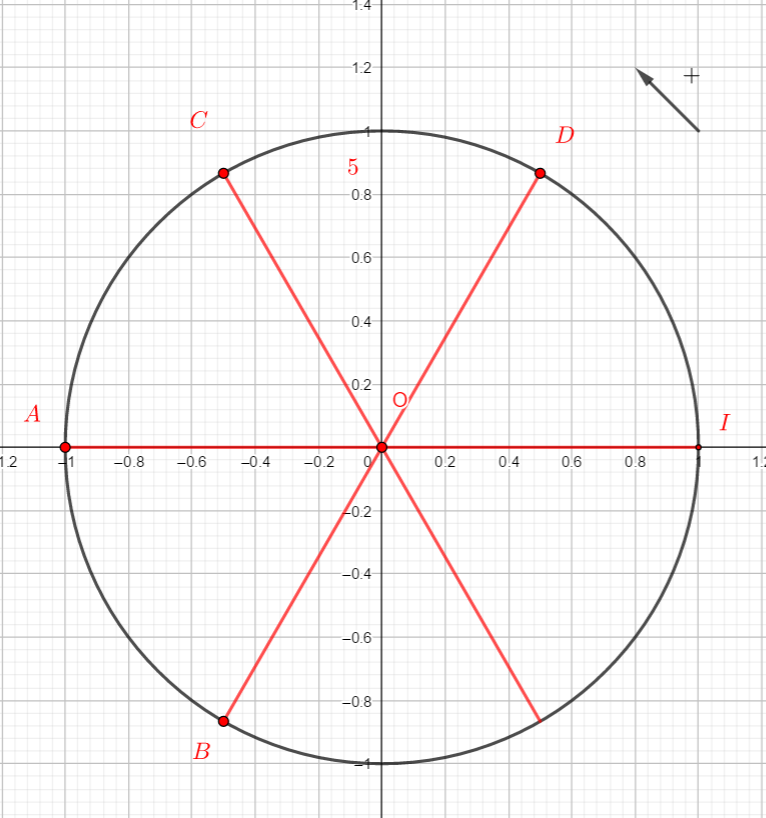
$A$ . $\hspace{4cm}.\frac{2\pi}{3}\\B$ . $\hspace{4cm}.\frac{-5\pi}{3}\\C$ . $\hspace{4cm}.-\pi\\D$ . $\hspace{4cm}.\frac{10\pi}{3}$

Exercice n°2

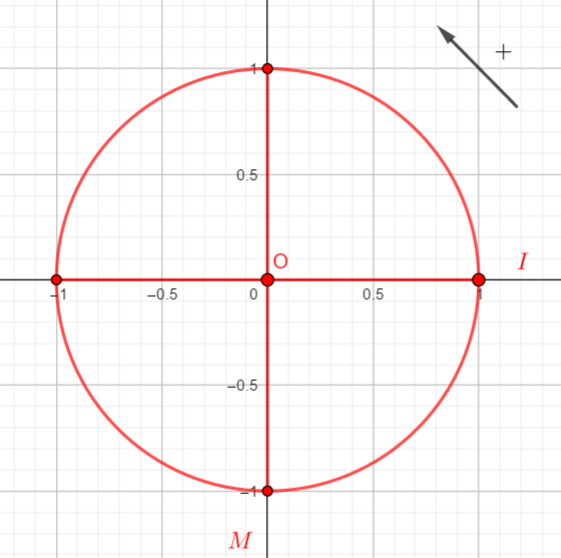
Dans chaque cas, placer le point image du nombre réel donné.

$A(\frac{5\pi}{4})$

$B(\frac{-\pi}{4})$

$C(\frac{-7\pi}{4})$

$D(\frac{11\pi}{4})$

Exercice n°3

Ecrire le nombre réel $\frac{7\pi}{2}$ sous la forme $x+2k\pi$

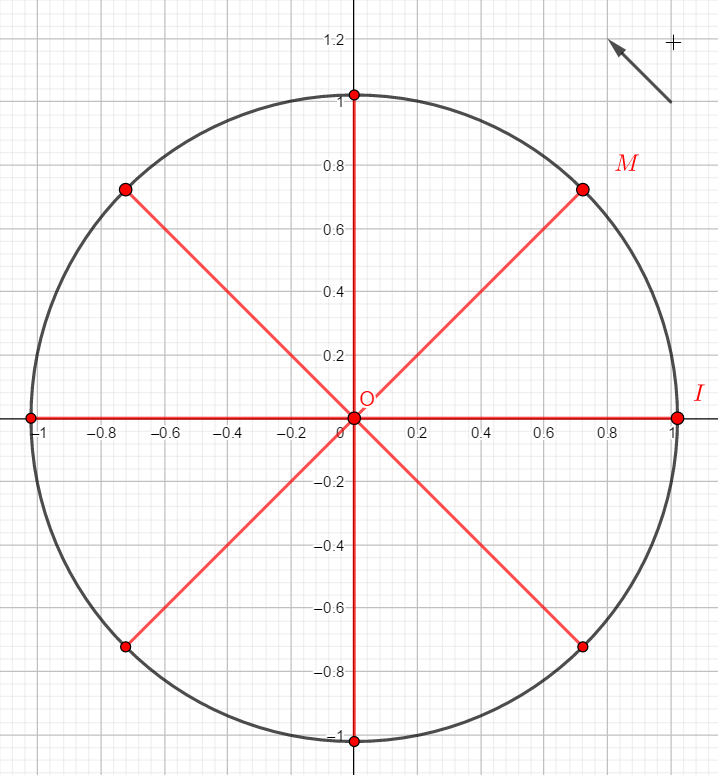
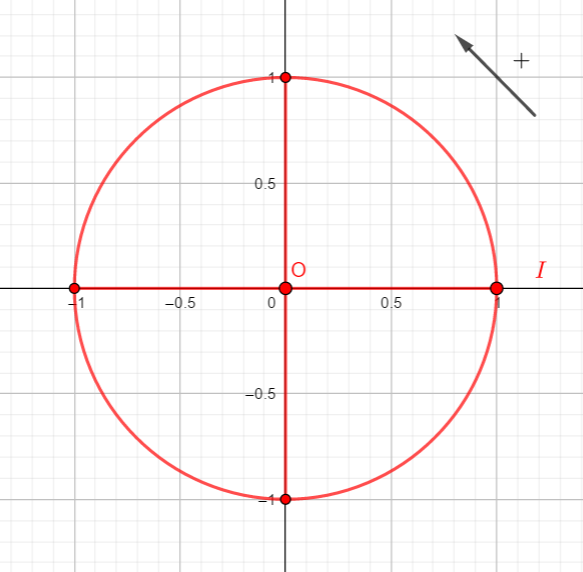
2. Reproduire la figure et placer alors sur le cercle trigonométrique $M$ , le point image du nombre réel $\frac{7\pi}{2}$ .

Exercice n°4

Ecrire le nombre réel $\frac{49\pi}{4}$ sous la forme $x+2k\pi$

2. Reproduire la figure et placer alors sur le cercle trigonométrique $M$ , le point image du nombre réel $\frac{49\pi}{4}$ .

Exercice n°5

Ecrire le nombre réel $\frac{19\pi}{3}$ sous la forme $x+2k\pi$

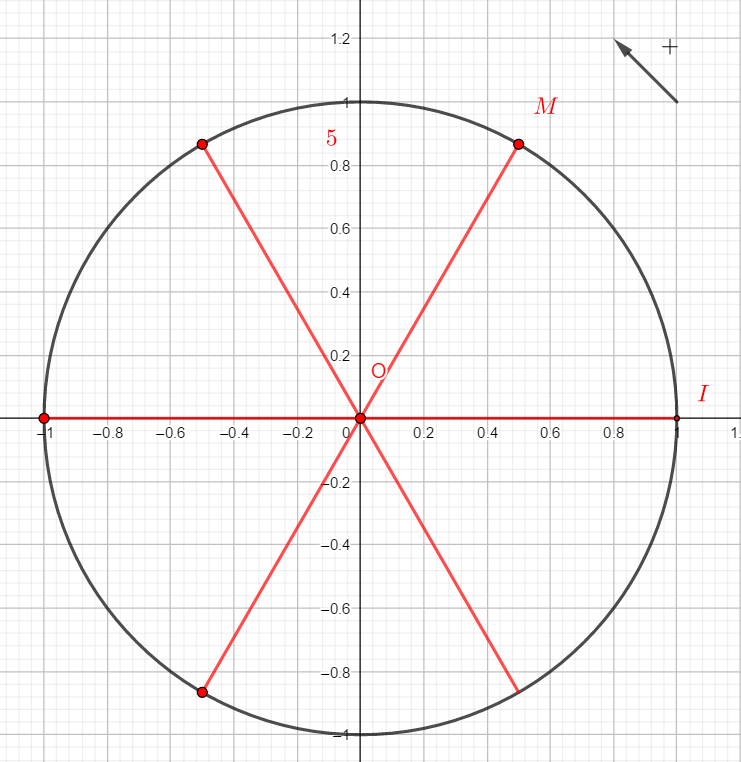
2. Reproduire la figure et placer alors sur le cercle trigonométrique $M$ , le point image du nombre réel $\frac{19\pi}{3}$ .

Prolongement possible mais hors-programme : mesure principale d’un angle.

On a vu qu’un angle possède une infinité de mesures en radians qui diffèrent toute d’un multiple de $2\pi$ . La mesure principale est celle qui se trouve dans l’intervalle $]-\pi;\pi]$ .

Exemple : parmi les mesures suivantes qui correspondent au même angle $\frac{49\pi}{2}$ ; $\frac{5\pi}{2}$ ; $-\frac{3\pi}{2}$ ; $\frac{\pi}{2}$ ; $\frac{17\pi}{2}$ , seule la mesure $\frac{\pi}{2}$ se trouve dans $]-\pi;\pi]$ . C’est la mesure principale.

Comment la déterminer ?

Prenons par exemple la mesure $\frac{172\pi}{3}$ , ce n’est pas une mesure comprise dans $]-\pi;\pi]$ , elle est trop grande. Il faut enlever $2\pi$ autant de fois que c’est possible ce qui revient à diviser par $2\pi$ .

L’objectif est de compléter les pointillés pour obtenir le quotient et le reste.

\frac{172\pi}{3}=…\times 2\pi+…

Le $3$ au dénominateur dérange, on multiplie par $3$ de chaque côté.

172\pi=…\times 6\pi+…

Le facteur $\pi$ dérange, on divise par $\pi$ de chaque côté.

172=…\times 6+…

J’effectue la division euclidienne avec quotient et reste.

172=28\times 6+4

Tout à l’heure on a divisé par $\pi$ , maintenant il faut multiplier par $\pi$ .

172\pi=28\times 6\pi+4\pi

Tout à l’heure on a multiplié par $3$ , maintenant il faut diviser par $3$ .

$\frac{172\pi}{3}=28\times \frac{6\pi}{3}+\frac{4\pi}{3}$ .

$\frac{172\pi}{3}=28\times {2\pi}+\frac{4\pi}{3}$ .

Cette égalité signifie que dans $\frac{172\pi}{3}$ , on peut enlever $28$ fois $2\pi$ et qu’il reste $\frac{4\pi}{3}$ .

$\frac{4\pi}{3}$ n’est pas la mesure principale car il ne se trouve pas dans l’intervalle $]-\pi;\pi]$ , il est trop grand.

On enlève $2\pi$ .

$\frac{4\pi}{3}-2\pi=\frac{4\pi}{3}-\frac{6\pi}{3}\\\hspace{1.3cm}=-\frac{2\pi}{3}\\-\frac{2\pi}{3}$ est la mesure principale car elle se trouve dans l’intervalle $]-\pi;\pi]$ .