Sommaire
Activité
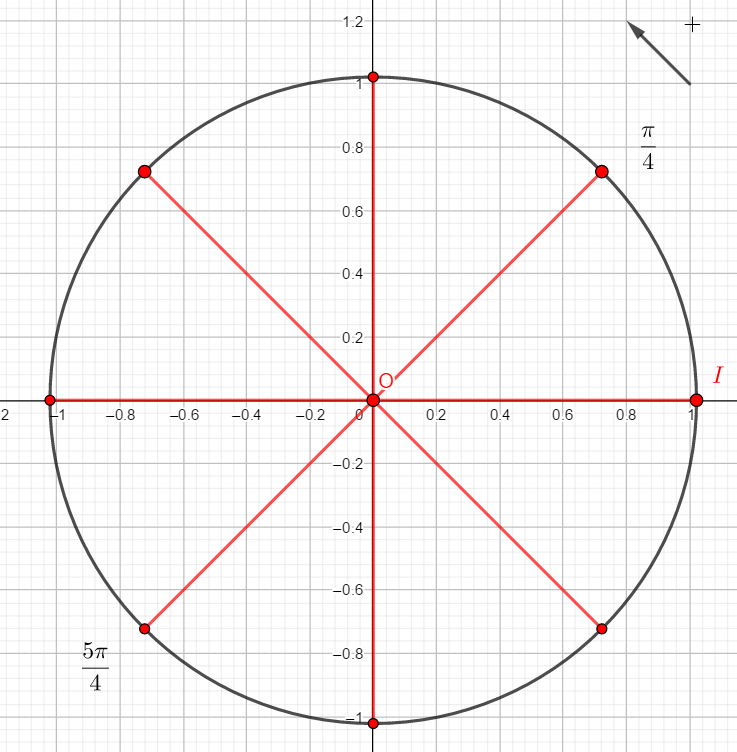
Dans la fenêtre Géogébra, placer les points I(0), A(\frac{\pi}{6}), B(\frac{\pi}{4}), C(\frac{\pi}{3}), D(\frac{\pi}{2}) et E(\frac{\pi}{6}) sur le cercle trigonométrique.
Comment placer sur le cercle trigonométrique un point associé à un nombre à l’aide du logiciel géogébra.
On veut par exemple, placer sur le cercle trigonométrique le point A(\frac{\pi}{6}). Tout d’abord on va convertir la mesure de l’angle en degrés en utilisant le tableau suivant :
radians | \frac{\pi}{6} | \frac{\pi}{4} | \frac{\pi}{3} | \frac{\pi}{2} | \pi | 2\pi |
degrés | 30 | 45 | 60 | 90 | 180 | 360 |
\frac{\pi}{6} correspond à 30°.
Tracer le cercle trigonométrique.
Pour cela cliquer sur le 6ème onglet en haut à partir de la gauche et sélectionner Cercle (centre-rayon).Dans le repère cliquer sur l’origine du repère, le logiciel appelle ce point A, le renommer O et saisir la valeur 1 pour le rayon.
Ne pas hésiter à agrandir la figure.
Pour cela cliquer sur le 11ème onglet en haut à partir de la gauche et sélectionner Agrandissement. Dans le repère cliquer sur l’origine du repère plusieurs fois.
Placer le point de coordonnées I(1;0)
Pour cela cliquer sur le 2ème onglet en haut à partir de la gauche et sélectionner Point. Dans le repère cliquer sur le point de coordonnées (1;0), le logiciel appelle ce point A, le renommer I.
Placer A(\frac{\pi}{6})
Pour cela cliquer sur le 8ème onglet en haut à partir de la gauche et sélectionner Angle de mesure donnée. Dans le repère cliquer sur le point I et sur le point 0, le logiciel demande la mesure de l’angle, saisir 30°, choisir le sens positif c’est-à-dire le sens anti-horaire et faire OK. Le point souhaité apparaît sur le cercle.
- Lire les coordonnées des points dans la colonne de gauche de la fenêtre géogébra ci-dessus. Puis reproduire et compléter le tableau ci-dessous.
| I | A | B | C | D | E | |
| Abscisse | ||||||
| Ordonnée |
2. Reproduire et compléter le tableau ci-dessous à l’aide de la calculatrice.
| \alpha | 0 | \frac{\pi}{6} | \frac{\pi}{4} | \frac{\pi}{3} | \frac{\pi}{2} | \pi |
| cos(\alpha) | ||||||
| sin(\alpha) |
3. Comparer les deux tableaux remplis.
Définitions
Soit un repère orthonormé direct (O, \overrightarrow{i},\overrightarrow{j} ) .
On considère un cercle trigonométrique de centre O.
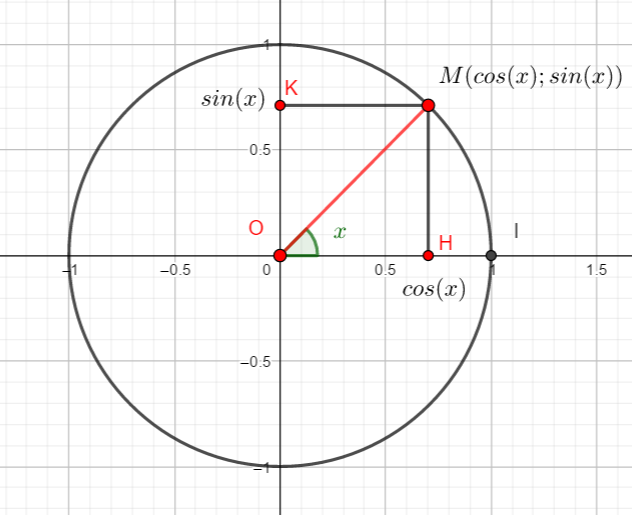
Soit M(x) un point situé sur le cercle trigonométrique.
Le cosinus de x noté cos(x) est l’abscisse du point M.
Le sinus de x noté sin(x) est l’ordonnée du point M.
Exemple :
Le nombre réel \frac{3\pi}{2} a pour image le point de coordonnées (0;-1) donc cos(\frac{3\pi}{2})=0 et sin(\frac{3\pi}{2})=-1.
Propriétés :
Pour tout nombre réel x
-1\leq cos(x)\leq 1
-1\leq sin(x)\leq 1
cos^2(x)+sin^2(x)=1
Démonstration :
- cos(x) est l’abscisse d’un point du cercle trigonométrique donc -1\leq cos(x)\leq 1.
- sin(x) est l’ordonnée d’un point du cercle trigonométrique donc -1\leq sin(x)\leq 1.
- Dans le triangle rectangle OHM, on applique le théorème de Pythagore.
On remplace OH par cos(x), HM par sin(x) et OM par 1 car le rayon du cercle trigonométrique est 1.
cos^2(x)+sin^2(x)=1 .
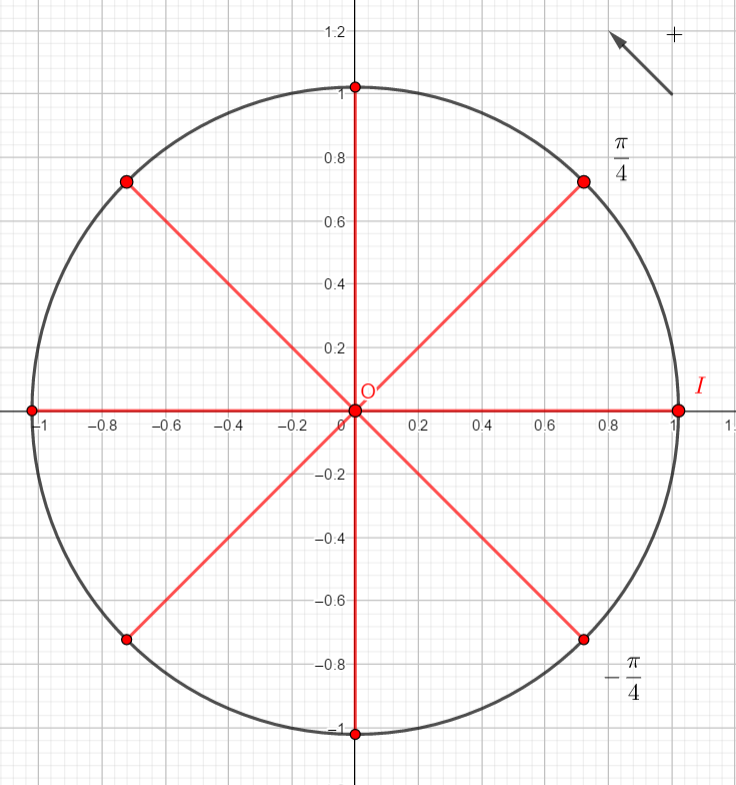
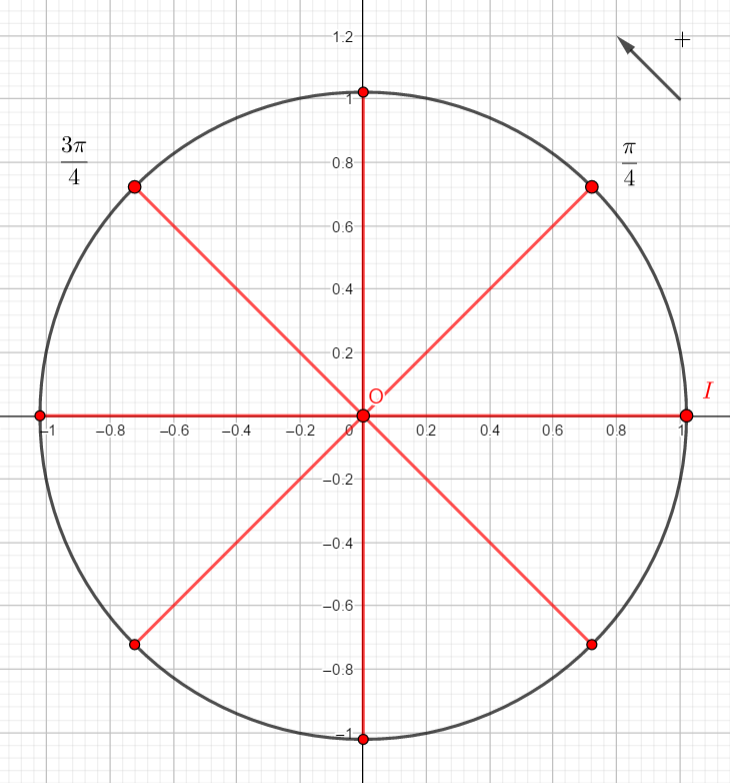
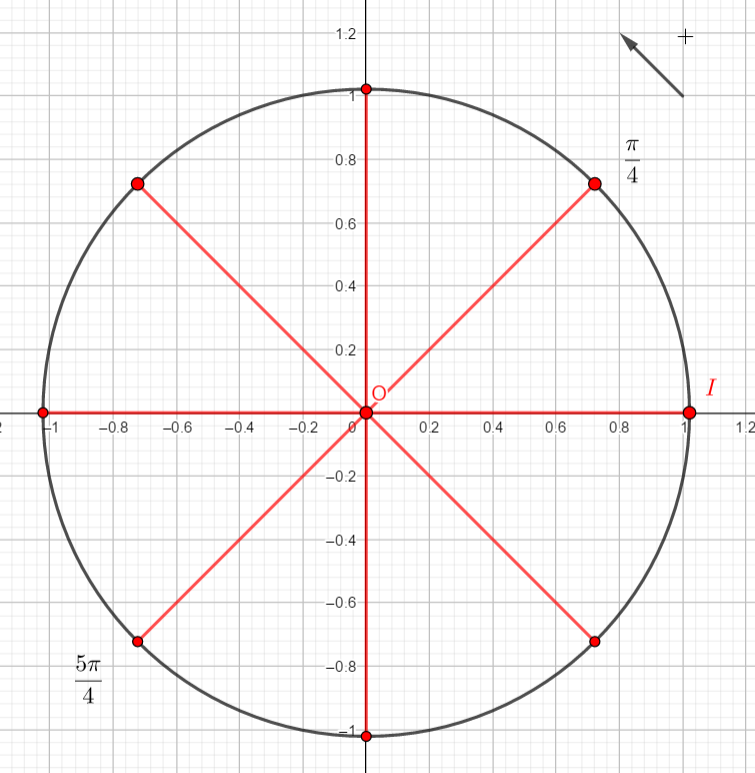
Exercice n°1
On rappelle que cos(\frac{\pi}{4})=\frac{\sqrt{2}}{2} et que sin(\frac{\pi}{4})=\frac{\sqrt{2}}{2}.
Reproduire la figure et placer sur le cercle le point image de \frac{\pi}{4}. Puis par lecture sur le cercle trigonométrique et en utilisant des symétries, déterminer les cosinus et sinus demandés.
- cos(-\frac{\pi}{4}) et sin(-\frac{\pi}{4})
2. cos(\frac{3\pi}{4}) et sin(\frac{3\pi}{4})
3. cos(\frac{5\pi}{4}) et sin(\frac{5\pi}{4})
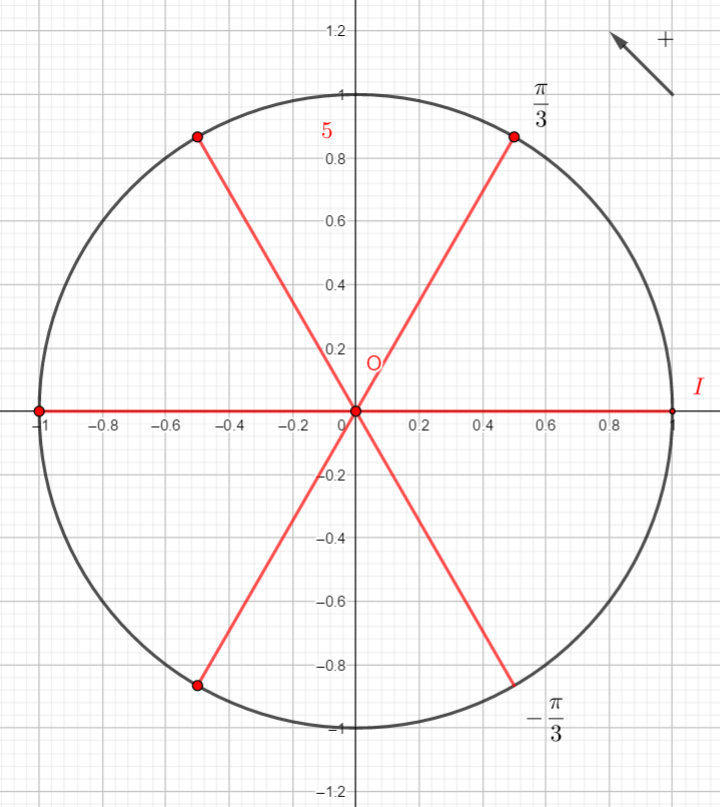
Exercice n°2
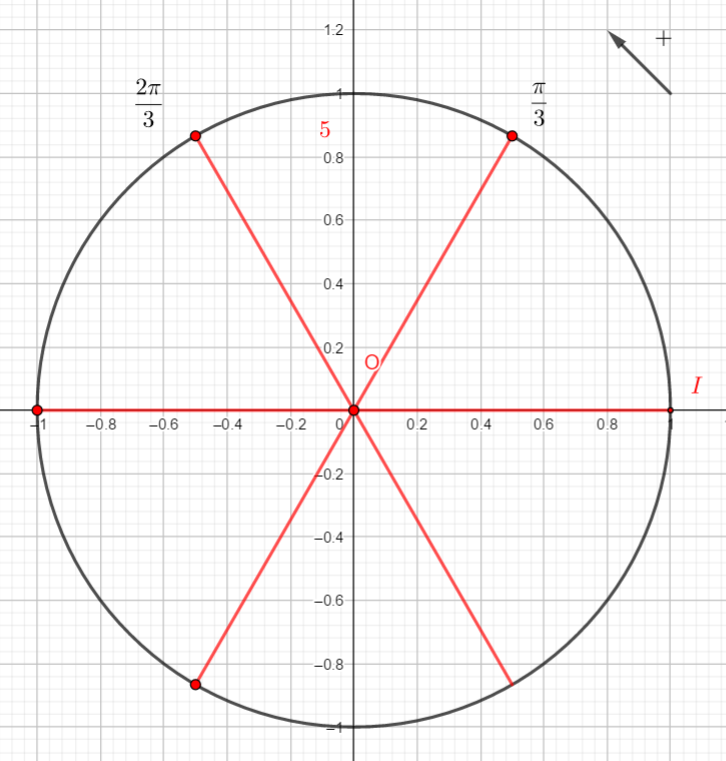
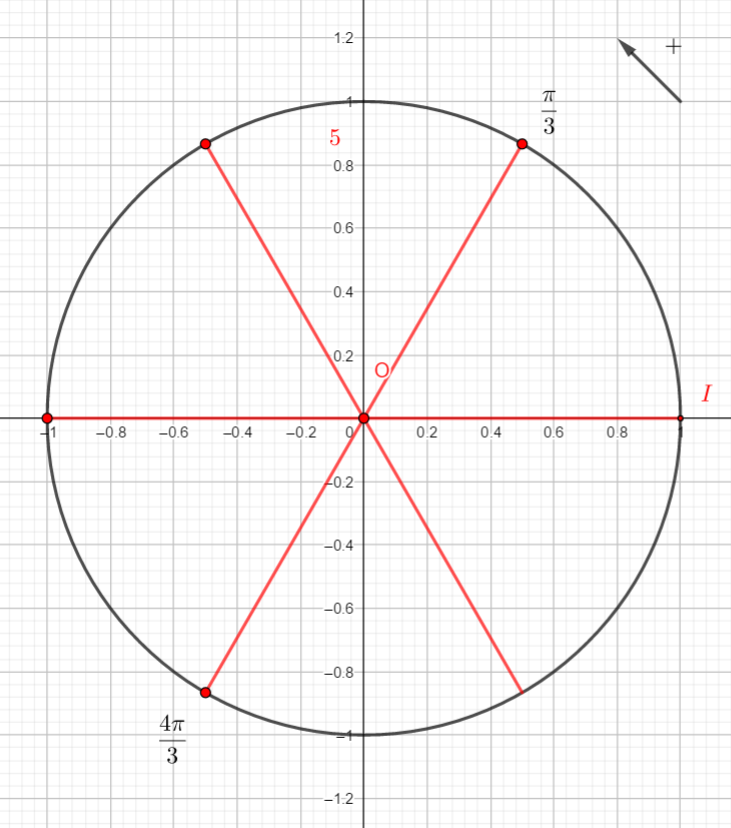
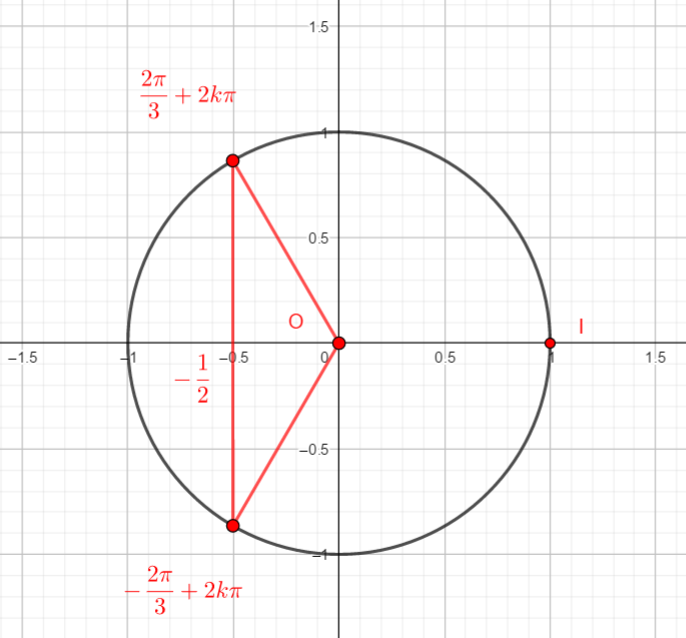
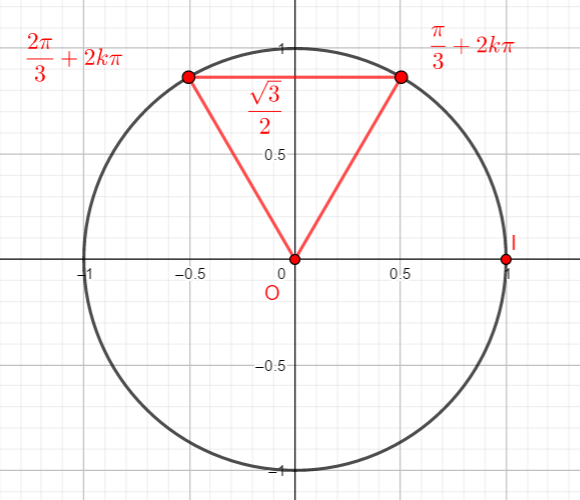
On rappelle que cos(\frac{\pi}{3})=\frac{1}{2} et que sin(\frac{\pi}{3})=\frac{\sqrt{3}}{2}.
Reproduire la figure et placer sur le cercle le point image de \frac{\pi}{3}. Puis par lecture sur le cercle trigonométrique et en utilisant des symétries, déterminer les cosinus et sinus demandés.
- cos(-\frac{\pi}{3}) et sin(-\frac{\pi}{3})
2. cos(\frac{2\pi}{3}) et sin(\frac{2\pi}{3})
3. cos(\frac{4\pi}{3}) et sin(\frac{4\pi}{3})
Exercice n°3
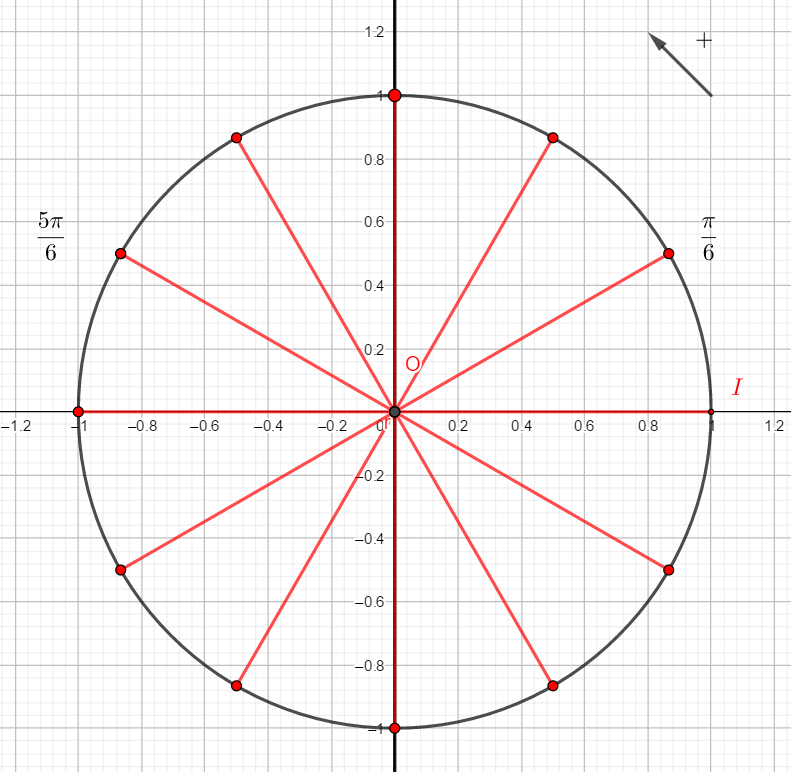
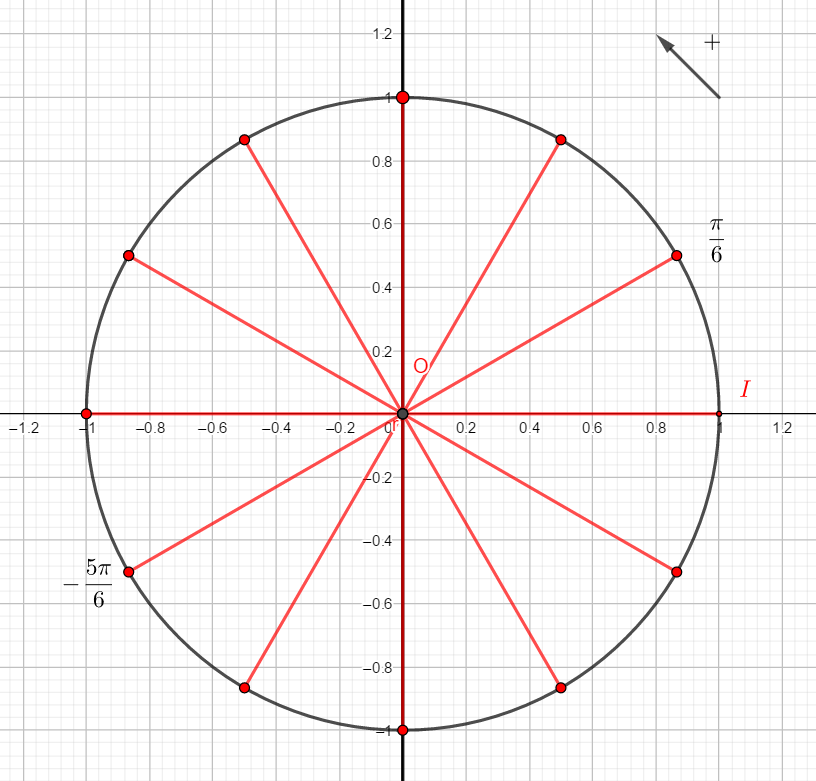
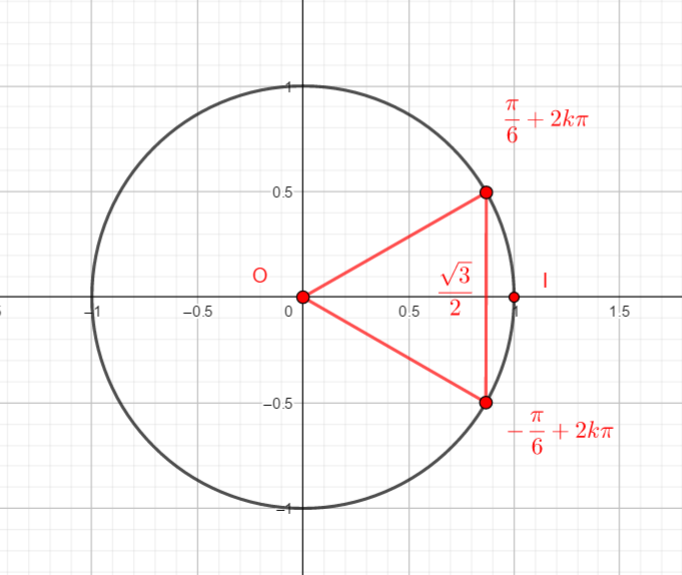
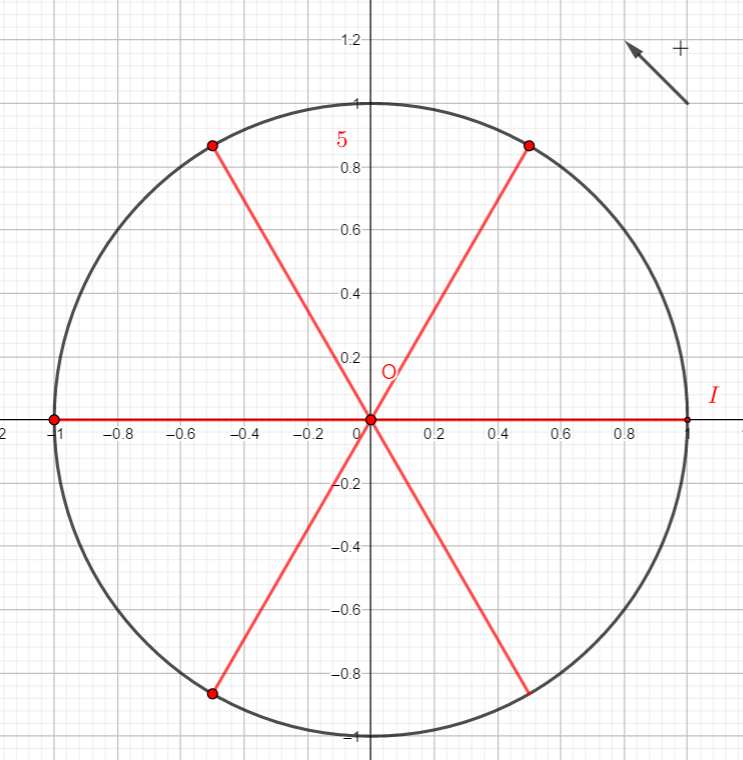
On rappelle que cos(\frac{\pi}{6})=\frac{\sqrt{3}}{2} et que sin(\frac{\pi}{3})=\frac{1}{2}.
Reproduire la figure et placer sur le cercle le point image de \frac{\pi}{6}. Puis par lecture sur le cercle trigonométrique et en utilisant des symétries, déterminer les cosinus et sinus demandés.
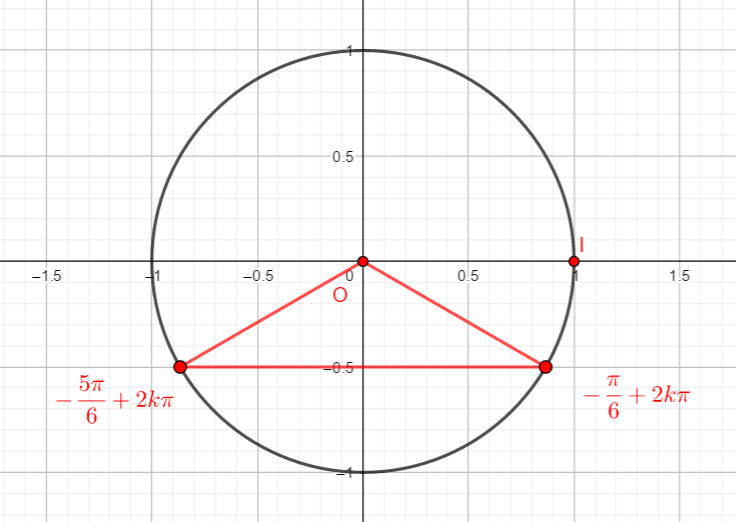
- cos(-\frac{\pi}{6}) et sin(-\frac{\pi}{6})
2. cos(\frac{5\pi}{6}) et sin(\frac{5\pi}{6})
3. cos(\frac{-5\pi}{6}) et sin(\frac{-5\pi}{6})
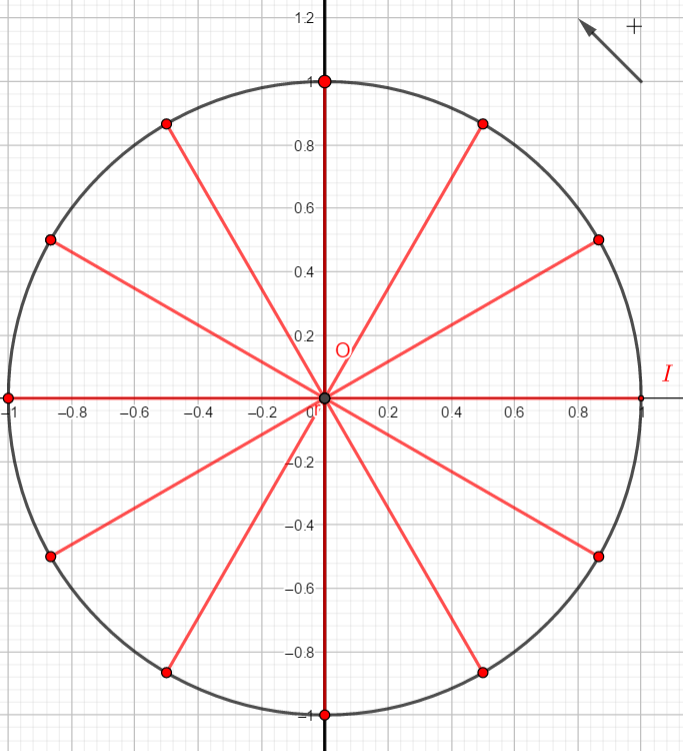
Exercice n°4
Utiliser le tableau suivant pour déterminer les cosinus et sinus de l’angle proposé. Le cas échéant, utiliser en plus un cercle trigonométrique.

1. cos(\frac{121\pi}{6}) et sin(\frac{121\pi}{6})
2. cos(\frac{37\pi}{4}) et sin(\frac{37\pi}{4})
3. cos(-\frac{25\pi}{2}) et sin(-\frac{25\pi}{2}).
Résoudre une équation du type cos(x)=k
Exemple :
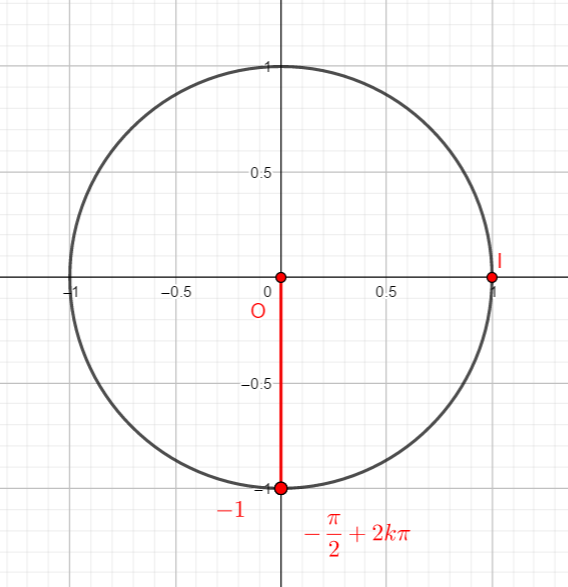
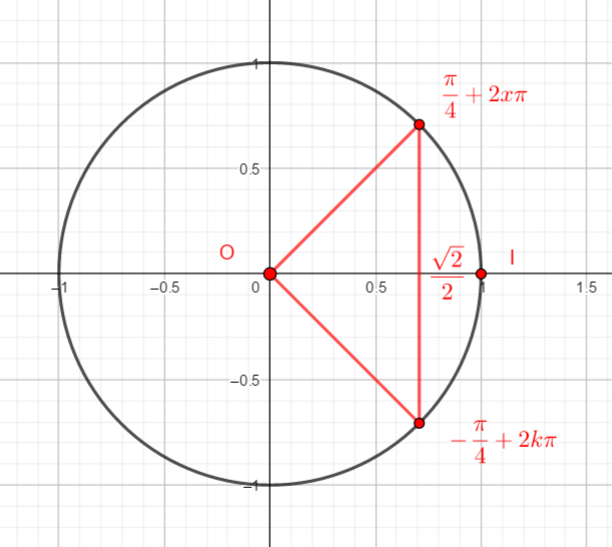
Résoudre l’équation cos(x)=\frac{\sqrt{2}}{2} sur l’intervalle [0;2\pi]
1.Avec le cercle trigonométrique
Remarque : Le point A de la fenêtre ci-dessous a été défini en tapant A=(\frac{\sqrt{2}}{2},0) dans la colonne de gauche. Pour les exercices à venir, il suffit de remplacer l’abscisse de A : \frac{\sqrt{2}}{2} par le nombre proposé dans l’énoncé.
Les deux mesures d’angles trouvées sont 45° et 315° , ce qui correspond à \frac{\pi}{4} et \frac{7\pi}{4}.
2. Avec l’application calcul Formel de Géogébra.
On a vu dans les leçons précédentes qu’un angle possède une infinité de mesures qui différent d’un multiple de 2\pi.
Pour k=0 : on obtient les solutions -\frac{\pi}{4} et \frac{\pi}{4}. Pour k=1 on obtient les solutions \frac{7\pi}{4} et \frac{9\pi}{4}.
Parmi toutes les solutions proposées, seules \frac{\pi}{4} et \frac{7\pi}{4} sont dans [0;2\pi] .
3. Ce qu’on peut écrire sur la copie
On veut résoudre l’équation cos(x)=\frac{\sqrt{2}}{2} sur l’intervalle [0;2\pi]
On identifie l’angle adéquat dans le tableau suivant ( ceci n’apparaît pas sur la copie, le tableau non plus).

On peut ensuite construire un cercle trigonométrique et représenter la situation ainsi avec l’angle adéquat précédent :
Parmi toutes les solutions proposées, seules \frac{\pi}{4} et \frac{7\pi}{4} sont dans [0;2\pi] .
4. Utiliser la TI 83 Premium.
On peut se mettre en mode degré ou mode radian, je choisis de rester en mode degré.
On tape sur la touche trig, on sélectionne 5 : cos^{-1} puis on tape \frac{\sqrt{2}}{2} et on fait entrer. Voici ce qui apparaît :
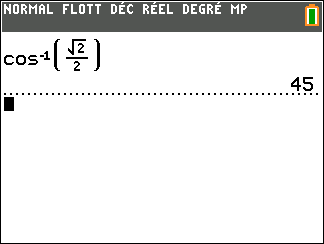
On obtient une seule solution, il faut s’assurer qu’elle est dans l’intervalle proposé ou non puis de déterminer les autres solutions. La TI 83 est moins performante que Géogébra sur ce coup-là.
Exercice n°5
Dans chaque cas, résoudre l’équation dans l’intervalle proposé. Pour conjecturer le résultat vous pouvez utiliser les deux pages Géogébra précédentes comme dans l’exemple.
- cos(x)=0 sur [-\pi;\pi]
2. cos(x)=-\frac{1}{2} sur [-\pi;\pi]
3. cos(x)=\frac{\sqrt{3}}{2} sur [0;2\pi]
4. cos(x)=1 sur [0;2\pi]
Résoudre une équation du type sin(x)=k
Exemple :
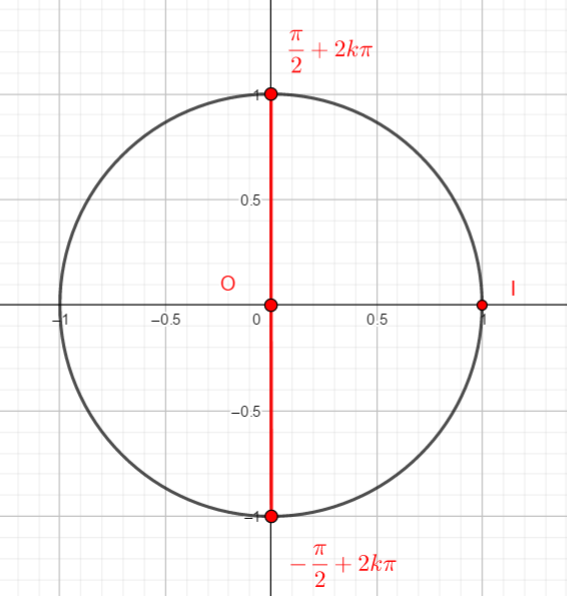
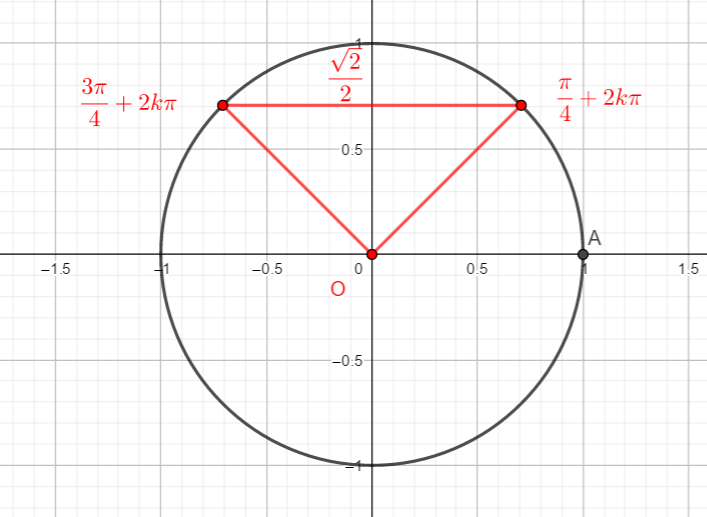
Résoudre l’équation sin(x)=\frac{\sqrt{2}}{2} sur l’intervalle [0;2\pi]
1.Avec le cercle trigonométrique
Remarque : Le point A de la fenêtre ci-dessous a été défini en tapant A=(0,\frac{\sqrt{2}}{2}) dans la colonne de gauche. Pour les exercices à venir, il suffit de remplacer l’ordonnée de A : \frac{\sqrt{2}}{2} par le nombre proposé dans l’énoncé.
Les deux mesures d’angles trouvées sont 45° et 135° , ce qui correspond à \frac{\pi}{4} et \frac{3\pi}{4}.
2. Avec l’application calcul Formel de Géogébra.
On a vu dans les leçons précédentes qu’un angle possède une infinité de mesures qui différent d’un multiple de 2\pi.
Pour k=0 : on obtient les solutions \frac{\pi}{4} et \frac{3\pi}{4}. Pour k=1 on obtient les solutions \frac{9\pi}{4} et \frac{11\pi}{4}.
Parmi toutes les solutions proposées, seules \frac{\pi}{4} et \frac{3\pi}{4} sont dans [0;2\pi] .
3. Ce qu’on peut écrire sur la copie
On veut résoudre l’équation sin(x)=\frac{\sqrt{2}}{2} sur l’intervalle [0;2\pi]
On identifie l’angle adéquat dans le tableau suivant ( ceci n’apparaît pas sur la copie, le tableau non plus).

On peut ensuite construire un cercle trigonométrique et représenter la situation ainsi avec l’angle adéquat précédent :
Parmi toutes les solutions proposées, seules \frac{\pi}{4} et \frac{3\pi}{4} sont dans [0;2\pi] .
4. Utiliser la TI 83 Premium.
On peut se mettre en mode degré ou mode radian, je choisis de rester en mode degré.
On tape sur la touche trig, on sélectionne 4 : sin^{-1} puis on tape \frac{\sqrt{2}}{2} et on fait entrer. Voici ce qui apparaît :
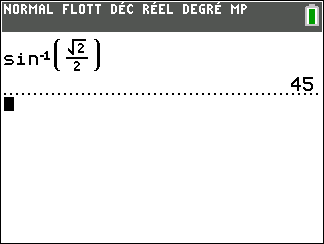
On obtient une seule solution, il faut s’assurer qu’elle est dans l’intervalle proposé ou non puis de déterminer les autres solutions. La TI 83 est moins performante que Géogébra sur ce coup-là.
Exercice n°6
Dans chaque cas, résoudre l’équation dans l’intervalle proposé. Pour conjecturer le résultat vous pouvez utiliser les deux pages Géogébra précédentes comme dans l’exemple.
- sin(x)=0 sur [-\pi;\pi]
2. sin(x)=-\frac{1}{2} sur [-\pi;\pi]
3. sin(x)=\frac{\sqrt{3}}{2} sur [0;2\pi]
4. sin(x)=-1 sur [0;2\pi]