Définitions
Définition n°1
La fonction sinus est la fonction qui, à tout nombre x réel, associe sin(x).
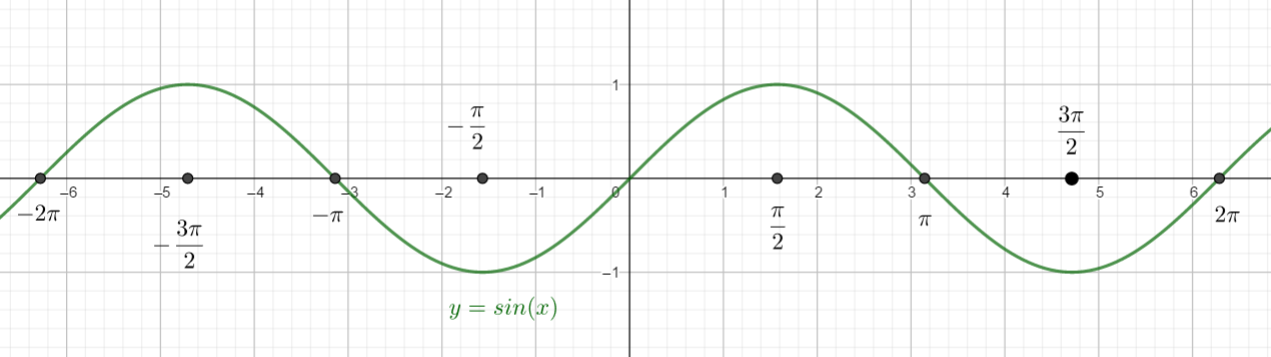
Exercice n°1
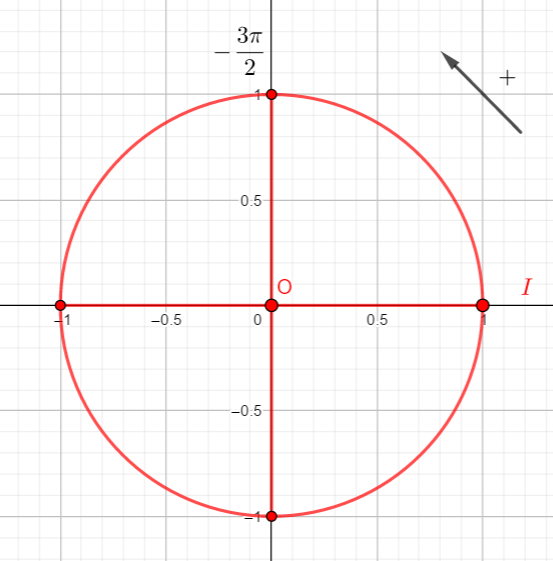
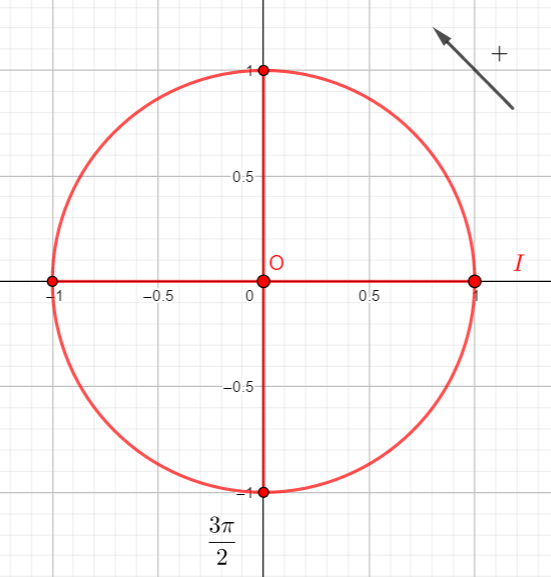
A l’aide de la courbe ci-dessus, déterminer graphiquement sin(-2\pi), sin(-\frac{3\pi}{2}), sin(0) et sin(\frac{3\pi}{2}).
Puis utiliser le cercle trigonométrique ci-contre pour confirmer vos résultats.
Définition n°2
La fonction cosinus est la fonction qui, à tout nombre x réel, associe cos(x).
Exercice n°2
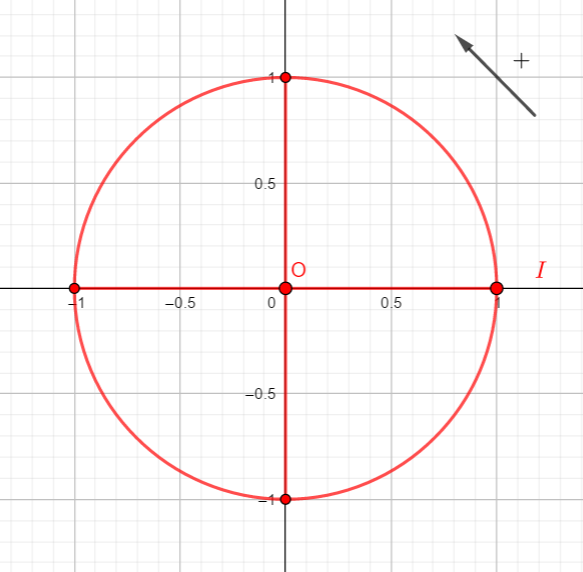
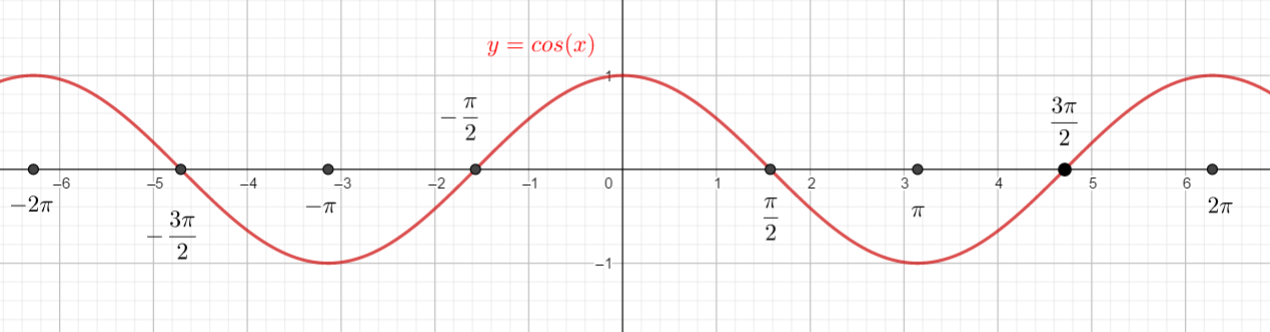
A l’aide de la courbe ci-dessus, déterminer graphiquement cos(-2\pi), cos(-\frac{3\pi}{2}), cos(0) et cos(\frac{3\pi}{2}).
Puis utiliser le cercle trigonométrique ci-contre pour confirmer vos résultats.

Parité et périodicité
Propriété n°1
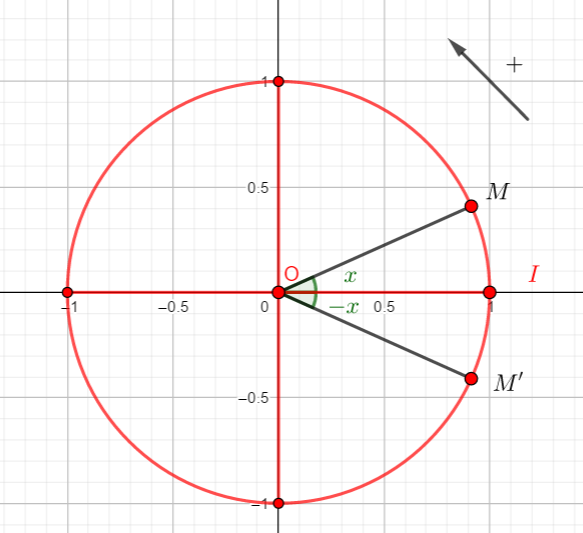
On voit bien sur le cercle que les points M et M’ respectivement associés aux réels x et -x ont des ordonnées opposées, donc :
sin(-x)=-sin(x).
On dit que la fonction sinus est impaire.
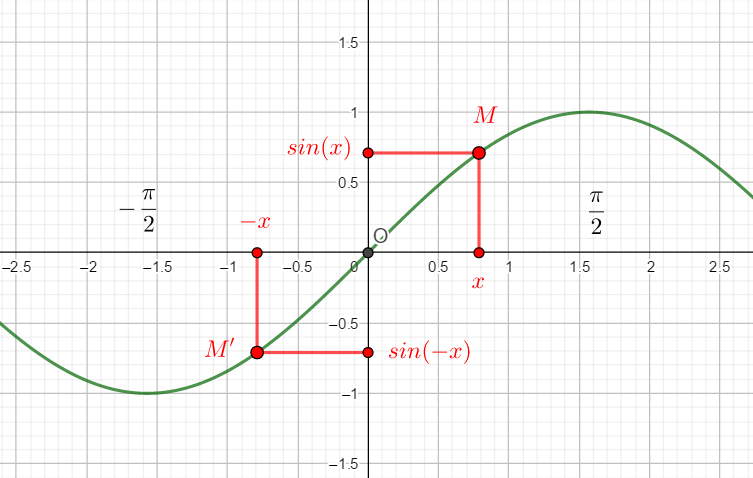
La fonction sinus est impaire, cela se traduit graphiquement par : l’origine du repère est centre de symétrie de la courbe représentative de la fonction sinus.
En effet quel que soit le point M sur la courbe, O sera toujours le milieu de [MM’].
Propriété n°2

On voit bien sur le cercle que les points M et M’ respectivement associés aux réels x et -x ont mêmes abscisses, donc :
cos(-x)=cos(x).
On dit que la fonction cosinus est paire.
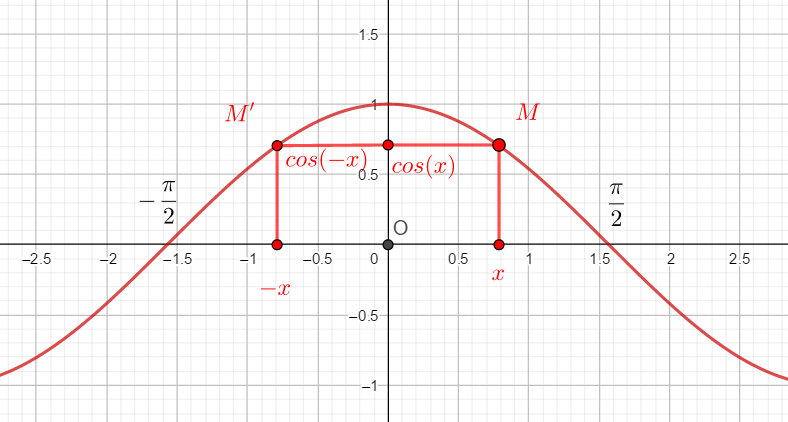
La fonction cosinus est paire, cela se traduit graphiquement par : l’axe des ordonnées est axe de symétrie de la courbe représentative de la fonction cosinus.
En effet quel que soit le point M sur la courbe, l’axe des ordonnées sera toujours la médiatrice de [MM’].
Exercice n°3
Etudier la parité des fonctions suivantes sur \mathbf{R}
- f(x)=2sin(x)cos(x)
2. f(x)=cos^2(x)-sin^2(x)
3. f(x)=sin(x)(2cos(x)+3)
4. f(x)=sin(x)+cos(x)
Propriété n°3
La fonction sinus est périodique de période 2\pi pour tout réel x, sin(x+2\pi) = sin(x)
Conséquence graphique
Il suffit de tracer une partie de la courbe de la fonction sinus sur un intervalle de longueur 2\pi par exemple [0;2\pi] (comme c’est le cas ci-dessous) en rouge. Puis comme pour une frise, on reporte ce motif à l’infini pour obtenir la courbe sur \mathbf{R} tout en entier.
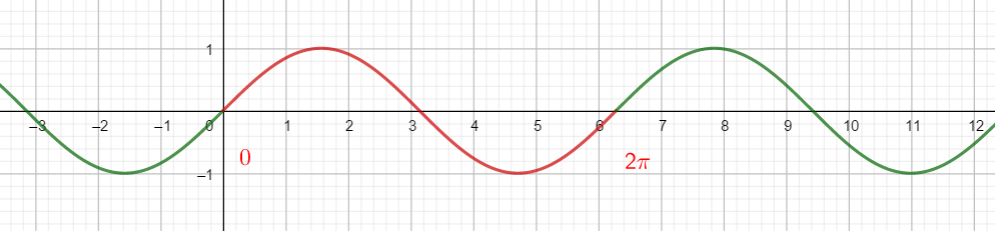
Propriété n°4
La fonction cosinus est périodique de période 2\pi pour tout réel x, cos(x+2\pi) = cos(x)
Conséquence graphique
Il suffit de tracer une partie de la courbe de la fonction cosinus sur un intervalle de longueur 2\pi par exemple [0;2\pi] (comme c’est le cas ci-dessous) en rouge. Puis comme pour une frise, on reporte ce motif à l’infini pour obtenir la courbe sur \mathbf{R} tout en entier.
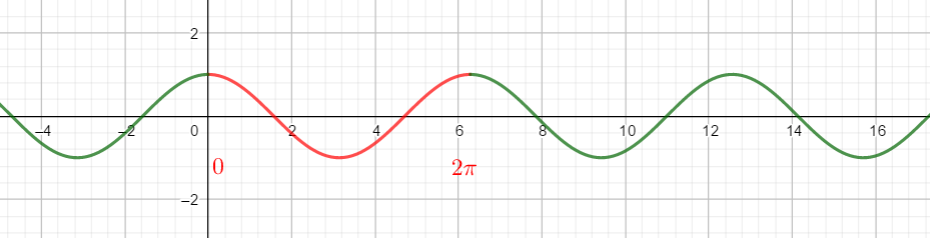
Conséquence graphique.
Exercice n°4
Dans chaque cas, montrer que la fonction f est de période T.
- f(x)=2sin(x)cos(x) , T=2\pi
2. f(x)=cos(2x) , T=\pi
3. f(x)=sin(3x) , T=\frac{2\pi}{3}
4. f(x)=sin(\frac{2\pi}{5}x) , T=5
Prolongement : variations des fonctions trigonométriques.
On va s’intéresser aux variations de la fonction cosinus sur l’intervalle [0;2\pi].
Déplacer le point M de la courbe de la gauche vers la droite. Observer comment varie l’ordonnée de ce point en regardant les coordonnées du point M dans la colonne de gauche.
Par lecture graphique, dresser le tableau de variations de la fonction cosinus sur l’intervalle [0;2\pi].
On va s’intéresser aux variations de la fonction sinus sur l’intervalle [0;2\pi].
Déplacer le point M de la courbe de la gauche vers la droite. Observer comment varie l’ordonnée de ce point en regardant les coordonnées du point M dans la colonne de gauche.
Par lecture graphique, dresser le tableau de variations de la fonction sinus sur l’intervalle [0;2\pi].