logo

1. Produit scalaire et Formule d’Al-Kashi.

Sommaire

Jamshid al-Kashi est un mathématicien et astronome perse né vers 1380 en Iran et mort en 1429.

Propriétés : formules d’Al-Kashi

Dans le triangle ABC ci-dessous

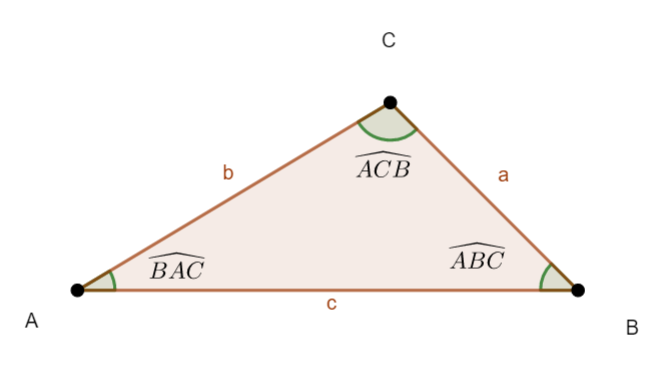
On a les égalités suivantes :

a^2=b^2+c^2-2\times b\times c\times cos(\widehat{BAC})

b^2=a^2+c^2-2\times a\times c\times cos(\widehat{ABC})

c^2=a^2+b^2-2\times a\times b\times cos(\widehat{ACB})

Démonstration de la 1ère égalité

C’est-à-dire : a^2=b^2+c^2-2\times b\times c\times cos(\widehat{BAC})\\ a^2=BC^2\\ \hspace{0.45cm}=\overrightarrow{BC}^2\\ \hspace{0.45cm}=(\overrightarrow{BA}+\overrightarrow{AC})^2\\ \hspace{0.45cm}=(\overrightarrow{AC}-\overrightarrow{AB})^2\\ \hspace{0.45cm}=\overrightarrow{AC}^2-2\overrightarrow{AC}.\overrightarrow{AB}+\overrightarrow{AB}^2\\ \hspace{0.45cm}=AC^2-2AC\times AB\times cos(\widehat{BAC})+AB^2\\ \hspace{0.45cm}=b^2+c^2-2\times b\times c\times cos(\widehat{BAC})

Application n°1 : Calculer une mesure d’angle si on connaît les longueurs des trois côtés

Exercice n°1 

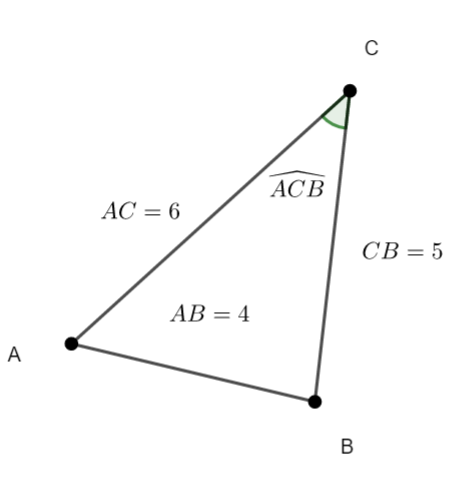
Dans le triangle ABC ci-dessous, AB=4 , AC=6 et CB=5.

Déterminer une mesure en degrés de l’angle \widehat{ACB}. Arrondir à l’unité.

correction

Application n°2 : Calculer la longueur du troisième côté si on connaît les longueurs de deux côtés et de leur angle commun.

Exercice n°2 

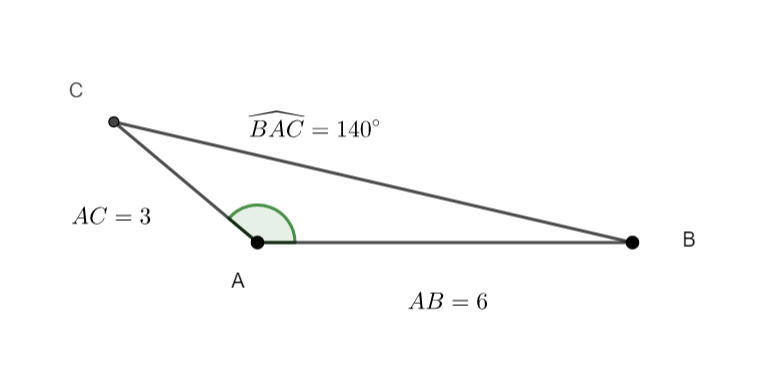
Dans le triangle ABC ci-dessous, AB=6 , AC=3 et \widehat{BAC}=140°.

Calculer la longueur BC.

correction

Exercice n°3

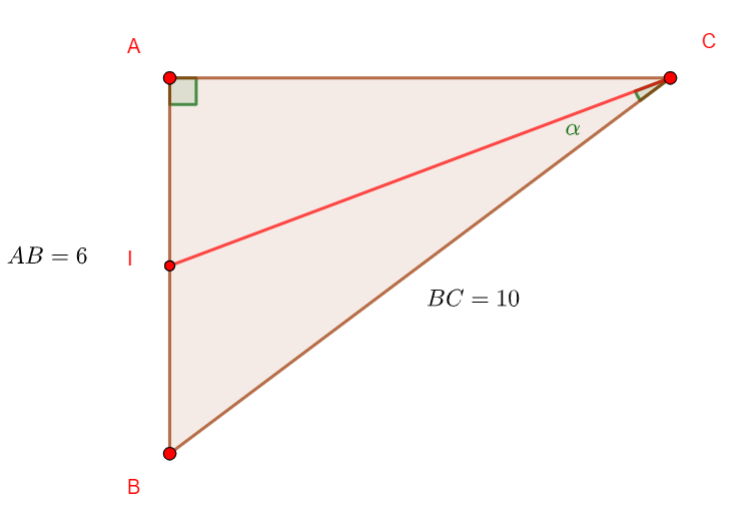
On considère la configuration suivante où I est le milieu de [AB].

  1. Calculer la distance AC.

Avant de se lancer dans les calculs, mesurer la distance AC à l’aide de la fenêtre active de géogébra ci-dessus.

Cliquer sur le 8ème onglet en haut à partir de la gauche, sélectionner Distance ou Longueur. Puis dans le repère cliquer successivement sur le point A et sur le point C. Le logiciel affiche la distance AC.

correction

2. Calculer la distance CI en utilisant la propriété de la médiane vue en exercice dans la leçon précédente:

A et B sont deux points du plan et I est le milieu de [AB].

Pour tout point M du plan, on a MA^2+MB^2=2MI^2+\frac{AB^2}{2}

Avant de se lancer dans les calculs, mesurer la distance CI à l’aide de la fenêtre active de géogébra ci-dessus.

Cliquer sur le 8ème onglet en haut à partir de la gauche, sélectionner Distance ou Longueur. Puis dans le repère cliquer successivement sur le point C et sur le point I. Le logiciel affiche la distance CI.

correction

3. Calculer la mesure en degrés de l’angle \widehat{ICB} noté \alpha sur la figure.

Avant de se lancer dans les calculs, mesurer l’angle  \widehat{ICB} à l’aide de la fenêtre active de géogébra ci-dessus.

Cliquer sur le 8ème onglet en haut à partir de la gauche, sélectionner Angle. Puis dans le repère cliquer successivement sur le point I, C et sur le point B. Le logiciel affiche la mesure en degrés de l’angle \widehat{ICB}.

correction

Exercice n°4

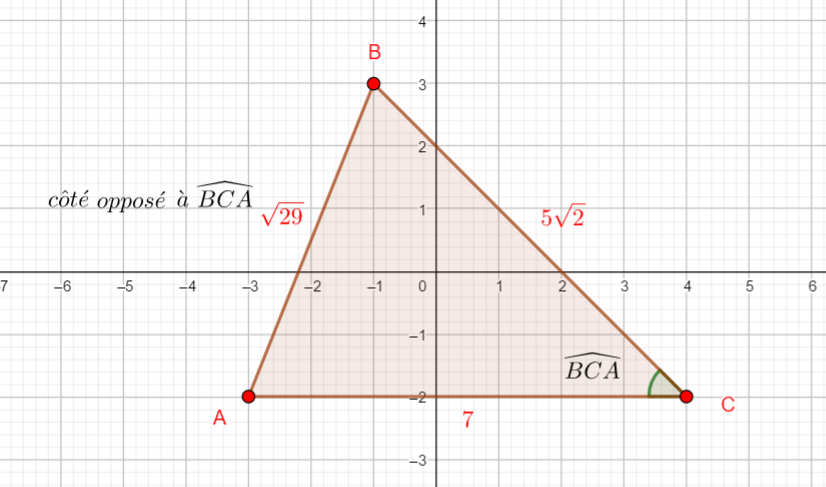
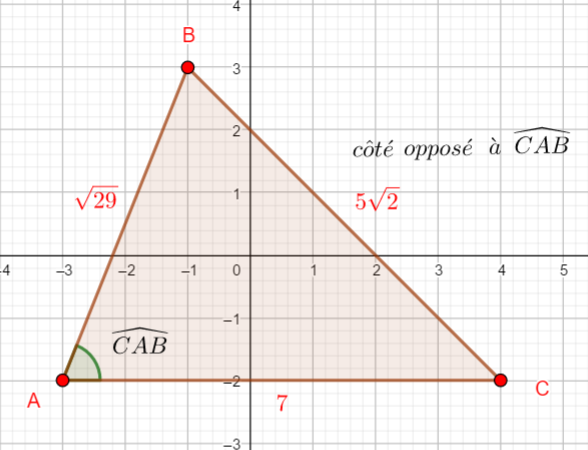
Dans un repère orthonormé, on considère les points suivants  A(-3;-2) , B(-1;3) et C(4;-2) .

  1. Calculer les distances AB , AC et BC.

Avant de se lancer dans les calculs, mesurer la distance AC à l’aide de la fenêtre active de géogébra ci-dessus.

Cliquer sur le 8ème onglet en haut à partir de la gauche, sélectionner Distance ou Longueur. Puis dans le repère cliquer successivement sur le point A et sur le point C. Le logiciel affiche la distance [latex]AC[/latex].

On peut aussi regarder dans la colonne de gauche, on voit écrit a=Segment(B,C,t1) et en dessous 7.07 qui est sa longueur.

correction AB
correction AC
correction BC

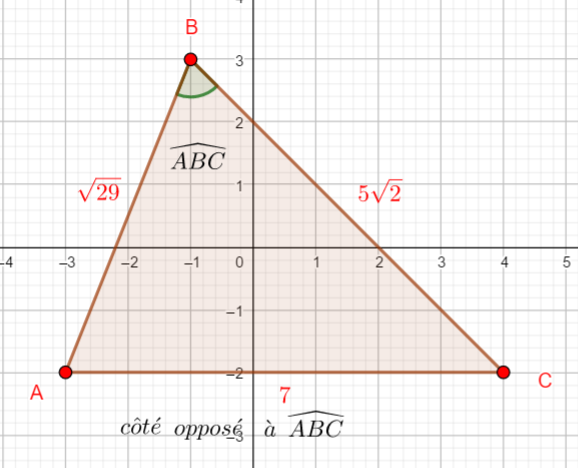
2. Calculer la mesure en degrés des angles \widehat{BCA} , \widehat{ABC} et \widehat{CAB}

Avant de se lancer dans les calculs, mesurer l’angle  \widehat{BCA} à l’aide de la fenêtre active de géogébra ci-dessus.

Cliquer sur le 8ème onglet en haut à partir de la gauche, sélectionner Angle. Puis dans le repère cliquer successivement sur le point B, C et sur le point A. Le logiciel affiche la mesure en degrés de l’angle \widehat{BCA}.

correction \widehat{BCA}
correction \widehat{ABC}
correction \widehat{CAB}(avec Al-Kashi)
correction \widehat{CAB}(plus simple)

©2020 – Math’O karé SAS

On utilise la formule où figure l’angle \widehat{ACB}\\ c^2=a^2+b^2-2\times a\times b\times cos(\widehat{ACB})

On remplace c par AB c’est-à-dire 4.

On remplace a par BC c’est-à-dire 5.

On remplace b par AC c’est-à-dire 6.

4^2=5^2+6^2-2\times 5\times 6\times cos(\widehat{ACB})

On calcule les puissances et les produits.

16=25+36-60 cos(\widehat{ACB})\\ 16=61-60 cos(\widehat{ACB})\\ 60 cos(\widehat{ACB})=61-16\\ 60 cos(\widehat{ACB})=45\\ cos(\widehat{ACB})=\frac{45}{60}\\ \widehat{ACB}=cos^{-1}(\frac{45}{60})\\ \widehat{ACB}=41°

 

 

On utilise la formule où figure l’angle \widehat{BAC}\\ a^2=b^2+c^2-2\times b\times c\times cos(\widehat{BAC})

On remplace b par AC c’est-à-dire 3.

On remplace c par AB c’est-à-dire 6.

On remplace \widehat{BAC} par 140°. 

a^2=3^2+6^2-2\times 3\times 6\times cos(140°)

On calcule les puissances et les produits.

a^2=9+36-36\times  (-0.766)\\ a^2=45+27.58\\ a^2=72.58\\ a=\sqrt{72.58}\\ a=8.5

Donc BC=8.5

 

 

cos(\widehat{ACB})=\frac{45}{60}\\ \widehat{ACB}=cos^{-1}(\frac{45}{60})\\ \widehat{ACB}=41°

Pour calculer la distance AC, on va appliquer le théorème de Pythagore dans le triangle rectangle ABC.

AB^2+AC^2=BC^2\\6^2+AC^2=10^2\\36+AC^2=100\\AC^2=64\\AC=\sqrt{64}\\AC=8

Pour calculer la distance CI, on va appliquer le théorème de la médiane dans le triangle  ABC où I est le milieu de [AB]\\CA^2+CB^2=2CI^2+\frac{AB^2}{2}\\8^2+10^2=2CI^2+\frac{6^2}{2}\\64+100=2CI^2+\frac{36}{2}\\164=2CI^2+18\\2CI^2+18=164\\2CI^2=164-18\\2CI^2=146\\CI^2=\frac{146}{2}\\CI^2=73\\CI=\sqrt{73}\\CI=8.5

Pour calculer  une mesure de l’angle \widehat{ICB} noté \alpha , on va appliquer le théorème d’Al Kashi dans le triangle  ICB. On le rappelle : 

c^2=a^2+b^2-2\times a\times b\times cos(\widehat{ACB})

IB^2=CB^2+CI^2-2\times CB\times CI\times cos(\widehat{ICB})\\ 3^2=10^2+73-2\times 10\times 8.5\times cos(\widehat{ICB})\\ 9=100+73-170 cos(\widehat{ICB})\\ 9=173-170 cos(\widehat{ICB})\\173-170 cos(\widehat{ICB})=9\\-170 cos(\widehat{ICB})=9-173\\-170 cos(\widehat{ICB})=-164\\ cos(\widehat{ICB})=\frac{-164}{-170}\\\widehat{ICB}=cos^{-1}(\frac{164}{170})\\\widehat{ICB}=15°

 

On n’hésite pas à repérer les coordonnées des points A et B ainsi

\hspace{0.6cm} x_{A} y_{A} \hspace{0.6cm} x_{B} y_{B}

\hspace{0.2cm} A(-3;-2) \hspace{0.4cm} B(-1;3)

On écrit la formule du cours :

AB=\sqrt {{(x_B-x_A) }^{2}+{(y_B-y_A) }^{2}} 

Et on prend soin de bien remplacer les lettres par les bons nombres. Dans le cas d’un nombre négatif, on le met entre parenthèses.

AB=\sqrt {{((-1)-(-3))}^{2}+{(3-(-2))}^{2}}

On calcule. On effectue d’abord ce qu’il y a entre parenthèses

AB=\sqrt {{2}^{2}+{5}^{2}} 

On effectue ensuite les puissances, ici les carrés. 

AB=\sqrt {4+25}

On effectue ensuite la somme

AB=\sqrt {29}

 

On n’hésite pas à repérer les coordonnées des points A et C ainsi

\hspace{0.6cm} x_{A} y_{A} \hspace{0.6cm} x_{C} y_{C}

\hspace{0.2cm} A(-3;-2) \hspace{0.4cm} C(4;-2)

On écrit la formule du cours :

AC=\sqrt {{(x_C-x_A) }^{2}+{(y_C-y_A) }^{2}} 

Et on prend soin de bien remplacer les lettres par les bons nombres. Dans le cas d’un nombre négatif, on le met entre parenthèses.

AC=\sqrt {{(4-(-3))}^{2}+{((-2)-(-2))}^{2}}

On calcule. On effectue d’abord ce qu’il y a entre parenthèses

AC=\sqrt {{7}^{2}+{0}^{2}} 

On effectue ensuite les puissances, ici les carrés. 

AC=\sqrt {49+0}

On effectue ensuite la somme

AC=\sqrt {49}

AC=7

 

On n’hésite pas à repérer les coordonnées des points B et C ainsi

\hspace{0.6cm} x_{B} y_{B} \hspace{0.6cm} x_{C} y_{C}

\hspace{0.2cm} B(-1;3) \hspace{0.4cm} C(4;-2)

On écrit la formule du cours :

BC=\sqrt {{(x_C-x_B) }^{2}+{(y_C-y_B) }^{2}} 

Et on prend soin de bien remplacer les lettres par les bons nombres. Dans le cas d’un nombre négatif, on le met entre parenthèses.

BC=\sqrt {{(4-(-1))}^{2}+{((-2)-3)}^{2}}

On calcule. On effectue d’abord ce qu’il y a entre parenthèses

BC=\sqrt {{5}^{2}+{(-5)}^{2}} 

On effectue ensuite les puissances, ici les carrés. 

BC=\sqrt {25+25}

On effectue ensuite la somme

BC=\sqrt {50}

Comme 50 peut s’écrire comme le produit d’un nombre fois le carré d’un nombre, on peut poursuivre.

BC=\sqrt {25\times 2}

BC=\sqrt {25}\times \sqrt{2}

BC=5\sqrt {2}

 

On veut déterminer une mesure de  l’angle \widehat{BCA} en utilisant Al Kashi.

Pour la formule, c’est facile. A gauche du signe égal, il y aura le carré du côté opposé à l’angle \widehat{BCA} ici AB.

A droite les carrés des côtés adjacents à l’angle ici AC et BC et l’opposé de leur double produit multiplié par cos( \widehat{BCA}).

AB^2=BC^2+AC^2-2\times BC\times AC\times cos(\widehat{BCA})

On remplace AB par  \sqrt{29}.

On remplace BC par 5\sqrt{2}.

On remplace AC par 7.

\sqrt{29}^2=(5\sqrt{2})^2+7^2-2\times 5\sqrt{2}\times 7\times cos(\widehat{BCA})

On calcule les puissances et les produits.

29=50+49- 70\sqrt{2}cos(\widehat{BCA})

29=99- 70\sqrt{2}cos(\widehat{BCA})

99- 70\sqrt{2}cos(\widehat{BCA})=29

– 70\sqrt{2}cos(\widehat{BCA})=29-99

– 70\sqrt{2}cos(\widehat{BCA})=-70

cos(\widehat{BCA})=\frac{-70}{-70\sqrt{2}}

\widehat{BCA}=cos^{-1}(\frac{1}{\sqrt{2}})

\widehat{BCA}=45°

 

On veut déterminer une mesure de  l’angle \widehat{ABC} en utilisant Al Kashi.

Pour la formule, c’est facile. A gauche du signe égal, il y aura le carré du côté opposé à l’angle \widehat{ABC} ici AC.

A droite les carrés des côtés adjacents à l’angle ici AB et BC et l’opposé de leur double produit multiplié par cos( \widehat{ABC}).

AC^2=BC^2+AB^2-2\times BC\times AB\times cos(\widehat{ABC})

On remplace AB par  \sqrt{29}.

On remplace BC par 5\sqrt{2}.

On remplace AC par 7.

7^2=(5\sqrt{2})^2+\sqrt{29}^2-2\times 5\sqrt{2}\times \sqrt{29}\times cos(\widehat{ABC})

On calcule les puissances et les produits.

49=50+29- 10\sqrt{58}cos(\widehat{ABC})

49=79- 10\sqrt{58}cos(\widehat{ABC})

79- 10\sqrt{58}cos(\widehat{ABC})=49

– 10\sqrt{58}cos(\widehat{ABC})=49-79

– 10\sqrt{58}cos(\widehat{ABC})=-30

cos(\widehat{ABC})=\frac{-30}{-10\sqrt{58}}

\widehat{ABC}=cos^{-1}(\frac{3}{\sqrt{58}})

\widehat{ABC}=67°

On veut déterminer une mesure de  l’angle \widehat{CAB} en utilisant Al Kashi.

Pour la formule, c’est facile. A gauche du signe égal, il y aura le carré du côté opposé à l’angle \widehat{BCA} ici BC.

A droite les carrés des côtés adjacents à l’angle ici AC et AB et l’opposé de leur double produit multiplié par cos( \widehat{CAB}).

BC^2=AB^2+AC^2-2\times AB\times AC\times cos(\widehat{CAB})

On remplace AB par  \sqrt{29}.

On remplace BC par 5\sqrt{2}.

On remplace AC par 7.

(5 \sqrt{2})^2=\sqrt{29}^2+7^2-2\times \sqrt{29}\times 7\times cos(\widehat{CAB})

On calcule les puissances et les produits.

50=29+49- 14\sqrt{29}cos(\widehat{CAB})

50=78- 14\sqrt{29}cos(\widehat{CAB})

78- 14\sqrt{29}cos(\widehat{CAB})=50

– 14\sqrt{29}cos(\widehat{CAB})=50-78

– 14\sqrt{29}cos(\widehat{CAB})=-28

cos(\widehat{CAB})=\frac{-28}{-14\sqrt{29}}

\widehat{CAB}=cos^{-1}(\frac{2}{\sqrt{29}})

\widehat{CAB}=68°

 

Dans un triangle, la somme des angles est égale à 180°, donc :

\widehat{BCA}+\widehat{ABC}+\widehat{CAB}=180\\45+67+\widehat{CAB}=180\\112+\widehat{CAB}=180\\\widehat{CAB}=180-112\\\widehat{CAB}=68°

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.