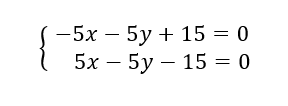logo

1. Produit scalaire. Exercices type évaluation de fin d’année.

Voici une fenêtre Géogébra pour traiter les exercices de la fiche. Si la fenêtre n’affiche pas les objets créés, utiliser le dernier onglet du haut à gauche qui est symbolisé par une croix. On peut ainsi modifier l’affichage du graphique.

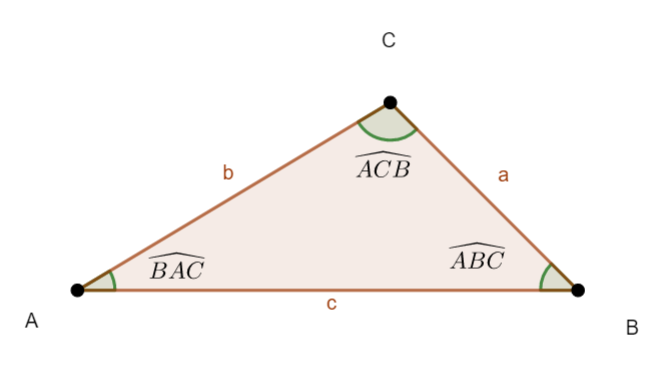
Exercice n°1

Le plan est muni d’un repère orthonormé .
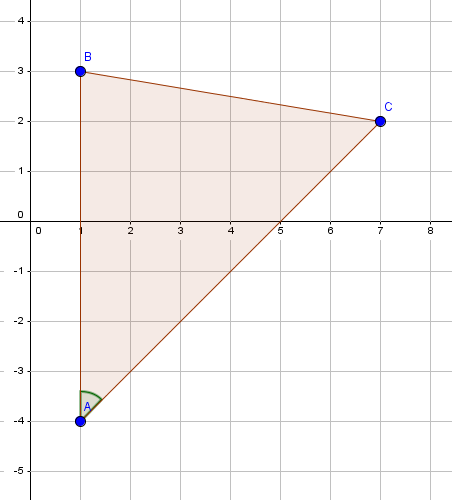
On considère les points : A(1;-4), B(1;3)  et C(7;2).

Utiliser la fenêtre géogébra ci-dessus.

Pour placer A, cliquer sur le 2ème onglet en haut à partir de la gauche, sélectionner Point dans le menu déroulant et dans le repère cliquer au point de coordonnées (1;-4).

Procéder de même pour B et C

1) Le triangle ABC est-il isocèle en B ?

Pour mesurer la distance  AB, cliquer sur le 8ème onglet en haut à partir de la gauche, sélectionner Distance ou longueur dans le menu déroulant et dans le repère cliquer sur le point A et sur le point B. La distance AB s’affiche.

Faire de même pour la distance BC.

Comparer les distances, on a conjecturé le résultat.

correction

2) En utilisant le théorème d’Al-Kashi, déterminer la valeur en degré de l’angle \widehat{CAB} .

Pour mesurer l’angle \widehat{CAB}, cliquer sur le 8ème onglet en haut à partir de la gauche, sélectionner Angle dans le menu déroulant et dans le repère cliquer sur le point C puis sur A et sur le point B. La mesure de l’angle  \widehat{CAB} s’affiche.

correction

3) On considère le point H de coordonnées (4.5;-0.5).
Le point H est-il le projeté orthogonal du point B sur la droite (AC) ?

Placer H dans le repère.

Tracer la droite (AC)

Pour tracer la perpendiculaire à (AC) passant par B, cliquer sur le 4ème onglet en haut à partir de la gauche, sélectionner Perpendiculaire dans le menu déroulant et dans le repère cliquer sur la droite (AC) et sur le point B.Passe-t-elle par H? On a conjecturé le résultat.

correction

Exercice n°2

On considère les points A(0;4), B(7;5) et C(9;1) dans un repère orthonormé.

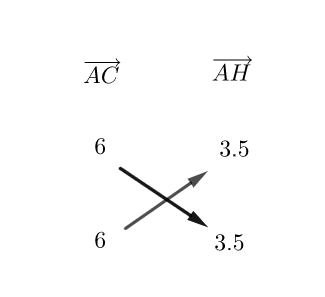
  1. a)Calculer les coordonnées des vecteurs \overrightarrow{AB} et \overrightarrow{AC}.

Pour tracer le vecteur \overrightarrow{AB} il faut  placer A et B puis cliquer sur le 3ème onglet en haut à partir de la gauche, sélectionner vecteur dans le menu déroulant et dans le repère cliquer sur le point  A puis sur le point B. Les coordonnées du vecteur apparaissent dans la colonne de gauche.

Procéder de même pour le vecteur \overrightarrow{AC}.

correction \overrightarrow{AB}
correction \overrightarrow{AC}

1.b)  En déduire le produit scalaire \overrightarrow{AB}.\overrightarrow{AC}

correction

2) On appelle D le projeté orthogonal du point B sur la droite (AC).

Pour placer le point D

tracer la droite  (AC) 

Cliquer sur le 3ème onglet en haut à partir de la gauche, sélectionner Droite dans le menu déroulant et dans le repère cliquer sur le point A et sur le point C. 

tracer la perpendiculaire à (AC) passant par B

Cliquer sur le 4ème onglet en haut à partir de la gauche, sélectionner Perpendiculaire dans le menu déroulant et dans le repère cliquer sur la droite (AC) et sur le point B. 

Construire le point d’intersection de cette perpendiculaire et de la droite (AC)

Cliquer sur le 2ème onglet en haut à partir de la gauche, sélectionner Intersection dans le menu déroulant et dans le repère cliquer sur la droite (AC) et sur la droite perpendiculaire tracée précédemment. Renommer le point. Les coordonnés du point d’intersection apparaît dans la colonne de gauche. 

a) A l’aide de la propriété avec la projection orthogonale, donner une expression du produit scalaire \overrightarrow{AB}.\overrightarrow{AC}

correction

    b) A l’aide des questions précédentes, calculer la distance AD.

Pour mesurer la distance  AD, cliquer sur le 8ème onglet en haut à partir de la gauche, sélectionner Distance ou longueur dans le menu déroulant et dans le repère cliquer sur le point A et sur le point D. La distance AD s’affiche.

correction

3) a) calculer la distance BD. 

Pour mesurer la distance  BD, cliquer sur le 8ème onglet en haut à partir de la gauche, sélectionner Distance ou longueur dans le menu déroulant et dans le repère cliquer sur le point B et sur le point D. La distance BD s’affiche.

correction

    b) calculer l’aire du triangle  ABC. 

Pour mesurer l’aire du triangle  ABC, il suffit de construire le polygone ABC. Cliquer sur le 5ème onglet en haut à partir de la gauche, sélectionner Polygone  dans le menu déroulant et dans le repère cliquer sur le point A, B, C et encore sur le point A. L’aire de  BABC apparaît dans la colonne de gauche sous Polygone A,B,C .

correction

Exercice 3

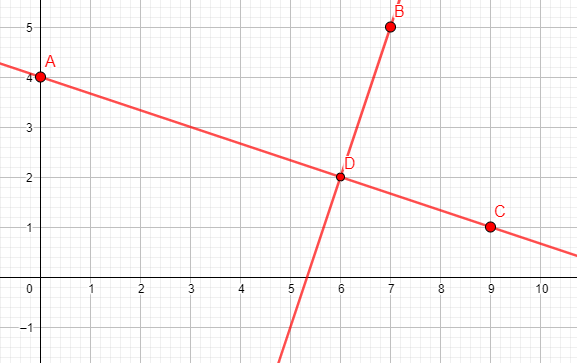
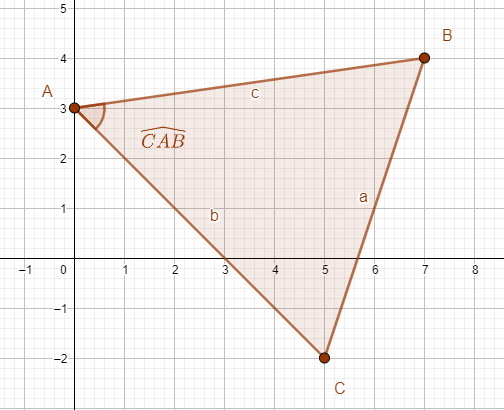
On considère les points A(0;3), B(7;4) et C(5;-2) dans un repère orthonormé.

1.a)Calculer les coordonnées des vecteurs \overrightarrow{AB} et \overrightarrow{AC}.

Pour tracer le vecteur \overrightarrow{AB} il faut  placer A et B puis cliquer sur le 3ème onglet en haut à partir de la gauche, sélectionner vecteur dans le menu déroulant et dans le repère cliquer sur le point  A puis sur le point B. Les coordonnées du vecteur apparaissent dans la colonne de gauche.

Procéder de même pour le vecteur \overrightarrow{AC}.

correction \overrightarrow{AB}
correction \overrightarrow{AC}

1.b)  En déduire le produit scalaire \overrightarrow{AB}.\overrightarrow{AC}

correction

1.c)  Calculer les distances AB et AC.

Pour mesurer la distance  AB, cliquer sur le 8ème onglet en haut à partir de la gauche, sélectionner Distance ou longueur dans le menu déroulant et dans le repère cliquer sur le point A et sur le point B. La distance AB s’affiche.

Idem pour AC

correction AB
correction AC

1.d) Déterminer une mesure de l’angle \widehat{BAC} au degré près.

Pour mesurer l’angle \widehat{BAC}, cliquer sur le 8ème onglet en haut à partir de la gauche, sélectionner Angle dans le menu déroulant et dans le repère cliquer sur le point B puis sur A et sur le point C. La mesure de l’angle  \widehat{BAC} s’affiche.

correction

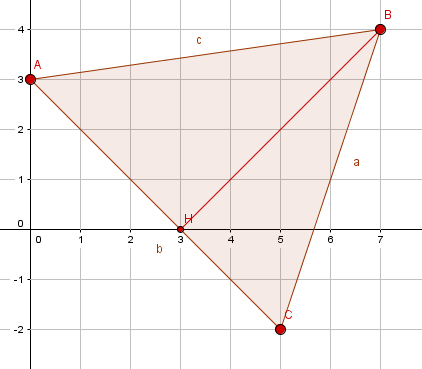
2. on note H le projeté orthogonal du point B sur la droite (AC).

Pour placer le point H

tracer la droite  (AC) 

Cliquer sur le 3ème onglet en haut à partir de la gauche, sélectionner Droite dans le menu déroulant et dans le repère cliquer sur le point A et sur le point C. 

tracer la perpendiculaire à (AC) passant par B

Cliquer sur le 4ème onglet en haut à partir de la gauche, sélectionner Perpendiculaire dans le menu déroulant et dans le repère cliquer sur la droite (AC) et sur le point B. 

Construire le point d’intersection de cette perpendiculaire et de la droite (AC)

Cliquer sur le 2ème onglet en haut à partir de la gauche, sélectionner Intersection dans le menu déroulant et dans le repère cliquer sur la droite (AC) et sur la droite perpendiculaire tracée précédemment. Renommer le point. Les coordonnés du point d’intersection apparaît dans la colonne de gauche. 

a) Déterminer une équation cartésienne de  (AC).

Pour tracer la droite (AC), cliquer sur le 3ème onglet en haut à partir de la gauche, sélectionner Droite dans le menu déroulant et dans le repère cliquer sur le point  A puis sur le point C. Une équation de la droite apparaît dans la colonne de gauche. Pout avoir une équation cartésienne, cliquer droit et sélectionner Equation ax+by+c=0.

correction

2.b) Montrer que  5x-5y-15=0 est une  équation cartésienne de  (BH).

Pour tracer la droite (BH), cliquer sur le 3ème onglet en haut à partir de la gauche, sélectionner Droite dans le menu déroulant et dans le repère cliquer sur le point  B puis sur le point H. Une équation de la droite apparaît dans la colonne de gauche. Pout avoir une équation cartésienne, cliquer droit et sélectionner Equation ax+by+c=0. Vérifier que cette équation est celle de l’énoncé ou une autre équation obtenue en multipliant celle de l’énoncé par un nombre.

correction

2.c) En déduire les coordonnées du point H.

correction
vérification TI-83 Premium

©2020 – Math’O karé SAS

On considère les points : A(1;-4), B(1;3). 

On n’hésite pas à repérer les coordonnées des points A et B ainsi

\hspace{0.6cm} x_{A} y_{A} \hspace{0.6cm} x_{B} y_{B}

\hspace{0.2cm} A(1;-4) \hspace{0.4cm} B(1;3)

On écrit la formule du cours :

AB=\sqrt {{(x_B-x_A) }^{2}+{(y_B-y_A) }^{2}} 

Et on prend soin de bien remplacer les lettres par les bons nombres. Dans le cas d’un nombre négatif, on le met entre parenthèses.

AB=\sqrt {{(1-1)}^{2}+{(3-(-4))}^{2}}

On calcule. On effectue d’abord ce qu’il y a entre parenthèses

AB=\sqrt {{0}^{2}+{7}^{2}} 

On effectue ensuite les puissances, ici les carrés. 

AB=\sqrt {0+49}

On effectue ensuite la somme

AB=\sqrt {49}

AB=7

On considère les points : B(1;3)  et C(7;2).

On n’hésite pas à repérer les coordonnées des points C et B ainsi

\hspace{0.6cm} x_{C} y_{C} \hspace{0.6cm} x_{B} y_{B}

\hspace{0.2cm} C(7;2) \hspace{0.4cm} B(1;3)

On écrit la formule du cours :

CB=\sqrt {{(x_B-x_C) }^{2}+{(y_B-y_C) }^{2}} 

Et on prend soin de bien remplacer les lettres par les bons nombres. Dans le cas d’un nombre négatif, on le met entre parenthèses.

CB=\sqrt {{(1-7)}^{2}+{(3-2)}^{2}}

On calcule. On effectue d’abord ce qu’il y a entre parenthèses

CB=\sqrt {{(-6)}^{2}+{1}^{2}} 

On effectue ensuite les puissances, ici les carrés. 

CB=\sqrt {36+1}

On effectue ensuite la somme

CB=\sqrt {37}

 

Comme AB\ne CB, le triangle ABC n’est pas isocèle en B.

 

 

Voici le théorème d’Al-Kashi 

Dans le triangle ABC ci-dessous

On a les égalités suivantes :

a^2=b^2+c^2-2\times b\times c\times cos(\widehat{BAC})

b^2=a^2+c^2-2\times a\times c\times cos(\widehat{ABC})

c^2=a^2+b^2-2\times a\times b\times cos(\widehat{ACB})

En examinant la figure ci-dessous et la question posée, il faut utiliser l’égalité n°1.

a^2=b^2+c^2-2\times b\times c\times cos(\widehat{BAC}) s’écrit aussi

BC^2=AC^2+AB^2-2\times AC\times AB\times cos(\widehat{BAC})

On a montré précédemment que BA=7 et BC=\sqrt{37}.

Il faut maintenant calculer AC

On n’hésite pas à repérer les coordonnées des points A et C ainsi

\hspace{0.6cm} x_{A} y_{A} \hspace{0.6cm} x_{C} y_{C}

\hspace{0.2cm} A(1;-4) \hspace{0.4cm} C(7;2)

On écrit la formule du cours :

AC=\sqrt {{(x_C-x_A) }^{2}+{(y_C-y_A) }^{2}} 

Et on prend soin de bien remplacer les lettres par les bons nombres. Dans le cas d’un nombre négatif, on le met entre parenthèses.

AC=\sqrt {{(7-1)}^{2}+{(2-(-4))}^{2}}

On calcule. On effectue d’abord ce qu’il y a entre parenthèses

AC=\sqrt {{6}^{2}+{6}^{2}} 

On effectue ensuite les puissances, ici les carrés. 

AC=\sqrt {36+36}

On effectue ensuite la somme

AC=\sqrt {72}

Pour finir, on regarde si on peut écrire 72 comme le produit d’un nombre de du carré d’un nombre. Ici 72={2}\times{{6}^{2}}

AC=\sqrt {{2}\times{{6}^{2}}}

On applique ensuite la règle suivante : \sqrt{a\times b}=\sqrt{a}\times\sqrt{b}

AB={\sqrt{2}}\times{\sqrt{{6}^{2}}}

Il ne reste plus qu’à appliquer la règle suivante : si a est positif ou nul alors \sqrt {{a}^{2}}=a

AC=6\sqrt {2}

On remplace BC par \sqrt{37},  AC par 6\sqrt {2} et AB par 7 dans BC^2=AC^2+AB^2-2\times AC\times AB\times cos(\widehat{BAC})

\sqrt{37}^2=(6\sqrt {2})^2+7^2-2\times 6\sqrt {2}\times 7\times cos(\widehat{BAC})\\37=72+49-2\times 6\sqrt {2}\times 7\times cos(\widehat{BAC})\\72+49-2\times 6\sqrt {2}\times 7\times cos(\widehat{BAC})=37\\121-84\sqrt {2} cos(\widehat{BAC})=37\\-84\sqrt {2} cos(\widehat{BAC})=37-121\\-84\sqrt {2} cos(\widehat{BAC})=-84\\ cos(\widehat{BAC})=\frac{-84}{-84\sqrt {2}}\\ cos(\widehat{BAC})=\frac{1}{\sqrt {2}}

En utilisant la calculatrice avec la touche cos^{-1}, on obtient :

la mesure de \widehat{BAC} est 45°.

 

On considère le point H de coordonnées (4.5;-0.5).
Le point H est-il le projeté orthogonal du point B sur la droite (AC) ?

étape n°1 : Il faut d’abord montrer que le point H est sur la droite (AC).

Pour cela calculons, par exemple, les coordonnées des vecteurs \overrightarrow{AC} et \overrightarrow{AH} et montrons que leur déterminant est nul.

Pour déterminer les coordonnées du vecteur \overrightarrow{AC}.

Je repère les coordonnées des points A et C.

\hspace{0.3cm}x_{A}\hspace{0.2cm}y_{A}\hspace{2cm}x_{C}\hspace{0.2cm}y_{C}

A(1;-4)\hspace{2cm}C(7;2)

J’écris la formule : \overrightarrow{AC}(x_{C}-x_{A};y_{C}-y_{A})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{AC}(7-1;2-(-4))

\overrightarrow{AC}(6;2+4)

\overrightarrow{AC}(6;6)

Pour déterminer les coordonnées du vecteur \overrightarrow{AH}.

Je repère les coordonnées des points A et H.

\hspace{0.3cm}x_{A}\hspace{0.2cm}y_{A}\hspace{2.6cm}x_{H}\hspace{0.2cm}y_{H}

A(1;-4)\hspace{2cm}H(4.5;-0.5)

J’écris la formule : \overrightarrow{AH}(x_{H}-x_{A};y_{H}-y_{A})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{AH}(4.5-1;-0.5-(-4))

\overrightarrow{AH}(3.5;-0.5+4)

\overrightarrow{AH}(3.5;3.5)

J’utilise la disposition pratique ci-dessous pour calculer det(\overrightarrow{AC};\overrightarrow{AH})  

det(\overrightarrow{AC};\overrightarrow{AH}) ={6}\times{3.5}-{6}\times{3.5} 

det(\overrightarrow{AC};\overrightarrow{AH}) =0 

Donc les vecteurs \overrightarrow{AC} et \overrightarrow{AH} sont colinéaires donc H est sur la droite (AC).

étape n°2 : Il faut d’abord montrer que les droites (AC) et (BH) sont perpendiculaires.

Pour cela calculons, par exemple, les coordonnées des vecteurs \overrightarrow{AC} et \overrightarrow{BH} et montrons que leur produit scalaire est nul.

On a déjà calculé les coordonnées du vecteur \overrightarrow{AC}, il n’y a plus qu’à calculer les coordonnées du vecteur \overrightarrow{BH}.

 

Pour déterminer les coordonnées du vecteur \overrightarrow{BH}.

Je repère les coordonnées des points B et H.

\hspace{0.3cm}x_{B}\hspace{0.2cm}y_{B}\hspace{2.6cm}x_{H}\hspace{0.2cm}y_{H}

B(1;3)\hspace{2cm}H(4.5;-0.5)

J’écris la formule : \overrightarrow{BH}(x_{H}-x_{B};y_{H}-y_{B})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{BH}(4.5-1;-0.5-3)

\overrightarrow{BH}(3.5;-3.5)

On calcule le produit scalaire en utilisant la forme analytique 

\overrightarrow{AC}\overrightarrow{BH}=6\times 3.5+6\times (- 3.5)

\overrightarrow{AC}\overrightarrow{BH}=21-21

\overrightarrow{AC}\overrightarrow{BH}=0

Donc les vecteurs \overrightarrow{AC} et \overrightarrow{BH} sont orthogonaux donc les droites (AC) et (BH) sont perpendiculaires.

On a donc montré que H est le projeté orthogonal de B sur la droite (AC).

 

 

Pour déterminer les coordonnées du vecteur \overrightarrow{AB}.

Je repère les coordonnées des points A et B.

\hspace{2.1cm}x_{A}\hspace{0.2cm}y_{A}\hspace{2cm}x_{B}\hspace{0.2cm}y_{B}

\hspace{1.8cm}A(0;4)\hspace{2cm}B(7;5)

J’écris la formule : \overrightarrow{AB}(x_{B}-x_{A};y_{B}-y_{A})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{AB}(7-0;5-4)

\overrightarrow{AB}(7;1)

 

Pour déterminer les coordonnées du vecteur \overrightarrow{AC}.

Je repère les coordonnées des points A et C.

\hspace{2.1cm}x_{A}\hspace{0.2cm}y_{A}\hspace{2cm}x_{C}\hspace{0.2cm}y_{C}

\hspace{1.8cm}A(0;4)\hspace{2cm}C(9;1)

J’écris la formule : \overrightarrow{AC}(x_{C}-x_{A};y_{C}-y_{A})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{AC}(9-0;1-4)

\overrightarrow{AC}(9;-3)

On a vu que \overrightarrow{AB}(7;1) et que \overrightarrow{AC}(9;-3).

Pour calculer le produit scalaire \overrightarrow{AB}.\overrightarrow{AC}, on va utiliser xx’+yy’ en remplaçant x par 7 , y par 1 , x’ par 9 et y’ par (-3).

\overrightarrow{AB}.\overrightarrow{AC}=7\times 9+1\times (-3)

\hspace{1.3cm}=63-3

\hspace{1.3cm}=60

Voici la figure : 

Pour calculer \overrightarrow{AB}.\overrightarrow{AC} avec la projection, on choisit, compte-tenu de l’énoncé,  de projeter les points  A et B du premier vecteur \overrightarrow{AB} sur la droite (AC) qui correspond au deuxième vecteur \overrightarrow{AC}.

\overrightarrow{AB}.\overrightarrow{AC}=AD.AC car \overrightarrow{AD} et \overrightarrow{AC} ont même sens.

Dans la question 1b, on a obtenu \overrightarrow{AB}.\overrightarrow{AC}=60

Dans la question 2.a on a obtenu \overrightarrow{AB}.\overrightarrow{AC}=AD.AC

Donc AD.AC=60

Calculons la distance AC en utilisant la formule du cours suivante AC^2=\overrightarrow{AC}^2\\AC^2=\overrightarrow{AC}.\overrightarrow{AC}

Pour calculer \overrightarrow{AC}.\overrightarrow{AC}, on utilise xx’+yy’ en remplaçant x et x’ par 9 et y et y’ par (-3).

AC^2=9\times 9+(-3)\times (-3)\\AC^2=81+9\\AC^2=90\\AC=\sqrt{90}\\AC=\sqrt{9\times 10}\\AC=\sqrt{9}\times \sqrt{10}\\AC=3\sqrt{10}

On remplace AC par 3\sqrt{10} dans AD.AC=60.

AD\times 3\sqrt{10}=60

AD=\frac{60}{3\sqrt{10}}

AD=\frac{20}{\sqrt{10}}

Il n’est pas très élégant de laisser une racine au dénominateur donc on multiplie en haut et en bas par \sqrt{10}.

AD={\frac{20}{\sqrt{10}}}\times {\frac{\sqrt{10}}{\sqrt{10}}}

AD=\frac{20\sqrt{10}}{10}

AD=2\sqrt{10}

Voici la figure

Pour déterminer l’aire du triangle, on choisit une base et sa hauteur correspondante.

D’après l’énoncé, on va choisir [AC] comme base et  [BD] comme hauteur.

Aire de [ABC] vaut \frac{AC\times BD}{2}.

On remplace AC par 3\sqrt{10} et BD par \sqrt{10} dans \frac{AC\times BD}{2}.

Aire de [ABC] vaut

\frac{3\sqrt{10}\times \sqrt{10}}{2}=\frac{3\times 10}{2}

\hspace{1.45cm}=3\times 5

\hspace{1.45cm}=15

 

Pour déterminer les coordonnées du vecteur \overrightarrow{AB}.

Je repère les coordonnées des points A et B.

\hspace{2.1cm}x_{A}\hspace{0.2cm}y_{A}\hspace{2cm}x_{B}\hspace{0.2cm}y_{B}

\hspace{1.8cm}A(0;3)\hspace{2cm}B(7;4)

J’écris la formule : \overrightarrow{AB}(x_{B}-x_{A};y_{B}-y_{A})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{AB}(7-0;4-3)

\overrightarrow{AB}(7;1)

Pour déterminer les coordonnées du vecteur \overrightarrow{AC}.

Je repère les coordonnées des points A et C.

\hspace{2.1cm}x_{A}\hspace{0.2cm}y_{A}\hspace{2cm}x_{C}\hspace{0.2cm}y_{C}

\hspace{1.8cm}A(0;3)\hspace{2cm}C(5;-2)

J’écris la formule : \overrightarrow{AC}(x_{C}-x_{A};y_{C}-y_{A})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{AC}(5-0;(-2)-3)

\overrightarrow{AC}(5;-5)

On a vu que \overrightarrow{AB}(7;1) et que \overrightarrow{AC}(5;-5).

Pour calculer le produit scalaire \overrightarrow{AB}.\overrightarrow{AC}, on va utiliser xx’+yy’ en remplaçant x par 7 , y par 1 , x’ par 5 et y’ par (-5).

\overrightarrow{AB}.\overrightarrow{AC}=7\times 5+1\times (-5)

\hspace{1.3cm}=35-5

\hspace{1.3cm}=30

Calculons la distance AB en utilisant la formule du cours suivante AB^2=\overrightarrow{AB}^2\\AB^2=\overrightarrow{AB}.\overrightarrow{AB}

Pour calculer \overrightarrow{AB}.\overrightarrow{AB}, on utilise xx’+yy’ en remplaçant x et x’ par 7 et y et y’ par 1.

AB^2=7\times 7+1\times 1\\AB^2=49+1\\AB^2=50\\AB=\sqrt{50}\\AB=\sqrt{25\times 2}\\AB=\sqrt{25}\times \sqrt{2}\\AB=5\sqrt{2}

Calculons la distance AC en utilisant la formule du cours suivante AC^2=\overrightarrow{AC}^2\\AC^2=\overrightarrow{AC}.\overrightarrow{AC}

Pour calculer \overrightarrow{AC}.\overrightarrow{AC}, on utilise xx’+yy’ en remplaçant x et x’ par 5 et y et y’ par (-5).

AC^2=5\times 5+(-5)\times (-5)\\AC^2=25+25\\AC^2=50\\AC=\sqrt{50}\\AC=\sqrt{25\times 2}\\AC=\sqrt{25}\times \sqrt{2}\\AC=5\sqrt{2}

Voici le théorème d’Al-Kashi 

Dans le triangle ABC ci-dessous

On a les égalités suivantes :

a^2=b^2+c^2-2\times b\times c\times cos(\widehat{BAC})

b^2=a^2+c^2-2\times a\times c\times cos(\widehat{ABC})

c^2=a^2+b^2-2\times a\times b\times cos(\widehat{ACB})

En examinant la figure ci-dessous et la question posée, il faut utiliser l’égalité n°1.

a^2=b^2+c^2-2\times b\times c\times cos(\widehat{CAB}) s’écrit aussi

BC^2=AC^2+AB^2-2\times AC\times AB\times cos(\widehat{CAB})

On a montré précédemment que AB=5\sqrt{2} et AC=5\sqrt{2}.

Calculons la distance BC en utilisant la formule du cours suivante BC^2=\overrightarrow{BC}^2\\BC^2=\overrightarrow{BC}.\overrightarrow{BC}

Pour calculer \overrightarrow{BC}.\overrightarrow{BC}, on utilise xx’+yy’ en remplaçant x et x’ par l’abscisse du vecteur \overrightarrow{BC} :  x_C-x_B=5-7=-2 et y et y’ par l’ordonnée du vecteur \overrightarrow{BC} : y_C-y_B=-2-4=-6.

BC^2=(-2)\times (-2)+(-6)\times (-6)\\BC^2=4+36\\BC^2=40\\BC=\sqrt{40}\\BC=\sqrt{4\times 10}\\BC=\sqrt{4}\times \sqrt{10}\\BC=2\sqrt{10}

On remplace BC par 2\sqrt{10},  AC par 5\sqrt {2} et AB par 5\sqrt {2} dans

BC^2=AC^2+AB^2-2\times AC\times AB\times cos(\widehat{BAC})

(2\sqrt{10})^2=(5\sqrt {2})^2+(5\sqrt {2})^2-2\times (5\sqrt {2})\times (5\sqrt {2})\times cos(\widehat{CAB})\\40=50+50-2\times 25\times 2\times cos(\widehat{CAB})\\50+50-2\times 25\times 2\times cos(\widehat{CAB})=40\\100-100 cos(\widehat{CAB})=40\\-100 cos(\widehat{CAB})=40-100\\-100 cos(\widehat{CAB})=-60\\ cos(\widehat{CAB})=\frac{-60}{-100}\\ cos(\widehat{CAB})=\frac{3}{5}

En utilisant la calculatrice avec la touche cos^{-1}, on obtient :

la mesure de \widehat{CAB} est 53°.

 

Déterminer par le calcul une équation cartésienne de la  droite (AC) qui passe par  A (0;3) et C (5;-2) .

Il s’agit de déterminer une relation du type ax+by+c=0.

On sait que  \overrightarrow{AC}(5;-5)

Le vecteur \overrightarrow{AC} (5;-5) est un vecteur directeur de (AC) .

On sait , d’après le cours , que le  vecteur de coordonnées (-b;a) est un vecteur directeur de la droite D d’équation ax+by+c=0 .

Donc ici  -b=5 et  a=-5.

Ou encore b=-5 et  a=-5.

Donc l’équation cartésienne de (AC) est de la forme {(-5)}\times{x}+{(-5)}\times{y}+c=0.

Ou plus simplement -5x-5y+c=0.

Pour déterminer c, il suffit de remplacer x et y par les coordonnées du point A c’est-à-dire 0 et 3.

{(-5)}\times{0}+{(-5)}\times{3}+c=0\\-15+c=0\\c=15

Une équation de la droite (AC) est -5x-5y+15=0.

Remarque : si on divise par -5, on obtient une autre équation de la droite (AC) dont l’écriture est allégée : x+y-3=0.

C’est d’ailleurs celle qui est donnée par le logiciel Géogébra.

Voici la figure

 On veut montrer que  5x-5y-15=0 est une  équation cartésienne de  (BH).

Un vecteur directeur \overrightarrow{v}de (BH) a pour coordonnées (5;5). On a déjà montré que \overrightarrow{AC}(5;-5) 

On calcule le produit scalaire \overrightarrow{AC}.\overrightarrow{v} à l’aide de  xx’+yy’ en remplaçant x par 5, y par -5, x’ par 5 et y’ par 5.

\overrightarrow{AC}.\overrightarrow{v}=5\times 5+(-5)\times 5

\hspace{1.1cm}=25-25

\hspace{1.1cm}=0

Donc les vecteurs \overrightarrow{AC} et \overrightarrow{v} sont orthogonaux.

Donc 5x-5y-15=0 est une  équation cartésienne d’une droite perpendiculaire à la droite  (AC).

On remplace x et y par les coordonnées de B c’est-à-dire 7 et 4 dans l’équation 5x-5y-15=0.

5\times 7-5\times 4-15=35-20-15=0 donc les coordonnées du point B vérifient l’équation 5x-5y-15=0.

La droite d‘équation 5x-5y-15=0 passe par B.

On a montré que la droite d‘équation 5x-5y-15=0 passe par  B et est perpendiculaire à la droite  (AC), c’est donc la droite (BH).

 

 

Il s’agit de résoudre par le calcul et par combinaison linéaire, le système suivant :

Je décide d’éliminer les x , pour cela j’ajoute les deux équations.

-5x-5y+15+5x-5y-15=0\\-10y=0

-7 n’est pas à sa place dans le membre de gauche, c’est un facteur dans un produit. On divise par-10 de chaque côté.

y=\frac{0}{-10}\\y=0

Pour déterminer la valeur de x  je remplace y par 0  dans par exemple la première équation de départ.

-5x-{5}\times{0}+15=0\\-5x+15=0

15 n’est pas à sa place dans le membre de gauche, c’est un terme dans une somme. On enlève   15 de chaque côté.

-5x=0-15\\-5x=-15

-5 n’est pas à sa place dans le membre de gauche, c’est un facteur dans un produit. On divise par-5 de chaque côté.

x=\frac{-15}{-5}\\x=3

Donc le point H a pour coordonnées x=3 et y=0. Donc H(3;0).

 

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.