Dans un repère orthonormé, on considère les points suivants A(-4;-1) , B(-1;3) et C(3;1).
La fenêtre Géogébra est active, utilisez-la à bon escient.
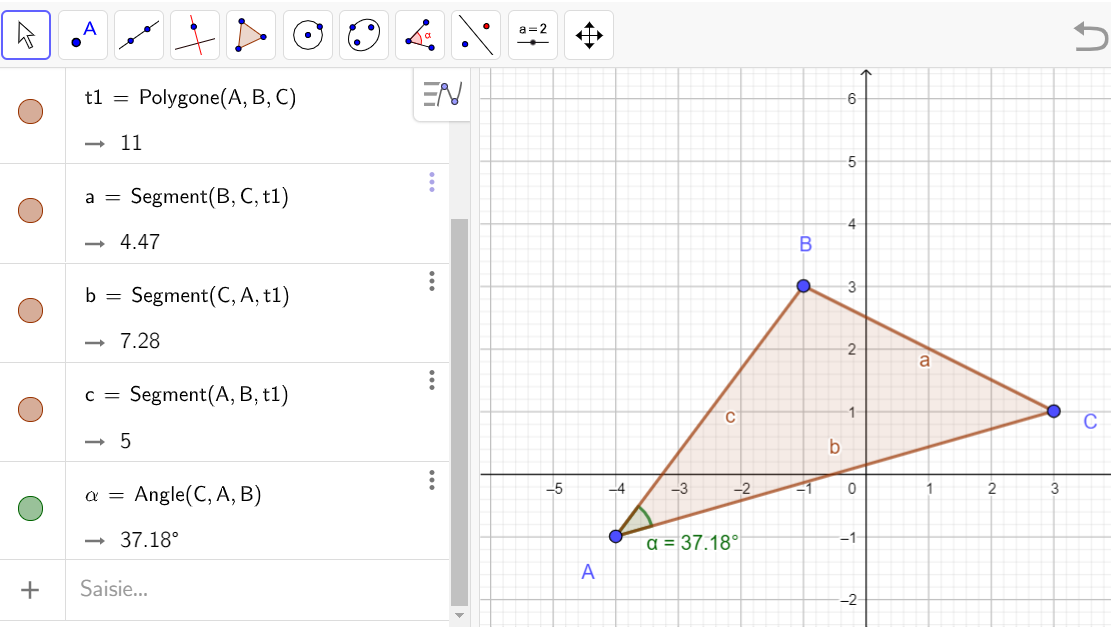
- Calculer les distances AB , AC et BC.
Avant de se lancer dans les calculs, mesurer la distance AB à l’aide de la fenêtre active de géogébra ci-dessus.
Cliquer sur le 8ème onglet en haut à partir de la gauche, sélectionner Distance ou Longueur. Puis dans le repère cliquer successivement sur le point A et sur le point B. Le logiciel affiche la distance [latex]AB[/latex].
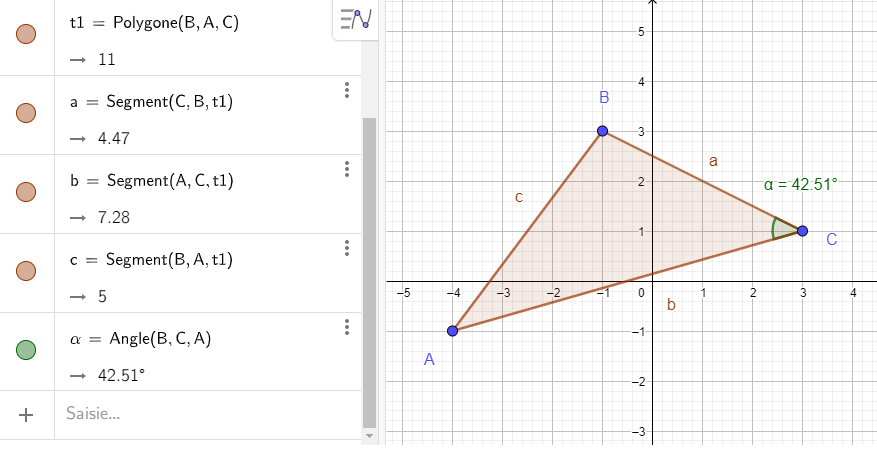
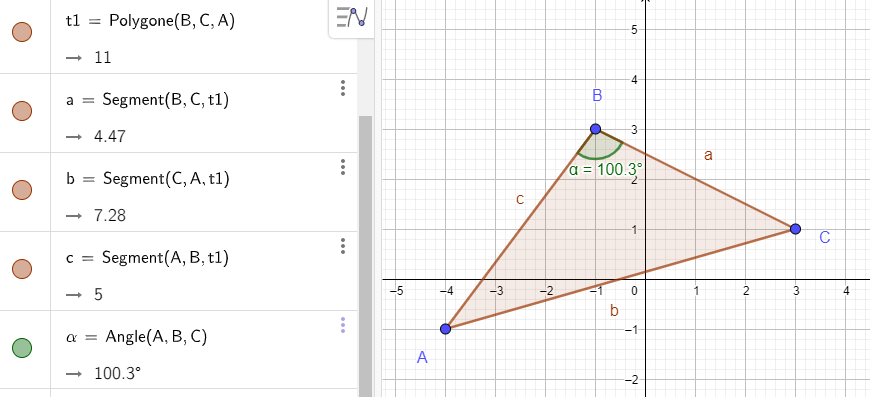
2. Calculer la mesure en degrés des angles \widehat{BCA} , \widehat{ABC} et \widehat{CAB}
Avant de se lancer dans les calculs, mesurer l’angle \widehat{BCA} à l’aide de la fenêtre active de géogébra ci-dessus.
Cliquer sur le 8ème onglet en haut à partir de la gauche, sélectionner Angle. Puis dans le repère cliquer successivement sur le point B, sur le point C et sur le point A. Le logiciel affiche la mesure en degrés de l’angle \widehat{BCA}.