logo

1. Somme de termes de suite arithmétique ou géométrique.

Sommaire

Somme de termes consécutifs d’une suite arithmétique

Activité : « le p’tit Gauss ».

Il paraîtrait qu’à l’âge de 7 ans, Gauss aurait calculé la somme des nombres entiers de 1 à 100 très rapidement alors que le maître avait donné cet exercice en pensant occuper sa classe un bon moment. Voilà comment il s’y ait pris : Gauss additionne 1 avec 100, puis 2 avec 99, puis 3 avec 98 et ainsi de suite jusqu’à 50 avec 51. Il obtient une somme de 50 fois la valeur 101, soit 5 050. 

  1. Calculer la somme des entiers naturels de 1 à 200 en s’inspirant de la méthode de Gauss.
correction

2. Calculer la somme des entiers naturels de 1 à 301 en s’inspirant de la méthode de Gauss.

correction

3. Exprimer la somme des entiers naturels de 1 à p en fonction de p en s’inspirant de la méthode de Gauss.

correction

Propriété n°1

Pour tout entier naturel n ,  1+2+3+…+n=\frac{n(n+1)}{2}.

On écrit : \sum_{k=1}^n k=\frac{n(n+1)}{2}.

Prolongement

On considère une suite arithmétique de premier terme u_0 et de raison r. On se propose d’exprimer S, la somme des n+1 premiers termes consécutifs de la suite (u_n), c’est-à-dire S=u_0+u_1+u_2+u_3+…+u_n.

1.En utilisant la définition explicite d’une suite arithmétique de premier terme u_0 et de raison r. Exprimer u_n en fonction de n et de r. Puis exprimer u_0+u_n en fonction de n et de r

correction

2.En utilisant la définition explicite d’une suite arithmétique de premier terme u_0 et de raison r. Exprimer u_1 en fonction de u_0 et de r,exprimer u_{n-1} en fonction de u_0, de n et de r  Puis exprimer u_1+u_{n-1} en fonction de u_0, de n et de r.

correction

3.En utilisant la définition explicite d’une suite arithmétique de premier terme u_0 et de raison r. Exprimer u_2 en fonction de u_0 et de r,exprimer u_{n-2} en fonction de u_0, de n et de r  Puis exprimer u_2+u_{n-2} en fonction de u_0, de n et de r.

correction

4. Que peut-on conclure par rapport aux questions précédentes? Peut-on envisager de remplacer tous les termes de la suite par  \frac{u_0+u_n}{2}? Montrer alors que  S=(n+1)\frac{u_0+u_n}{2}

correction

Propriété n°2

On considère une suite arithmétique de  raison r. On note S, la somme des n+1 premiers termes consécutifs de la suite (u_n), c’est-à-dire S=u_0+u_1+u_2+u_3+…+u_n.

On a S=(n+1)\frac{u_0+u_n}{2}

De façon plus générale :

S= nombre \hspace{0.2cm}de \hspace{0.2cm} termes \times  \frac{premier\hspace{0.2cm}terme \hspace{0.2cm} +\hspace{0.2cm} dernier \hspace{0.2cm}terme}{2}

Remarque

La deuxième formule est plus générale, elle permet de calculer la somme de termes consécutifs d’une suite arithmétique sans pour autant que le premier terme soit u_0.

Exemple n°1 

On veut calculer 5+7+9+11+13+15+17+19+21.

C’est une suite arithmétique de raison 2.

Le premier terme est 5

Le dernier terme est 21.

1.Conjecturer avec la calculatrice TI-83 Premium

L’écriture explicite de la suite est u_n=u_0+n\times r.

\hspace{4.2cm}u_n=5+2\times n.

De plus 21=5+2\times 8 donc c’est u_8.

2. Conjecturer avec l’application Tableur de Géogébra.

Saisir le premier terme est 5 dans la cellule A1.

Saisir la formule =A1+2 dans la cellule A2 et recopier vers le bas jusqu’à obtenir 21.

Sélectionner la plage allant de A1 à A9 et cliquer sur l’onglet \sum. parfois, il est plus facile de saisir dans la case vide qui suit le dernier terme =Somme(A1:A9).

C’est une suite arithmétique de raison 2.

Le premier terme est 5

Le dernier terme est 21.

Pour trouver le nombre de termes on calcule 21-5=16, on divise par la raison 2 :  \frac{16}{2}=8 et on ajoute le nombre 1  :  8+1=9. Il y a donc 9 termes.

On calcule à l’aide de la formule suivante :

S= nombre \hspace{0.2cm}de \hspace{0.2cm} termes \times  \frac{premier\hspace{0.2cm}terme \hspace{0.2cm} +\hspace{0.2cm} dernier \hspace{0.2cm}terme}{2}

S=9\times \frac{5+21}{2}\\S=9\times \frac{26}{2}\\S=9\times 13\\S=117

Exercice n°1

Calculer les sommes suivantes composées de termes consécutifs d’une suite arithmétique.

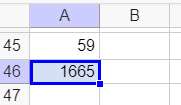
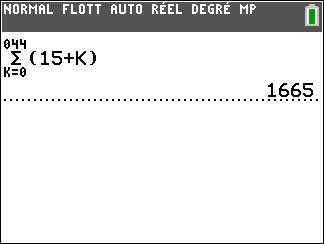
1.S_1=15+16+17+….+57+58+59

correction

2.S_2=15+20+25+….+155+160+165

correction

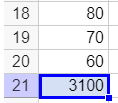
3.S_3=250+240+230+….+80+70+60

correction

Exemple n°2 

(u_n) est une suite arithmétique de premier terme u_0=-10 et de raison  r=5.

On veut calculer S=u_0+u_1+u_2+…+u_8.

Conjecturer avec l’application Calcul Formel de Géogébra.

Saisir sur la ligne n°1 Somme(-10+5n,n, 0,8) et valider avec entrée. Le logiciel affiche la valeur 90

Le premier terme est u_0, c’est-à-dire -10.

Le dernier terme est u_8=-10+8\times 5=30.

De u_0 à u_8, il y a 9 termes.

On calcule à l’aide de la formule suivante :

S= nombre \hspace{0.2cm}de \hspace{0.2cm} termes \times  \frac{premier\hspace{0.2cm}terme \hspace{0.2cm} +\hspace{0.2cm} dernier \hspace{0.2cm}terme}{2}

S=9\times \frac{-10+30}{2}\\S=9\times \frac{20}{2}\\S=9\times 10\\S=90

Exercice n°2

Calculer la somme S dans chaque cas.

1. (u_n) est une suite arithmétique de premier terme u_0=2 et de raison  r=3.

Calculer S=u_0+u_1+u_2+…+u_{12}.

correction

2. (u_n) est une suite arithmétique de premier terme u_0=-3 et vérifiant u_{n+1}=u_n+2.

Calculer S=u_2+u_3+u_4+…+u_{15}.

correction

3. (u_n) est une suite arithmétique définie par  u_n=-1+5n.

Calculer S=u_1+u_2+u_3+…+u_{20}.

correction

Somme de termes consécutifs d’une suite géométrique

Activité :

On se propose d’exprimer la somme S=1+q^2+q^3+…q^n fonction de q et de n.

  1. Multiplier l’égalité S=1+q^2+q^3+…q^n par -q de chaque côté. .
correction

2. Ajouter membre à membre l’égalité de l’énoncé et celle obtenue à la question n°1

correction

3. Après avoir mis S en facteur dans le membre de gauche de l’égalité obtenue à la question n°2, exprimer S en fonction de q et de n .

correction

Propriété n°3

Pour tout entier naturel n non nul, et pour q différent de 1 ,

1+q+q^2+q^3+…+q^n=\frac{1-q^{n+1}}{1-q}.

On écrit : \sum_{k=0}^n q^k=\frac{1-q^{n+1}}{1-q}.

Prolongement

On considère une suite géométrique de premier terme u_0 et de raison q. On se propose d’exprimer S, la somme des n+1 premiers termes consécutifs de la suite (u_n), c’est-à-dire S=u_0+u_1+u_2+u_3+…+u_n en fonction de q et de n.

  1. En utilisant la définition explicite d’une suite géométrique de premier terme u_0 et de raison q. Exprimer u_1, u_2, u_3 et u_n en fonction de q et de leur rang.
correction

2. Remplacer u_1, u_2, u_3 et u_n par les résultats obtenus précédemment dans l’égalité suivante  S=u_0+u_1+u_2+u_3+…+u_n.

correction

3. Après avoir mis u_0 en facteur dans le membre de droite et en utilisant la propriété n°3, exprimer   S=u_0+u_1+u_2+u_3+…+u_n en fonction de q et de n.

correction

Propriété n°4

On considère une suite géométrique de  raison q. On note S, la somme des n+1 premiers termes consécutifs de la suite (u_n), c’est-à-dire S=u_0+u_1+u_2+u_3+…+u_n.

On a S=u_0\frac{1-q^{n+1}}{1-q}

De façon plus générale :

S= premier \hspace{0.2cm} terme \times  \frac{1-raison^{nombre\hspace{0.2cm} de \hspace{0.2cm}termes}}{1-raison}

Remarque

La deuxième formule est plus générale, elle permet de calculer la somme de termes consécutifs d’une suite géométrique sans pour autant que le premier terme soit u_0.

Exemple n°1 

On veut calculer 1+2+4+8+16+32+64+128+256+512.

C’est une suite géométrique de raison 2.

La raison est 2.

Le premier terme u_0 est 1

Le dernier terme est 512, à l’aide de la calculatrice on l’écrit comme une puissance de 2 , 512=2^9. Il y a donc 10 termes.

1.Conjecturer avec la calculatrice TI-83 Premium

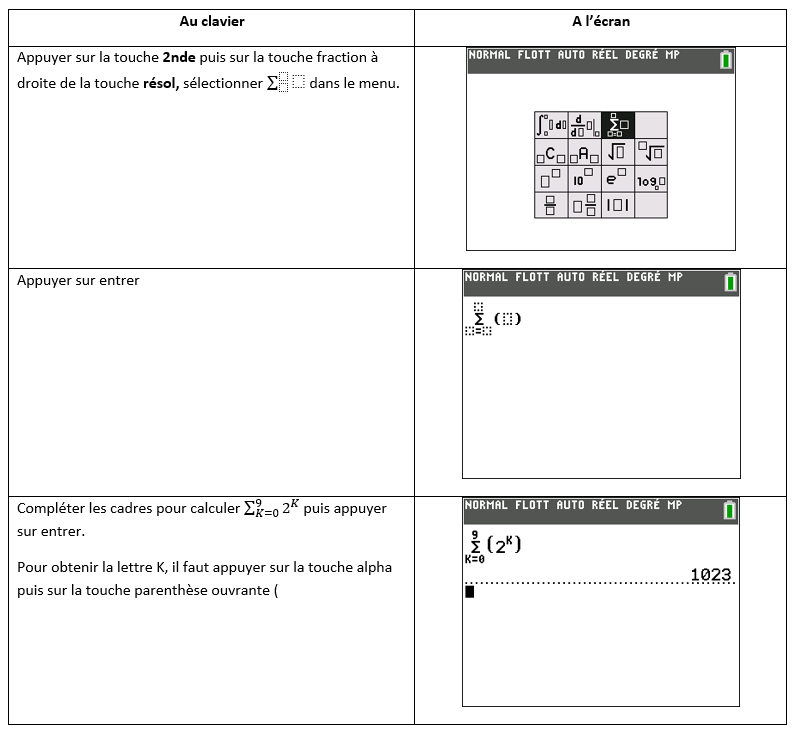
2.Conjecturer avec l’application Tableur de Géogébra.

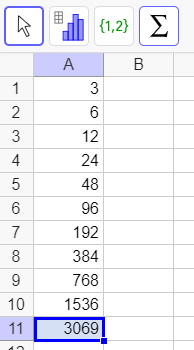
Saisir le premier terme est 1 dans la cellule A1.

Saisir la formule =A1*2 dans la cellule A2 et recopier vers le bas jusqu’à obtenir [latex512[/latex].

Sélectionner la plage allant de A1 à A10 et cliquer sur l’onglet \sum ( si ça ne marche pas du premier coup, recommencer). Parfois, il est plus facile de saisir dans la case vide qui suit le dernier terme =Somme(A1:A10).

On calcule à l’aide de la formule suivante :

S= premier \hspace{0.2cm} terme \times  \frac{1-raison^{nombre\hspace{0.2cm} de \hspace{0.2cm}termes}}{1-raison}

S=1\times\frac{1-2^{9+1}}{1-2}\\S=1\times\frac{1-2^{10}}{-1}\\S=\frac{1-1024}{-1}\\S=\frac{-1023}{-1}\\S=1023

Exercice n°3

Calculer les sommes suivantes composées de termes consécutifs d’une suite géométrique.

1.S_1=3+6+12+….+768+1536

correction

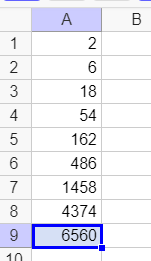
2.S_2=2+6+18+….+486+1458+4374

correction

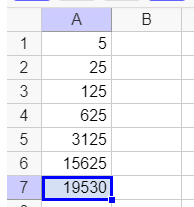
3.S_3=5+25+125+…+15625

correction

Exemple n°2 

(u_n) est une suite géométrique de premier terme u_0=5 et de raison  q=2.

On veut calculer S=u_0+u_1+u_2+…+u_8.

Conjecturer avec l’application Calcul Formel de Géogébra.

Saisir sur la ligne n°1 Somme(5\times 2^n,n, 0,8) et valider avec entrée. Le logiciel affiche la valeur 90

La raison est 2.

Le premier terme u_0 est 5.

De u_0 à u_8 il y a 9 termes.

On calcule à l’aide de la formule suivante :

S= premier \hspace{0.2cm} terme \times  \frac{1-raison^{nombre\hspace{0.2cm} de \hspace{0.2cm}termes}}{1-raison}

S=5\times\frac{1-2^{9}}{1-2}\\S=5\times\frac{1-512}{-1}\\S=5\times\frac{-511}{-1}\\S=5\times511\\S=2555

Exercice n°4

Calculer la somme S dans chaque cas.

  1. (u_n) est une suite  géométrique de premier terme u_0=\frac{1}{2} et de raison  q=2.

Calculer S=u_0+u_1+u_2+…+u_{12}.

correction

2. (u_n) est une suite géométrique de premier terme u_0=1 et vérifiant u_{n+1}=\frac{1}{2}u_n.

Calculer S=u_2+u_3+u_4+…+u_{15}.

correction

3. (u_n) est une suite géométrique définie par  u_n=2\times 0.1^n.

Calculer S=u_1+u_2+u_3+…+u_{20}.

correction

©2020 – Math’O karé SAS

On veut calculer la somme des 200 premiers nombres entiers non nuls :

S=1+2+3+…+100+101+…+198+199+200

1+200=201, je peux remplacer 1 par la moitié \frac{201}{2} et 201 par la moitié \frac{201}{2}. Cela ne change rien à la somme car 1+200=\frac{201}{2}+\frac{201}{2}.

S=\frac{201}{2}+2+3+…+100+101+…+198+199+\frac{201}{2}

2+199=201, je peux remplacer 2 par la moitié \frac{201}{2} et 199 par la moitié \frac{201}{2}. Cela ne change rien à la somme car 2+199=\frac{201}{2}+\frac{201}{2}.

S=\frac{201}{2}+\frac{201}{2}+3+…+100+101+…+198+\frac{201}{2}+\frac{201}{2}

3+198=201, je peux remplacer 3 par la moitié \frac{201}{2} et 198 par la moitié \frac{201}{2}. Cela ne change rien à la somme car 3+198=\frac{201}{2}+\frac{201}{2}.

S=\frac{201}{2}+\frac{201}{2}+\frac{201}{2}+…+100+101+…+\frac{201}{2}+\frac{201}{2}+\frac{201}{2}

On continue ainsi et enfin : 100+101=201, je peux remplacer 100 par la moitié \frac{201}{2} et 101 par la moitié \frac{201}{2}. Cela ne change rien à la somme car 100+101=\frac{201}{2}+\frac{201}{2}.

S=\frac{201}{2}+\frac{201}{2}+\frac{201}{2}+…+\frac{201}{2}+\frac{201}{2}+…+\frac{201}{2}+\frac{201}{2}+\frac{201}{2}

Il y a 200 fois écrit \frac{201}{2}, donc 

S=200\times \frac{201}{2}\\S=20100

On veut calculer la somme des 301 premiers nombres entiers non nuls.

S=1+2+3+…+151+…+299+300+301

1+301=302, je peux remplacer 1 par la moitié \frac{302}{2} c’est-à-dire 151   et 301 par la moitié \frac{302}{2} c’est-à-dire 151. Cela ne change rien à la somme car 1+301=151+151.

S=151+2+3+…+151+…+299+300+151

2+300=302, je peux remplacer 2 par la moitié 151 et 300 par la moitié 151. Cela ne change rien à la somme car 2+300=151+151.

S=151+151+3+…+151+…+299+151+151

3+299=302, je peux remplacer 3 par la moitié 151 et 299 par la moitié 151. Cela ne change rien à la somme car 3+299=151+151.

S=151+151+151+…+151+…+151+151+151

On continue ainsi et enfin, on arrive à la valeur centrale 151.

S=151+151+151+…+151+…+151+151+151

Il y a 301 fois écrit 151, donc 

S=301\times 151\\S=45451

On veut calculer la somme des p premiers nombres entiers non nuls :

S=1+2+3+…+…+(p-2)+(p-1)+p

1+p=1+p, je peux remplacer 1 par la moitié \frac{1+p}{2} et p par la moitié \frac{1+p}{2}. Cela ne change rien à la somme car 1+p=\frac{1+p}{2}+\frac{1+p}{2}.

S=\frac{1+p}{2}+2+3+…+(p-2)+(p-1)+\frac{1+p}{2}

2+(p-1)=1+p, je peux remplacer 2 par la moitié \frac{1+p}{2} et (p-1) par la moitié \frac{1+p}{2}. Cela ne change rien à la somme car 2+(p-1)=\frac{1+p}{2}+\frac{1+p}{2}.

S=\frac{1+p}{2}+\frac{1+p}{2}+3+…+(p-2)+\frac{1+p}{2}+\frac{1+p}{2}

3+(p-2)=1+p, je peux remplacer 3 par la moitié \frac{1+p}{2} et (p-2) par la moitié \frac{1+p}{2}. Cela ne change rien à la somme car 3+(p-2)=\frac{1+p}{2}+\frac{1+p}{2}.

S=\frac{1+p}{2}+\frac{1+p}{2}+\frac{1+p}{2}+…+\frac{1+p}{2}+\frac{1+p}{2}+\frac{1+p}{2}

On continue ainsi et enfin, il n’y a que des termes égaux à  \frac{1+p}{2}. Il y en a  p  au total, donc

S=p\times \frac{1+p}{2}\\S= \frac{p(1+p)}{2}

 

D’après le cours, u_n=u_0+nr. 

Et donc u_n+u_0=u_0+nr+u_0\\\hspace{2.3cm}=2u_0+nr

D’après le cours, u_1=u_0+r et u_{n-1}=u_0+(n-1)\times r

Et donc u_1+u_{n-1}=u_0+r+u_0+(n-1)\times r

On développe le produit (n-1)\times r

\hspace{2.7cm}=u_0+r+u_0+nr-r

On réduit le membre de gauche.

\hspace{2.7cm}=2u_0+nr

D’après le cours, u_2=u_0+2r et u_{n-2}=u_0+(n-2)\times r

Et donc u_2+u_{n-2}=u_0+2r+u_0+(n-2)\times r

On développe le produit (n-2)\times r

\hspace{2.7cm}=u_0+2r+u_0+nr-2r

On réduit le membre de gauche.

\hspace{2.7cm}=2u_0+nr

Dans les questions précédentes, on a vu que u_0+u_n ,  u_1+u_{n-1} , u_2+u_{n-2} sont tous égaux à 2u_0+nr.

En procédant comme Gauss, on peut donc remplacer chaque terme de la suite par la demi-somme suivante \frac{u_0+u_n}{2}.

Comme il y a n+1 termes de u_0  à u_n , la somme vaudra 

S=(n+1)\frac{u_0+u_n}{2}.

On conjecture le calcul de  15+16+17+…+57+58+59 à l’aide de l’application tableur de Géogébra. Comme il est compliqué de sélectionner toutes les cellules, on saisit =Somme(A1:A45) dans la cellule A46.

On veut calculer 15+16+17+…+57+58+59.

C’est une suite arithmétique de raison 1.

Le premier terme est 15

Le dernier terme est 59.

Pour trouver le nombre de termes on calcule : 59-15=44, on divise par la raison 1 :  \frac{44}{1}=44 et on ajoute le nombre 1  :  44+1=45. Il y a donc 45 termes.

On calcule

S=45\times \frac{15+59}{2}\\S=45\times \frac{74}{2}\\S=45\times 37\\S=1665

On vérifie avec la calculatrice TI-83 Premium :

On conjecture le calcul de  15+20+25+…+155+160+165 à l’aide de l’application tableur de Géogébra. Comme il est compliqué de sélectionner toutes les cellules, on saisit =Somme(A1:A31) dans la cellule A32.

On veut calculer 15+20+25+…+155+160+165.

C’est une suite arithmétique de raison 5.

Le premier terme est 15

Le dernier terme est 165.

Pour trouver le nombre de termes on calcule : 165-15=150, on divise par la raison 5 :  \frac{150}{5}=30 et on ajoute le nombre 1  :  30+1=31. Il y a donc 31 termes.

On calcule

S=31\times \frac{15+165}{2}\\S=31\times \frac{180}{2}\\S=31\times 90\\S=2790

On conjecture le calcul de  250+240+230+…+80+70+60 à l’aide de l’application tableur de Géogébra. Comme il est compliqué de sélectionner toutes les cellules, on saisit =Somme(A1:A20) dans la cellule A21.

On veut calculer 250+240+230+…+80+70+60.

C’est une suite arithmétique de raison -10.

Le premier terme est 250

Le dernier terme est 60.

Pour trouver le nombre de termes on calcule : 60-250=-190, on divise par la raison -10 :  \frac{-190}{-10}=19 et on ajoute le nombre 1  :  19+1=20. Il y a donc 20 termes.

On calcule

S=20\times \frac{250+60}{2}\\S=20\times \frac{310}{2}\\S=20\times 155\\S=3100

 (u_n) est une suite arithmétique de premier terme u_0=2 et de raison  r=3.

On veut calculer S=u_0+u_1+u_2+…+u_{12}.

Avant de commencer le calcul, on conjecture avec l’application Calcul Formel de Géogébra. 

Le premier terme est u_0, c’est-à-dire 2.

Le dernier terme est u_{12}=2+12\times 3=38.

De u_0 à u_{12} , il y a 13 termes.

On calcule à l’aide de la formule suivante :

S= nombre \hspace{0.2cm}de \hspace{0.2cm} termes \times  \frac{premier\hspace{0.2cm}terme \hspace{0.2cm} +\hspace{0.2cm} dernier \hspace{0.2cm}terme}{2}

S=13\times \frac{2+38}{2}\\S=13\times \frac{40}{2}\\S=13\times 20\\S=260

 

(u_n) est une suite arithmétique de premier terme u_0=-3 et vérifiant u_{n+1}=u_n+2.

On veut calculer S=u_2+u_3+u_4+…+u_{15}.

Avant de commencer le calcul, on conjecture avec l’application Calcul Formel de Géogébra. 

Attention : la forme explicite de (u_n) est u_n=-3+2n.

Saisir Somme(-3+2n,n,2,15) et faire entrée. Ici le logiciel a donné la réponse avec le symbole sigma vu précédemment.

Le premier terme est u_{2}=-3+2\times 2=1.

Le dernier terme est u_{15}=-3+15\times 2=27.

De u_2 à u_{15} , il y a (15-2)+1=14 termes.

On calcule à l’aide de la formule suivante :

S= nombre \hspace{0.2cm}de \hspace{0.2cm} termes \times  \frac{premier\hspace{0.2cm}terme \hspace{0.2cm} +\hspace{0.2cm} dernier \hspace{0.2cm}terme}{2}

S=14\times \frac{1+27}{2}\\S=14\times \frac{28}{2}\\S=14\times 14\\S=196

 

(u_n) est une suite arithmétique définie par  u_n=-1+5n.

On veut calculer S=u_1+u_2+u_3+…+u_{20}.

Avant de commencer le calcul, on conjecture avec l’application Calcul Formel de Géogébra. 

Saisir Somme(-1+5n,n,1,20) et faire entrée. 

Le premier terme est u_{1}=-1+5\times 1=4.

Le dernier terme est u_{20}=-1+5\times 20=99.

De u_1 à u_{20} , il y a (20-1)+1=20 termes.

On calcule à l’aide de la formule suivante :

S= nombre \hspace{0.2cm}de \hspace{0.2cm} termes \times  \frac{premier\hspace{0.2cm}terme \hspace{0.2cm} +\hspace{0.2cm} dernier \hspace{0.2cm}terme}{2}

S=20\times \frac{4+99}{2}\\S=20\times \frac{103}{2}\\S=10\times 103\\S=1030

 

On va multiplier cette égalité  S=1+q+q^2+q^3+…q^n par -q de chaque côté :

-q\times S=-q\times (1+q+q^2+q^3+…q^n)\\-q\times S=-q \times 1-q \times q  –  q \times q^2 –  q \times q^3 – …- q \times q^n\\-q\times S=-q-q^2-q^3-q^4-…q^{n+1}

 

On va ajouter cette égalité  S=1+q+q^2+q^3+…q^n et celle-ci: -q\times S=-q-q^2-q^3-q^4-…q^{n+1}.

\hspace{1.3cm}S=1+q+q^2+q^3+…q^n

\hspace{0.4cm}-q\times S=-q-q^2-q^3-q^4-…q^{n+1}

On ajoute.

S-q\times S=1+q+q^2+q^3+…q^n-q-q^2-q^3-q^4-…q^{n+1}

On réduit le membre de droite.

S-q\times S=1- q^{n+1}

On va mettre S en facteur dans le membre de gauche :

S(1-q)=1- q^{n+1}

Puis on exprime S en fonction de q et de n.

S=\frac{1- q^{n+1}}{1-q}

D’après le cours, u_1=u_0q,  u_2=u_0q^2,  u_3=u_0q^3 et u_n=u_0q^n.  

On remplace u_1 par u_0q, u_2 par u_0q^2, u_3 par u_0q^3 et u_n par u_0q^n dans  S=u_0+u_1+u_2+u_3+…+u_n.

S=u_0+u_0q+u_0q^2+u_0q^3+…+u_0q^n

S=u_0+u_0q+u_0q^2+u_0q^3+…+u_0q^n

On met u_0 en facteur dans le membre de droite.

S=u_0(1+q+q^2+q^3+…+q^n)

On remplace 1+q+q^2+q^3+…+q^n par \frac{1-q^{n+1}}{1-q} ( voir la propriété précédente)

S=u_0\frac{1-q^{n+1}}{1-q}

Conjecturons S_1=3+6+12+….+768+1536 à l’aide de la fenêtre Géogébra ci-dessous.

La raison est 2.

Le premier terme u_0 est  3

Le dernier terme est 1536, on le divise par le premier terme 3 et on obtient 512. A l’aide de la calculatrice on écrit 512 comme une puissance de 2 , 512=2^9.

1536=3\times 2^9 donc 1536=u_9 .

De u_0 à u_9 on a 10 termes.

On calcule à l’aide de la formule suivante :

S= premier \hspace{0.2cm} terme \times  \frac{1-raison^{nombre\hspace{0.2cm} de \hspace{0.2cm}termes}}{1-raison}

S=3\times\frac{1-2^{10}}{1-2}\\S=3\times\frac{1-2^{10}}{-1}\\S=3\times \frac{1-1024}{-1}\\S=3\times \frac{-1023}{-1}\\S=3\times 1023\\S=3069

 

 

Conjecturons S_2=2+6+18+….+486+1458+4374 à l’aide de la fenêtre Géogébra ci-dessous.

La raison est 3.

Le premier terme u_0 est 2

Le dernier terme est 4374, on le divise par le premier terme 2 et on obtient 2187. A l’aide de la calculatrice on écrit 2187 comme une puissance de 3 , 2187=3^7.

4374=2\times 3^7 donc 4374=u_7 .

De u_0 à u_7 on a 8 termes.

On calcule à l’aide de la formule suivante :

S= premier \hspace{0.2cm} terme \times  \frac{1-raison^{nombre\hspace{0.2cm} de \hspace{0.2cm}termes}}{1-raison}

S=2\times\frac{1-3^{8}}{1-3}\\S=2\times\frac{1-6561}{-2}\\S=2\times \frac{-6560}{-2}\\S=2\times \frac{6560}{2}\\S=6560

 

 

Conjecturons S_3=5+25+125+…+15625 à l’aide de la fenêtre Géogébra ci-dessous.

La raison est 5.

Le premier terme u_0 est 5

Le dernier terme est 15625, on le divise par le premier terme 5 et on obtient 3125. A l’aide de la calculatrice on écrit 3125 comme une puissance de 5 , 3125=5^5.

15625=5\times 5^5 donc 15625=u_5 .

De u_0 à u_5 on a 6 termes.

On calcule à l’aide de la formule suivante :

S= premier \hspace{0.2cm} terme \times  \frac{1-raison^{nombre\hspace{0.2cm} de \hspace{0.2cm}termes}}{1-raison}

S=5\times\frac{1-5^{6}}{1-5}\\S=5\times\frac{1-5^{6}}{-4}\\S=5\times\frac{1-15625}{-4}\\S=5\times \frac{-15624}{-4}\\S=5\times 3906\\S=19530

 

(u_n) est une suite  géométrique de premier terme u_0=\frac{1}{2} et de raison  q=2.

Conjecturons S=u_0+u_1+u_2+…+u_{12} à l’aide de la fenêtre Géogébra ci-dessous.

La raison est 2.

Le premier terme u_0 est  \frac{1}{2}

De u_0 à u_{12} on a 13 termes.

On calcule à l’aide de la formule suivante :

S= premier \hspace{0.2cm} terme \times  \frac{1-raison^{nombre\hspace{0.2cm} de \hspace{0.2cm}termes}}{1-raison}

S=\frac{1}{2}\times\frac{1-2^{13}}{1-2}\\S=\frac{1}{2}\times\frac{1-2^{13}}{-1}\\S=\frac{1}{2}\times\frac{1-8192}{-1}\\S=\frac{1}{2}\times\frac{-8191}{-1}\\S=\frac{1}{2}\times8191\\S=\frac{8191}{2}

 

(u_n) est une suite géométrique de premier terme u_0=1 et vérifiant u_{n+1}=\frac{1}{2}u_n.

A l’aide de Géogébra , conjecturons  S=u_2+u_3+u_4+…+u_{15}.

La raison est \frac{1}{2}.

Le premier terme u_2 est  u_0\times q^2=1\times (\frac{1}{2})^2 =\frac{1}{4}

De u_2 à u_{15} on a (15-2)+1=14 termes.

On calcule à l’aide de la formule suivante :

S= premier \hspace{0.2cm} terme \times  \frac{1-raison^{nombre\hspace{0.2cm} de \hspace{0.2cm}termes}}{1-raison}

S=\frac{1}{4}\times\frac{1-(\frac{1}{2})^{14}}{1-\frac{1}{2}}\\S=\frac{1}{4}\times\frac{1-\frac{1}{2^{14}}}{\frac{1}{2}}\\S=\frac{1}{4}\times2\times (1-\frac{1}{2^{14}})\\S=\frac{1}{2}\times \frac{2^{14}-1}{2^{14}}\\S= \frac{2^{14}-1}{2^{15}}\\S=\frac{16384-1}{32768}\\S=\frac{16383}{32768}

 

(u_n) est une suite géométrique définie par  u_n=2\times 0.1^n.

A l’aide de Géogébra, conjecturons la somme  S=u_1+u_2+u_3+…+u_{10}.

La raison est 0.1.

Le premier terme u_1 est  2\times 0.1^1=0.2

De u_1 à u_{10} on a (10-1)+1=10 termes.

On calcule à l’aide de la formule suivante :

S= premier \hspace{0.2cm} terme \times  \frac{1-raison^{nombre\hspace{0.2cm} de \hspace{0.2cm}termes}}{1-raison}

S=0.2\times\frac{1-0.1^{10}}{1-0.1}\\S=0.2\times\frac{0.9999999999}{0.9}\\S=0.2\times\frac{0.1111111111}{0.1}

On remplace 0.2 par \frac{1}{5} et on multiplie \frac{0.1111111111}{0.1} par 10000000000 en haut et en bas.

S=\frac{1}{5}\times \frac{1111111111}{1000000000}\\S= \frac{1111111111}{5000000000}

 

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.