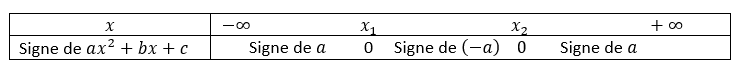Exercice n°1
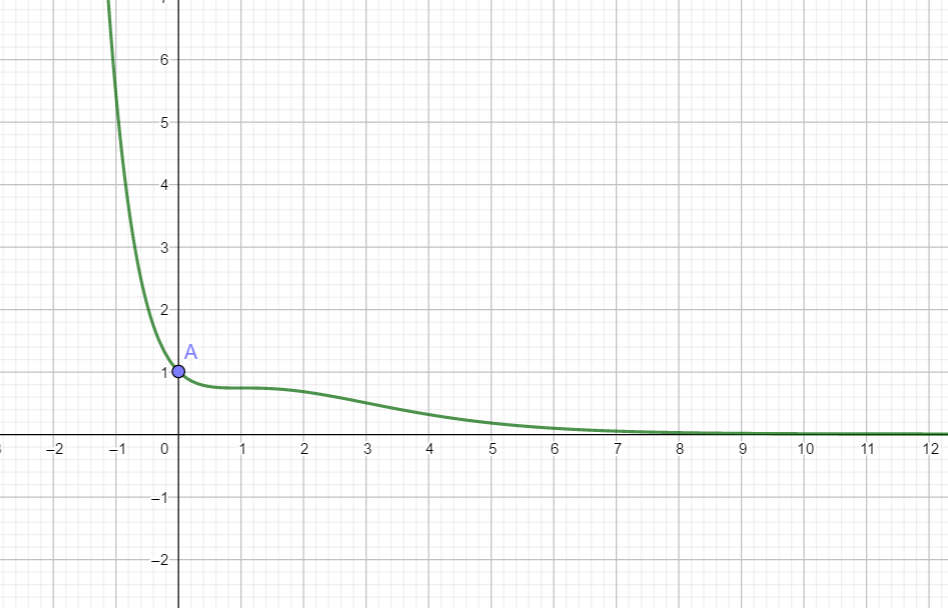
On considère la fonction f sur \mathbf{R} par f(x)=\frac{x^2+1}{e^x}
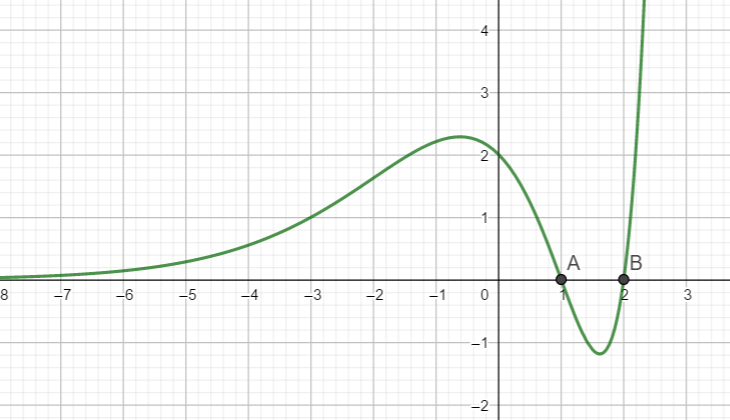
1. Déterminer les coordonnées du point A , point d’intersection de la courbe C_f avec l’axe des ordonnées.
2. La courbe C_f coupe-t-elle l’axe des abscisses ? Justifier la réponse.
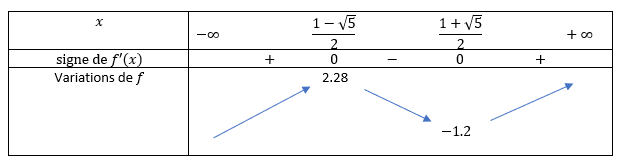
3. On note f’ la dérivée de la fonction f sur \mathbf{R} . Montrer que f'(x)=\frac{-x^2+2x-1}{e^x} .
4. Étudier le signe de f'(x)sur \mathbf{R} . En déduire le sens de variation de 𝑓 sur
\mathbf{R} .
5. On note T la tangente à C_f au point A d’abscisse 0. La tangente 𝑇 passe-t-elle par le point de (-6;8) ? Justifier la réponse.
Exercice n°2
On considère la fonction f sur \mathbf{R} par f(x)=(3x-3)e^x
1. Montrer que pour tout réel x , f'(x)=3xe^x .
2. Étudier le signe de f'(x) sur \mathbf{R} .
3. En déduire le tableau de variation de la fonction f sur \mathbf{R} .
4. Déterminer les coordonnées du point d’intersection de C_f avec l’axe des ordonnées, où C_f est la courbe de la fonction f.
5. Déterminer une équation de la tangente T à C_f au point d’abscisse 1.
Exercice n°3
Partie A
On considère la fonction g définie sur \mathbf{R} par :
g(x)=1-x+e^x.
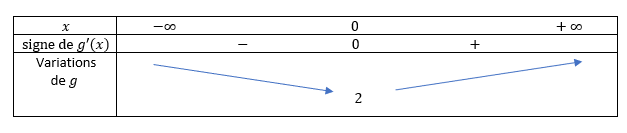
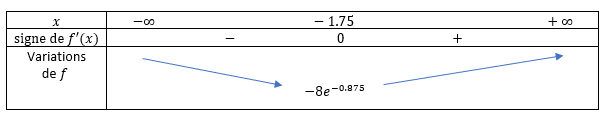
1) Montrer que g'(x)=e^x-1.
2) Résoudre e^x-1>0.
3) En déduire le tableau de variations de la fonction g définie sur \mathbf{R}. En déduire alors le signe de g(x).
Partie B
On considère la fonction f définie sur \mathbf{R} par :
f(x)=x+1+\frac{x}{e^x}
1) Calculer la dérivée f’ de f et vérifier que f'(x)=e^{-x}g(x).
2) Dresser le tableau de variations de la fonction f sur \mathbf{R}.
Exercice n°4
On considère la fonction f sur \mathbf{R} par f(x)=(x^2-3x+2)e^x
1. Montrer que pour tout réel x , f'(x)=(x^2-x-1)e^x.
2. Etudier le signe du polynôme suivant x^2-x-1 sur \mathbf{R} .
3. En déduire le tableau de variation de la fonction f sur \mathbf{R} .
4. Déterminer les coordonnées du ou des point(s) d’intersection de C_f avec l’axe des abscisses, où C_f est la courbe de la fonction f.
5. Déterminer une équation de la tangente T à C_f au point d’abscisse 1.
Exercice n°5
On considère la fonction f définie et dérivable sur \mathbf{R} par f(x)=(ax+b)e^{0.5x}où a et b
sont des réels fixés.
La courbe représentative C_f de la fonction f est donnée ci-dessous, dans un repère
orthogonal.
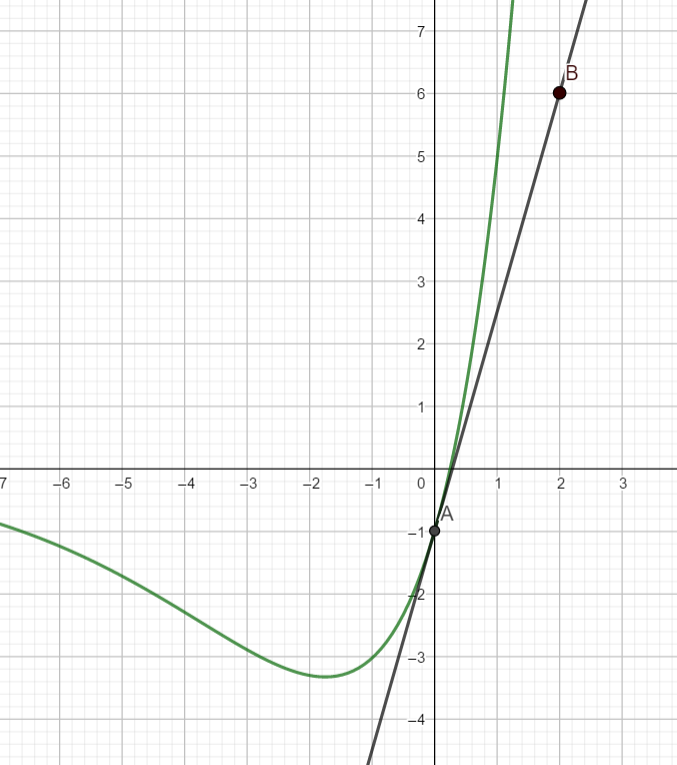
On a également représenté la tangente T à C_f au point A(0;-1) .
On admet que cette tangente T passe par le point B(2;6) .
1. En exprimant 𝑓(0), déterminer la valeur de 𝑏.
2. a) À l’aide des coordonnées des points A et B , déterminer une équation de la droite T .
b) Exprimer, pour tout réel x , f'(x) en fonction de x et de a et en déduire que pour tout réel x, f(x)=(4x-1)e^{0.5x}.
3. On souhaite déterminer le maximum de la fonction f sur \mathbf{R}.
a) Montrer que pour tout x \in \mathbf{R}, f'(x)=(2x+3.5)e^{0.5x}.
b) Déterminer les variations de f sur \mathbf{R} et en déduire le minimum de f sur \mathbf{R}.