Exercice n°1
ABC est un triangle tel que AB=6 , AC=4 et \widehat{BAC}=\frac{\pi}{3}. Alors \overrightarrow{AB}.\overrightarrow{AC}=
a) 12 | b) 12\sqrt{3} | c) 8 | d) 24 |
Exercice n°2
ABCD est un carré de centre O tel que AB=4. Alors \overrightarrow{AB}.\overrightarrow{CO}=
a) 6 | b) -8 | c) 0 | d) -6 |
Exercice n°3
\overrightarrow{u} et \overrightarrow{v} sont deux vecteurs orthogonaux tels que ||\overrightarrow{u}||=2 et ||\overrightarrow{v}||=3.
(2\overrightarrow{u}+3\overrightarrow{v}).(\overrightarrow{u}-2\overrightarrow{v}) est égal à :
a) -52 | b) 0 | c) -46 | d) 17 |
Exercice n°4
MNPQ est un losange de côté 6 et \widehat{NMQ}=\frac{\pi}{3}.
Alors \overrightarrow{MN}.\overrightarrow{MQ}=
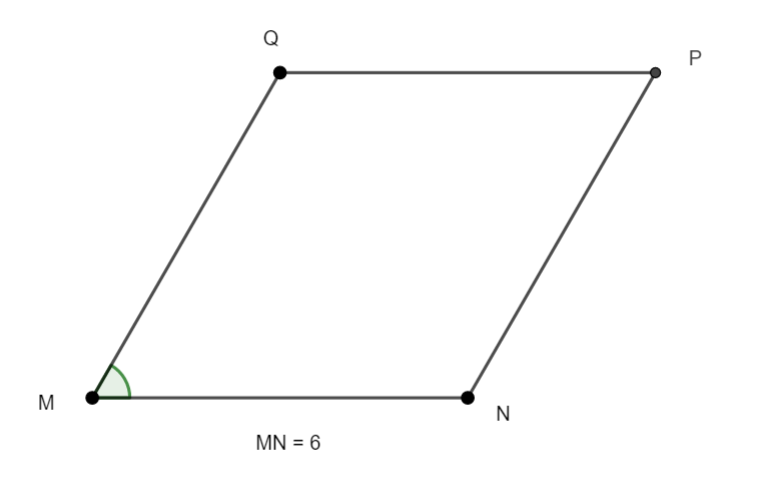
a) -36 | b) 36 | c) -18 | d) 18 |
Exercice n°5
ABC est un triangle tel que AB=6 , AC=4 et BC=5. Alors \overrightarrow{AB}.\overrightarrow{AC}=
a) -27 | b) -\frac{5}{2} | c) 0 | d) -\frac{27}{2} |
Exercice n°6
ABCD est un rectangle tel que AB=5 et
CB=3 .
Alors \overrightarrow{AC}.\overrightarrow{BD}=
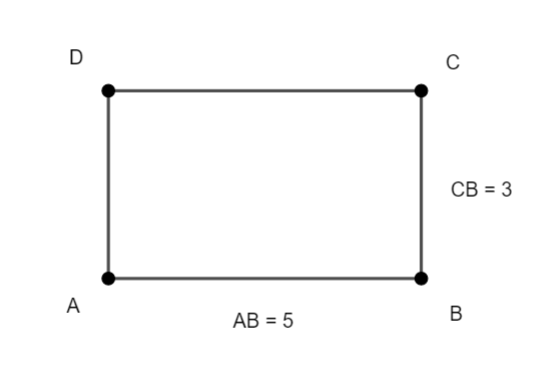
a) 0 | b) -16 | c) 2 | d) -2 |
Exercice n°7
A(1;2) , B(-1;2) et C(3;1).
Alors \overrightarrow{AB}.\overrightarrow{AC}=
a) -1 | b) -4 | c) -5 | d) 20 |
Exercice n°8
ABCD est un carré.
a) \overrightarrow{AB}.\overrightarrow{CD}=0 | b) \overrightarrow{AB}.\overrightarrow{AB}=0 | c) \overrightarrow{AC}.\overrightarrow{AD}=0 | d) \overrightarrow{AB}.\overrightarrow{AD}=0 |
Exercice n°9
Dans quel cas, \overrightarrow{AB}.\overrightarrow{AC}=15
a) AB=3 , AC=5 et BC=8. | b) A(4;7), B(1;2) et C(9;10). | c) ABC est rectangle en A, AB=3 et AC=5. | d) AB=3 , AC=5 et \widehat{BAC}=\pi |
Exercice n°10
\overrightarrow{AB}(2;-3) et \overrightarrow{AC}(3;-4).
Alors \overrightarrow{AB}.\overrightarrow{AC}=
a) -6 | b) -17 | c) 1 | d) 18 |
Exercice n°11
A(1;2) , B(5;-1) et C(-6;-2).
Alors \overrightarrow{AB}.\overrightarrow{AC}=
a) -40 | b) 40 | c) -16 | d) 16 |



